Упражнения_стр 86_87. 3 Отображения Упражнения

• Название: 3 Отображения Упражнения
• Дата: 04.04.2022
• Размер: 0.62 Mb.
• Имя файла: Упражнения_стр 86_87.docx
• Тип: Книга; #441749

3.2. Отображения

Упражнения

1. 
   Х- множество студентов в группе, Y- множество столов в аудитории. Каждому студенту соответствует стол, за которым он сидит. Является ли это соответствие отображением?
   
2. 
   Х- множество книг в данной библиотеке, Y- множество писателей. Является ли соответствие «Книга х написана писателем y» отображением?
   
3. 
   Между элементами множеств Х= {11,12,13,14,15,16,17} и Y= {0,1,2} задано соответствие «Число х при делении на 3 дает остаток у». является ли это соответствие отображением? Если да, то каким? Найдите полноценные прообразы для каждого элемента из Y.
   
4. 
   Х- множество пальто, висящих в гардеробе, Y- множество всех номерков в этом гардеробе. Каждому пальто соответствует номер крючка, на котором оно висит. Будет ли это соответствие отображением? При каком условии отображение будет обратимым?
   
5. 
   Докажите, что Множества Х и Y равномощны, если:
   
   1. 
      Х - множество букв в слове «таблица», Y - множество цифр числа 5484736;
      
   2. 
      Х - множество букв в слове «каравай», Y - множество букв в слове «молоток»;
      
   3. 
      Х - множество цветов радуги, Y- множество дней недели.
      
6. 
   Выделите из множества N_2k= {2,4,6,8,…,2n,…}два счетных подмножества, не совпадающих с N_2k.
   
7. 
   Х - множество точек отрезка АВ, Y - множество точек отрезка СD Докажите, что множества Х и Y равномощны (рис. 3.8, а).
   
8. 
   На рис. 3.8, б изображены две окружности. Х - множество точек первой окружности, Y - множество точек второй окружности. Докажите, что множества Х и Y равномощны.
   
9. 
   Докажите, что множество Х точек окружности и множество Y точек границы описанного треугольника равномощны (рис. 3.8, в).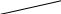
   

B

A



D

C




а б в

Рис. 3.8

10. 
    Являются ли отображениями следующие соответствия:
    
    1. 
       паре (a, b) ϵ N² соответствует число (a+b) ϵ N;
       
    2. 
       паре (a, b) ϵ N² соответствует число (a - b) ϵ N;
       
    3. 
       паре (a, b) ϵ N² соответствует число (a • b) ϵ N;
       
    4. 
       паре (a, b) ϵ N² соответствует число (a: b) ϵ N;
       
11. 
    Являются ли записанные ниже отображения биективными:
    
    1. 
       у=х³, где х ϵ R, y ϵ R;
       
    2. 
       у=х², где х ϵ R, y ϵ R;
       
    3. 
       у=3x-5, где х ϵ R, y ϵ R;
       
12. 
    Можно ли задать отображение следующим образом: множество Х состоит из отрезков, а множество Y- из треугольников; каждому отрезку составится в соответствие треугольник, для которого этот отрезок является средней линей. Ответ обоснуйте.
    
13. 
    Для того чтобы ввести понятие «столько же», учительница взяла несколько красных квадратов и на каждый из них наложила синий треугольник. Приведите теоретическое обоснование этого приема.
    
14. 
    Приведите примеры отображений из начального курса математики.
    

3.3Отношения на множестве и их свойства

Упражнения

1. 
   Отношение ρ на множестве Х задано с помощью графа (рис. 3.17, а). Пользуясь графом, среди следующих высказываний укажите истинные:
   
   1. 
      отношение ρ рефлексивно;
      
   2. 
      отношение ρ не является симметричным;
      
   3. 
      отношение ρ асимметрично;
      
   4. 
      отношение ρ не является транзитивным;
      
   5. 
      отношение ρ антитранзитивно.
      
2. 
   Какими свойствами обладает отношение, граф которого изображен на рис. 3.17, б?
   
3. 
   На множестве Х = {6, 7,8. 9, 10, 11, 12, 13, 14} задано отношение ρ-«иметь один и тот же остаток при делении на 3». Является ли оно отношением эквивалентности?
   

х


y





y

x



z



z


а б

Рис. 3.17

4. 
   На множестве Х = {1,2,8,9}задано бинарное отношение перечислением пар P={(1,1),(1,2),(2,1),(2,2),(1,8),(8,1),(8,8),(8,2),(2,8),(9,9)}. Докажите, что ρ - отношение эквивалентности. Постройте граф и график этого отношения, укажите их особенности. Выпишите классы, на которое разбивается множество Х.
   
5. 
   На множестве Х = {3, 6, 9.12, 15} задано отношение ρ -«х делится на у». Постройте граф и график этого отношения. Какими свойствами оно обладает? Упорядочивает ли оно множество Х?
   
6. 
   На рис. 3.18,а-в приведены графы отношений. Есть ли среди них граф отношения порядка?
   
7. 
   Используя граф бинарного отношения, решите следующие задачи.
   
   1. 
      На соревнования по прыжкам в длину класс выставил команду мальчиков. В нее входили Олег, Андрей, Максим, Игорь. Андрей прыгнул дальше Максима, но ближе Игоря. Максим прыгнул ближе Олега, а Олег ближе Андрея. Как распределились места на соревнованиях?
      
   2. 
      Олег, Дима, Толя, Миша и Петя - братья. Олег старше Пети, Дима моложе Толи, Петя старше Толи, а Миша моложе Пети. Кто из братьев старше: Олег или Миша? Петя или Дима? Можно ли утверждать, что Дима моложе Миши?
      

а б в

Рис 3.18

8. 
   В начальном курсе математики на множестве натуральных чисел рассматриваются отношения «больше», «больше на», «больше в… раз», «непосредственно следовать за», «число х делится на число у без остатка». Какие из этих отношений упорядочивают множество натуральных чисел?
   
9. 
   На множестве Х={7,8,9,10,11} задано отношение ρ- « Непосредственно следовать за». Постройте граф этого отношения. Какими свойствами оно обладает?
   

Аматова Г.М.

А612 Математика: в 2 кн. Кн. 1: учеб. Пособие для студ. высш. пед. Учеб. заведений/ Г.М. Аматова, М.А. Аматов. -М.: Издательский центр «Академия»,2008.- 256 с.

ISBN 978-5-7695-3999-2

c.86-87