Шпоры по матану [1 семестр]. Множество это совокупность элементов, понимаемых как единое целое (объединенных по некоторому признаку) Множество X
 Скачать 223 Kb.
|
|
Множество – это совокупность элементов, понимаемых как единое целое (объединенных по некоторому признаку) Множество X называется ограниченным, если существует число m такое, что для всех x X x m Если x m – ограничено сверху, x -m – ограничено снизу Верхней гранью множества X называется supp X такое, что x X x supp X и 0 x0 X x0 supp X - Нижней гранью множества X называется inf X такое, что x X x inf X и 0 x0 X x0 inf X + Точка A называется предельной точкой для множества X, если в любой ее проколотой окрестности существуют точки из множества X. Любой интервал, содержащий точку x0, называется окрестностью точки x0. Число a называется пределом последовательности Xn, если 0 такой номер N = N (), n N Xn - a Теорема. Если предел существует, то он единственный. Теорема. Если последовательность сходится, то она ограничена. Доказательство. lim (n) Xn = a N n N Xn - a Пусть = 1 M = max {X1, X2, ..., Xn, a + 1} Xn M n. m = min {X1, X2, ..., Xn, a - 1} Xn m n. Теорема. Если {Xn} монотонно возрастает, т.е. Xn+1 Xn n и ограничена сверху, то она имеет предел. Если {Xn} монотонно убывает, т.е. Xn+1 Xn n и ограничена снизу, то она имеет предел. Доказательство. Xn убывает, Xn+1 Xn n m m Xn Пусть m = inf {Xn} 1. n m Xn 2. 0 N XN m + lim (n) Xn = m 0 N n N m Xn XN m + m - Xn m + . Теорема о предельном переходе в неравенствах. Пусть lim (n) Xn = a и lim (n) Yn = b и пусть n Xn Yn, тогда a b. Доказательство. Пусть a b, = (a - b)/2 0. N1 n N1 b - Yn b + N2 n N2 a - Xn a + Пусть n max {N1;N2} a - Xn Yn b + a/2 + b/2 a/2 + b/2 (противоречие) Теорема о вложенных отрезках. Пусть есть система вложенных отрезков [a1;b1] [a2;b2] ... [an;bn] ... Тогда существует точка C, принадлежащая всем отрезкам. Доказательство. Последовательность a1, a2, ..., an убывает и n an b1, т.е. она имеет предел lim (n) an = a. Последовательность {bn} возрастает и bn a1, т.е. она имеет предел lim (n) bn = b. lim (n) (an - bn) = 0 = b – a, т.е. a = b C = a = b n an C bn, т.е. C принадлежит всем отрезкам. Пусть даны два множества D и G. Если каждому элементу множества D ставится в соответствие единственный элемент множества G, то говорят, что задана функция f: D G. Если D = R и G = R, то функция числовая, если D = N и G = R, то функция последовательность. Все функции, задаваемые с помощью знаков +, -, * и операцией взятия сложной функции от элементарных называются элементарными функциями. Предел функции. По Коши: Число a называется пределом функции f (x) при xx0 0 0 x 0 x – x0 f (x) - a . По Гейне: Число a называется пределом функции f (x) при xx0 {Xn}x0 f (Xn)a (n). Предел функции на бесконечности. 1. lim (xx0) f(x) = E 0 0 x 0 x – x0 f(x) E ( для + f(x) E, для - f(x) -E) 2. lim (x) f(x) = a 0 0 x x (для + x , для - x -) Односторонние пределы. Число a называется пределом слева (lim (xx0 - 0) f(x) = a), если 0 0 x x0 - x x0 f(x) - a Число a называется пределом справа (lim (xx0 + 0) f(x) = a), если 0 0 x x0 x x0 + f(x) - a Теорема. Если lim (xx0) f(x) = a , то функция ограничена в некоторой окрестности точки x0. Доказательство. Пусть = 1, тогда x 0 x - x0 a - f(x) a + Функция f(x) называется бесконечно малой в окрестности точки x0, если предел в этой же точке равен 0. Теорема. Сумма бесконечно малых функций есть бесконечно малая функция. Доказательство. lim (xx0) (x) = 0, lim (xx0) (x) = 0 /2 0 1 0 x 0 x – x0 1 (x) /2 /2 2 0 x 0 x – x0 2 (x) /2 x 0 x – x0 min (1,2) (x) + (x) lim (xx0) ((x) + (x)) = 0 Теорема. Если lim (xx0) f(x) = b 0, то функция 1/f(x) ограничена в некоторой окрестности точки x0. Доказательство. Пусть b 0, тогда = b/2 x 0 x – x0 f(x) - b b – f(x) b - f(x) b - f(x) = b/2 f(x) b/2 1/f(x) 2/b Теорема. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция. Доказательство. Пусть в окрестности точки x0 (x) M и lim (xx0) (x) = 0, тогда /M 0 0 x 0 x – x0 (x) /M 0 0 x 0 x – x0 (x) - (x) /M * M Теорема. Пусть lim (xx0) f(x) = b 0 и (x)(xx0) 0, тогда (x)/f(x) бесконечно малая функция в окрестности точки x0. Доказательство. 1/f(x) – ограниченная, *1/f(x) – бесконечно малая (по предыдущим теоремам). Пусть lim (xx0) f(x) = a и lim (xx0) g(x) = b, тогда:
Теоремы о предельном переходе в неравенствах. Теорема 1. Если x f(x) g(x), то lim (xx0) f(x) lim (xx0) g(x) Теорема 2. Пусть x из окрестности точки x0 (x) f(x) g(x) и lim (xx0) (x) = lim (xx0) g(x) = a, тогда lim (xx0) f(x) = a. Сравнение бесконечно малых функций. Функция (x) называется бесконечно малой более высокого порядка, чем (x) в окрестности точки x0, если lim (xx0) (x)/(x) = 0. Если бесконечно малые функции (x) и (x) имеют предел lim (xx0) (x)/(x) = k 0 , то (x) и (x) называют сравнимыми или одного порядка малости. Если k = 1, то (x) и (x) – эквивалентные бесконечно малые. Теорема. Сумма бесконечно малых функций эквивалента бесконечно малой низшего порядка. Доказательство. Пусть есть + + и - низшего порядка. /0 и /0, xx0 lim (xx0) + + / = lim (xx0) / + / + 1 = 1 + + Функция f(x) называется бесконечно большой в окрестности точки x0, если предел в этой точке равен / lim (xx0) f(x) = a Функция f(x) – бесконечно большая 1/f(x) – бесконечно малая. Для любых функций (x) и (x) с условием, что lim (xx0) (x)/(x) = 0, пишут (x) = ((x)) и говорят (x) о-малое (x), (x) = ((x)) (x) О-большое (x). Замечательные пределы.
Функция f(x) называется непрерывной в точке x0, если она определена в некоторой окрестности этой точки и lim (xx0) f(x) = f(x0) Теорема. Если функция f(x) и g(x) непрерывны в точке x0, то непрерывна функция f(x) g(x); f(x) * g(x); f(x)/g(x) (g(x) 0). Точки разрыва.
Функция f(x) называется непрерывной на замкнутом отрезке [a; b], если она непрерывна в каждой точке этого отрезка, а в точках a и b у нее существуют односторонние пределы. M – максимальное значение функции f(x) на отрезке [a; b], если x [a; b] f(x) M m – минимальное значение функции f(x) на отрезке [a; b], если x [a; b] f(x) m Теорема 1. Пусть f(x) непрерывна на отрезке [a; b], тогда она достигает свое наибольшее и наименьшее значение. Теорема 2. Пусть f(x) непрерывна на отрезке [a; b], тогда она принимает все значения между наибольшим и наименьшим значениями. m C M x0 [a; b] f(x0) = C Теорема 3. Пусть f(x) непрерывная на отрезке [a; b] принимает на концах этого отрезка значения разных знаков, тогда существует точка C [a; b] такая, что f(C) = 0. Теорема 4. Если в окрестности точки x0 функция y(x) монотонна, то у нее существует обратная функция, которая непрерывна, если непрерывна функция y(x). Производная. Производной функции f(x1) называется lim (f(x1 + x) – f(x1)) / x = f ’(x1) = lim (x0) f / x, где x = x2 – x1 – приращение аргумента, f = f(x2) – f(x1) – приращение функции. f / x = tg tg Назовем линию L касательной к кривой y = f(x) в точке x0, если для любой секущей, проходящей через x0 и x1, секущая будет стремиться к L при x1x0. tg - tg угла наклона касательной к кривой в точке x1 k = tg = f ‘ (x1) Правила дифференцирования.
Уравнение касательной: y – f(x0) = f ‘ (x0)(x – x0) Уравнение нормали: y – f(x0) = (- 1/f ‘ (x0))*(x-x0) Производная сложной функции. Пусть z = f(y) и y = (x) z = f((x)) z’x = lim (x0) z/x = lim (x0) z/ * /x = z’y * ’x z’x = z’y + ’x Производная обратной функции. Если функция у = f(x) и x = g(y) обратные, то y’x = 1/g’y. Доказательство. lim (x0) y/x = lim (g0) y/g = lim (g0, y0) 1/ (g/y) = 1/ g’y Таблица производных:
Функция  называется дифференцируемой в точке  если ее приращение  в этой точке может быть представлено в виде где   . Если приращение функции f = f(x) – f(x0) можно представить в виде A(x – x0) +(x – x0), то линейная часть A(x – x0) называется дифференциалом функции. Свойства дифференциала:
Доказательство. d(f +g) = (f + g)’dx = f’dx + g’dx = df + dg Теорема. Если функция имеет дифференциал, то она имеет и производную, причем A = f’(x0). Доказательство. Пусть функция имеет дифференциал f = A(x – x0) + (x - xo) f/x = A + (x - xo)/ x Пусть x0 f’(x0) = A df = f’(x0)dx С геометрической точки зрения дифференциал функции  равен приращению ординаты касательной к кривой  в точке  , когда аргумент получает приращение  Пусть имеется функция f((x)) = y. Найдем дифференциал. dy = (f((x)))’dx = f’ * ’(x) * dx = f’* d Последнее равенство называется свойством инвариантности дифференциала. Производные и дифференциалы высшего порядка Производная  определенная на некотором множестве  является также функцией от x. В случае ее дифференцируемости можно вычислить ее производную. Производная от производной  называется производной второго порядка: Аналогично  .Начиная с четвертого, порядок производной обозначается только индексом в скобках (сверху). Производные порядка 1–3 также обозначаются    По определению  В случае дифференцируемости производной   производная порядка n определяется равенством  (12) Дифференциал от дифференциала функции f в точке x (если функция определена и дважды дифференцируема) называется дифференциалом второго порядка:  Дифференциал n-го порядка функции (в случае дифференцируемости n раз,  ) определяется как дифференциал от дифференциала (n–1)-го порядка: Для вычисления дифференциала порядка n используют формулу:  (15) Дифференциалы второго и выше порядков не обладают (в отличие от дифференциалов первого порядка) свойством инвариантности, т. е. их форма, а следовательно и способ вычисления зависят от того, является ли аргумент x независимой переменной или дифференцируемой функцией другой переменной. Производная параметрической функции. Пусть функция задана параметрически, т.е. в виде x = x(t), y = y(t) Пусть у x существует обратная функция t = x (x), тогда y = y(x (x)) y’x = y’t (x (x))’ = y’t/x’t y’x = y’t/x’t Производная неявной функции. Если функция y = y(x) задана в виде (x,y) = 0, то говорят, что она задана неявно. Чтобы найти производную, выражение (x,y) = 0 дифференцируют по x, считая, что y = y(x), из получившегося ответа выражают y’. Теорема Ферма. Пусть в точке x0 функция f(x) имеет локальный максимум, т.е. f(x0) f(x) (имеет локальный минимум). Если функция f дифференцируема в точке x0, то f’(x0) = 0. Доказательство. Пусть x0 – максимум, f(x0) f(x) f(x) – f(x0)/(x – x0) 0, если x x0 Пусть xx0, по теореме о сохранении знаков неравенства имеем: f’(x0) 0 C другой стороны, если x x0: f(x) – f(x0)/(x – x0) 0 Пусть xx0 f’(x0) 0 Значит, 0 f’(x0) 0 f’(x0) = 0. Теорема Ролля. Если функция f(x) дифференцируема на отрезке [a; b] и f(a) = f(b) = 0, то существует точка C [a; b], где f’(C) = 0 Теорема Лагранжа. Пусть f(x) дифференцируема на отрезке [a; b], тогда существует точка C [a; b], такая, что f(b) – f(a) = f’(C) * (b - a) Теорема Коши. Пусть f(x) и g(x) дифференцируемы на отрезке [a; b], тогда существует точка C [a; b], такая, что f’(C)/g’(C) = (f(b) – f(a)) / (g(b) – g(a)). Неопределенностями считаются следующие выражения: 0*; 0 в степени ; в степени 0; 1 в степени и т.д. Правило Лопиталя. Пусть при вычислении lim (xx0) f(x)/g(x) получаются неопределенности. Если существует lim (xx0) f’(x)/g’(x), то он совпадает с lim (xx0) f(x)/g(x). Доказательство. Пусть имеется неопределенность 0/0. f(x0) = 0, g(x0) = 0 По теореме Коши: (f(x) – f(x0))/g(x) – g(x0) = f’(C)/g’(C) При xx0 Cx0 lim (xx0) f(x)/g(x) = lim (Cx0) f’(C)/g’(C). Условие возрастания и убывания функции. Если f’(x0) 0, то f возрастает в окрестности точки x0, если f’(x0) 0, то f убывает в окрестности точки x0. Доказательство. Пусть f’(x0) 0 f’(x) 0; x1 x2. f(x1) – f(x2) = f’(x3)(x1 – x2) f(x1) f(x2) f возрастает. Пусть f возрастает в окрестности точки x0. f/x = (f(x +x) – f(x))/ x 0, если x 0 или x 0. По теореме о предельном переходе в неравенствах имеем: f’(x0) 0. Точка  называется точкой локального максимума (минимума) функции , если существует некоторая окрестность точки такая, что для всех x из этой окрестности выполняется неравенство   .Значение  называется локальным максимумом (минимумом) функции.Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции. Теорема 3 (первый признак экстремума функции). Пусть – критическая точка непрерывной функции .Если в некоторой окрестности точки 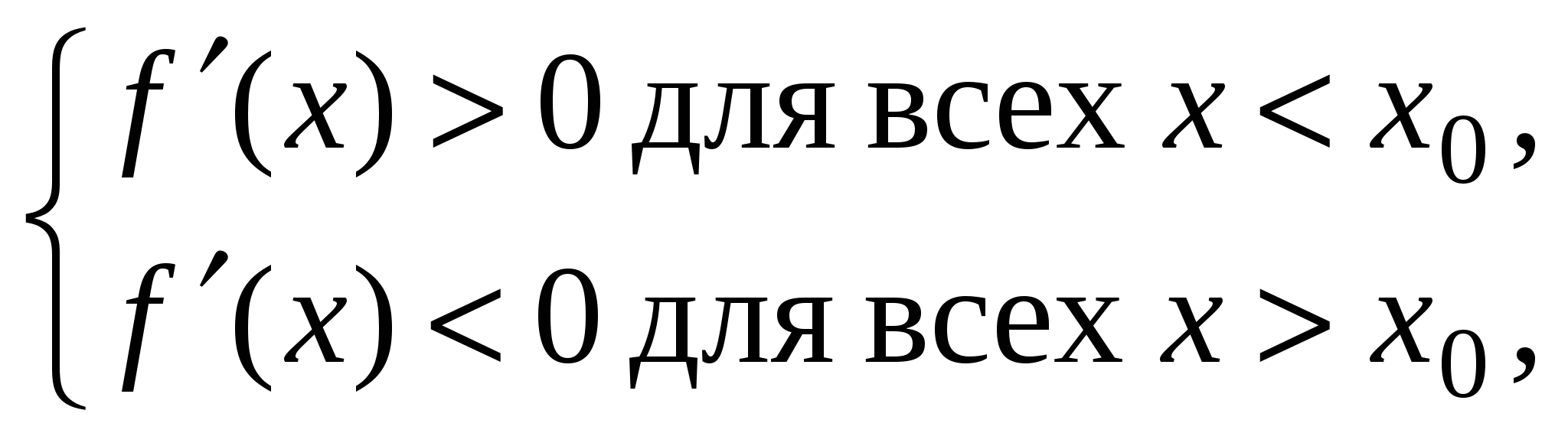выполняется условие то – точка локального максимума;если выполняется условие 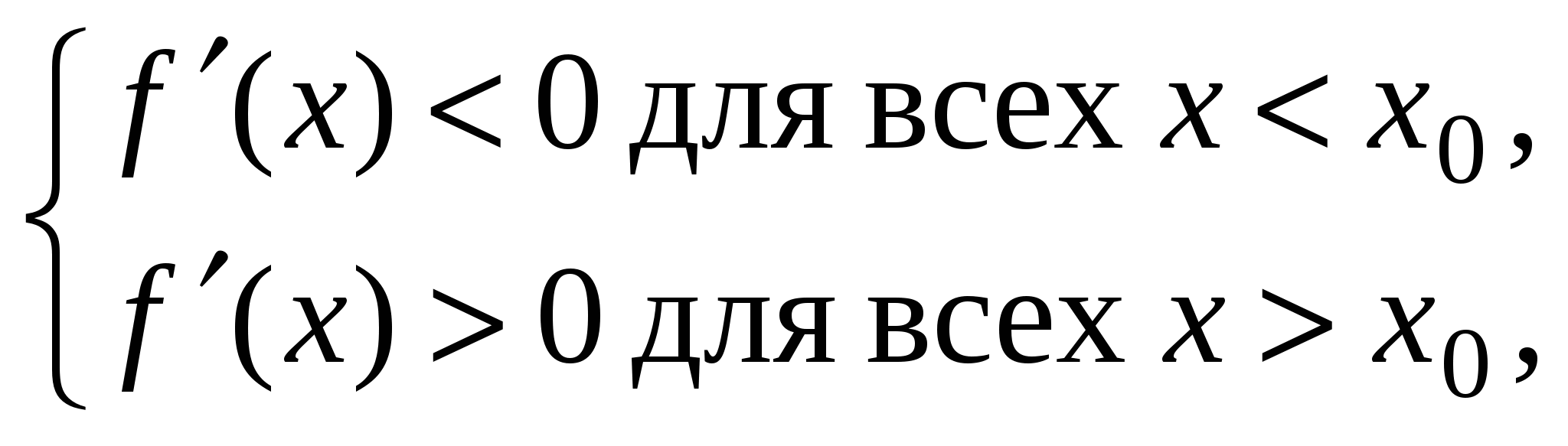 то – точка локального минимума.Если производная имеет один и тот же знак в левой и правой полуокрестности точки , то не является точкой экстремума.Теорема 4 (второй признак экстремума функции). Пусть – критическая точка функции , дважды дифференцируемой в окрестности точки . Тогда является точкой локального минимума функции , если  и точкой локального максимума, если  Теорема 5 (Вейерштрасса). Если функция непрерывна на отрезке  , то она достигает на нем своих наименьшего и наибольшего значенийНепрерывная на отрезке достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.Для отыскания глобальных экстремумов функции на отрезке необходимо:1) найти производную  2) найти критические точки функции; 3) найти значения функции на концах отрезка, т. е.  и  а также в критических точках, принадлежащих  4) из всех полученных значений функции определить наибольшее и наименьшее ее значения. Теорема о выпуклости графиков. Если функция f(x) дважды дифференцируема в окрестности точки x0 и вторая производная строго меньше нуля, то график функции выпуклый, а если больше нуля, то – вогнутый. Точка графика функции, в которой выпуклость сменяется вогнутостью (и наоборот) называется точкой перегиба. Асимптотой к графику функции y = f(x) называется прямая линия, расстояние от которой до графика стремится к нулю при неограниченном удалении точки графика от начала координат. План исследования функции и построения графика 1. Найти область определения  функции .2. Найти область значений  (если это возможно вначале, часто можно указать только по результатам исследования).3. Исследовать функцию на четность. 4. исследовать на периодичность. 5. Найти точки пересечения с осями Ox (нули функции) и Oy. 6. Найти промежутки знакопостоянства функции. 7. Исследовать на непрерывность, дать классификацию разрывов. 8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную). 9. Исследовать на монотонность и экстремум. 10. Исследовать на выпуклость, вогнутость, перегиб. 11. Построить график функции. На множестве X задана структура метрического пространства, если задана функция двух переменных, называемая метрикой, удовлетворяющая следующим аксиомам: (x; y) = (y; x); (x; y) = 0 y = x; x, y, z (x; z) (x; y) + (y; z). Множество D на плоскости назовем открытым, если оно содержит каждую свою точку вместе с некоторой окрестностью. Назовем точку z D предельной, если в каждой ее окрестности есть точки из множества D. Если множество D содержит все свои предельные точки, то оно называется замкнутым. Предел функции нескольких переменных. Число A называется lim (xx0,yy0) 0 -окрестность точки (x0; y0) (x; y) - окрестности (x x0 и y y0) f(x, y) - A . Непрерывность функции нескольких переменных. Функция z = f(x, y) называется непрерывной в точке (x0; y0), если она определена в окрестности этой точки и lim (xx0, yy0) f(x, y) = f(x0, y0) (по любому пути). Частные производные. Назовем частным приращением по x следующее выражение xf = f(x + x, y) – f(x, y) и частным приращением по y следующее выражение yf = f(x, y + y) – f(x, y). Частной производной по x называется lim (x0) xf/x = f/x (x, y) = f’x. Частной производной по y называется lim (y0) yf/y = f/y (x, y) = f’y. Если дифференцируемая функция принимает выражение f = f’yy +f’xx + (x, y) + (x, y), где /x²+y² 0 и /x²+y² 0, то выражение f’xdx + f’ydy называется полным дифференциалом функции f и обозначается df. Касательная плоскость. Касательная плоскость, проходящая через точку M0 некоторой поверхности имеет следующее свойство: угол между этой плоскостью и любой секущей MM0 (M плоскости) 0, при M M0. Уравнение нормали в каноническом виде: (x –x0)/ (f/x) = (y – y0)/ (f/y) = (z – z0)/ (f/z) Функция z = f(x, y) имеет локальный максимум в точке (x0, y0), если в окрестности этой точки значение f’(x – x0) f(x, y) (x, y). |