Тема Основные понятия и величины в гидравлике Предмет и методы гидравлики, основные характеристики жидкостей
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Тема 2. Основы теории потоков жидкостей и газов Виды и характеристики потоков. Под термином п о т о к в гидравлике в основном понимается одномерное течение жидкости под действием внешних сил. Поток считается одномерным, если его основные параметры – расход, скорость, давление – зависят только от одной координаты – вдоль потока (например, оси трубопровода). Течение может быть у с т а н о в и в ш и м с я (стационарным), если в рассматриваемом сечении потока его параметры не изменяются во времени, и н е у с т а н о в и в ш и м с я (нестационарным), если они, наоборот, зависят от времени процесса (например, при гидроударах). Важнейшей характеристикой потока является р а с х о д, то-есть количество жидкости, протекающее через сечение канала (трубопровода или струи) за единицу времени. Различают: - о б ъ е м н ы й расход Q = V/ t, м3/сек (2.1) и - м а с с о в ы й расход Qm = m/t, кг/сек. (2.2) Они связаны между собой соотношением Qm= ρQ . (2.3) C к о р о с т ь течения обычно считается равномерно распределенной по сечению потока и равной с р е д н е р а с х о д н о й скорости υ: υ = Q/ω, м/с, (2.4) где ω – площадь поперечного сечения потока.     Примечание. Физический смысл этой величины: скорость υ - это условно  постоянная по сечению потока скорость, υ и  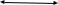 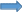 обеспечивающая такой же расход, что и действительная скорость течения (и), обычно переменная по сечению из-за  торможения потока на ограничивающих стенках канала (рис. 2.1). Рис. 2.1. Распределение скоростей Уравнение расхода (сплошности). При установившемся течении расход потока жидкости постоянен, хотя в отдельных сечениях скорость и давление могут меняться, в основном, из-за изменения площади проходного сечения. 9 1   2 Рис. 2.2. Схема    d1 d2 одномерного течения р1 Q р2 Из условия постоянства массового расхода Qm = constможно записать Qm1 = Qm2или ρQ1 = ρQ2. Ecли жидкость имеет постоянную плотность, то последнее уравнение можно записать так: υ1ω1 = υ2ω2, или 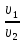 = =  , (2.5) , (2.5)то – есть, отношение скоростей потока обратно пропорционально отношению площадей сечений. Пример 2.1. Размеры конического трубопровода (рис. 2.2): d1= 100мм, d2 = 50 мм; расход жидкости Q = 10 л/с. Определить скорости потока на входе и выходе. Расчет. Средняя скорость на входе определится по ф. 2.4: υ1 = Q/ω = 4Q/πd12 = 4∙0,01/3,14∙0,12 = 1,27м/с. Скорость на выходе: υ2 = (ω1/ω2)υ1 = 4∙υ1 = 5,08 м/с. Уравнение Бернулли Уравнение Бернулли выражает закон сохранения энергии потока в напорной форме. Н а п о р – это удельная энергия потока, выраженная в метрах столба жидкости потока (например, в м. вод. ст.). Полный напор потока состоит из трех составляющих: - геометрический напор – Z; - пьезометрический напор -  ; - динамический (скоростной) напор - ; - динамический (скоростной) напор - 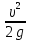 . . Полный напор потока идеальной (невязкой) жидкости при установившемся течении остается постоянным: Ho = Z +  + + 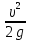 = const (2.6) = const (2.6)Примечание. Сумма двух первых слагаемых в ур. (2.6) наз. гидростатическим напором и выражает потенциальную энергию потока; последнее слагаемое – это кинетическая энергия. Следовательно, увеличение скорости должно вызывать снижение давления в потоке и наоборот. Допустим, что в примере 2.1 при течении воды (ρ = 1000 кг/м3) давление на входе р1 = 100 кПа; каким будет давление в сечении 2-2? Расчет: Из ф. (2.6) следует, что 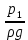 + +  = =  + + 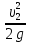 , то есть , то есть  = =  + + 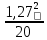 - - 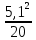 = = 8,78 м вод. ст. Значит, давление р2 = 87,8 кПа, т.е. оно уменьшилось по сравнению с давлением на входе. = = 8,78 м вод. ст. Значит, давление р2 = 87,8 кПа, т.е. оно уменьшилось по сравнению с давлением на входе.10 Скоростная трубка. Для измерения скоростного, динамического напора на практике применяется стандартный прибор – трубка Пито или скоростная трубка (рис. 2.3). Она включает два элемента: I– пьезометр, показывающий величину пьезометрического напора р/ρg, и II– трубка полного напора Но.            Разность уровней в трубках   Δh= υ2/2g, поэтому скорость  течения определится как ΔhII  υ = 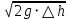 . (2.7) I . (2.7) I Рис. 2.3. υ Схема скоростной трубки Пример расчета. Если бы такие трубки были установлены в трубопроводе рис. 2.1, то показания их были бы: - на входе Δh1 = 1,272/20 = 8 см ; - на выходе Δh2 = 5,12/20 = 1,3 м. Расходомеры переменного перепада давления (РППД). Связь и взаимозависимость скорости и давления в потоке жидкости широко используется на практике в различных гидравлических устройствах и, в частности, в так наз. расходомерах переменного перепада давления (РППД). К ним относятся расходомерные диафрагмы, сопла и трубы Вентури. Рассмотрим принцип действия трубы Вентури (рис. 2.4).         d          Δр  υ1 υ1     р1 р2,υ2 D Рис. 2.4. Схема трубы Вентури ДМ Поток жидкости в трубе, движущийся в трубе диаметром Dсо скоростью υ1, сужается в горловине диаметром d, вследствие чего создается высокая скорость течения υ2 и возникает разность давлений Δр = р1 – р2. Эта 11 величина измеряется дифманометром ДМ и используется для определения расхода жидкости. Из уравнений Бернулли и сплошности получаем:  − − 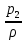 = = 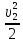 − −  ; ; 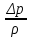 = = 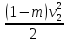 ; υ2= ; υ2=  ; Q =υ2∙ω2. ; Q =υ2∙ω2.Здесь: т = (d2/D2) – наз. модулем расходомера, который определяет степень сужения потока. Расчетная формула для расходомера: Q = A  , (2.8) , (2.8) где А – наз. постоянной расходомера; она определяется по формуле А = ω2  ). (2.9) ). (2.9) На практике часто используют Q тарировочные кривые (рис. 2.5), с помощью которых определяют расход жидкости по величине разности давления, измеряемой   дифманометром ДМ (способ реше- ния указан на рис. 2.5).  Рис.2.5. Δр  Тарировочная кривая расходомера Напорная диаграмма уравнения Бернулли                                   Напорная диаграмма – это график распределения напоров по длине трубопровода. На рис. 2.6 она приведена для потока идеальной жидкости.      Н Но 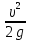 Линия полного напора Линия полного напора 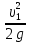 Пьезометрическая Пьезометрическая  линия  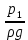 1 1  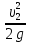  Рис. 2.6 Z12 Z Z2 12 |
