Билеты по ГА. Билеты по гидре хз хз хз. 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта

• Название: 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта
• Анкор: Билеты по ГА
• Дата: 12.04.2022
• Размер: 0.8 Mb.
• Имя файла: Билеты по гидре хз хз хз.doc
• Тип: Документы; #466442
• страница: 9 из 10

43 Оптимизация режима промывки скважины при турбинном способе

Возможности турбобура "принимать" нагрузку зависит от расхода Q. Следовательно, выбор Q зависит не столько от необходимости обеспечить удовлетворительную очистку забоя и ствола скважины, сколько от необходимости "обеспечить" забойный двигатель достаточным моментом М и мщностью N на валу турбобура. Дело в том, что М возрастает во второй степени от Q , а мощность – в третьей. По этой причине при турбинном бурении всегда присутствует естественное стремление промывать скважину при таких расходах, при которых рабочие давления на насосах близки к предельным (либо по втулкам, либо по прочности манифольда).

при роторном бурении, мы нашли, что на забое мощность гидромониторных струй будет максимальной, если выполнится условие: р_д = 2р_н/3.При турбинном бурении забойная гидравлическая мощность представлена мощностью N, передаваемой турбобуру. Следовательно, ничего не изменится в решении, если под р_д понимать перепад давления на турбобуре. Следовательно, турбобур разовьёт на забое максимально возможную мощность, если : или, что то же самое, . Но тут же возникает вопрос: как этого добиться?

Во-первых, необходимо стремиться к уменьшению потерь давления. Для этого следует, прежде всего, использовать бурильные трубы оптимального диаметра (см. подраздел 18,6): d_бт=(0.56…0.57)D_скв

Во-вторых, нужно определиться с числом секций турбобура. Необходимо взять такое число секций, при котором соотношение p_трб и p_н (или, что то же самое, соотношение p_пот и p_трб, которое должно быть, как 1:2) должно быть ближе к идеальному.

В третьих, нужно теперь увеличить Q, подобрав вариант числа одновременно работающих насосов и диаметров цилиндровых втулок, при котором давление p_н близко к p_доп. Только в этом случае на забое окажется гидравлическая мощность, близкая к 2/3 максимальной гидравлической мощности насосов. Только в этом случае будет завершена оптимизация режима промывки при турбинном бурении (только режима промывки, но не режима бурения в широком смысле этого понятия).

41.Расчёт линейных потерь давления при ламинарном течении «степенной» жидкости (ППЖ).

Реологическая модель псевдопластичной жидкости выражается уравнением: 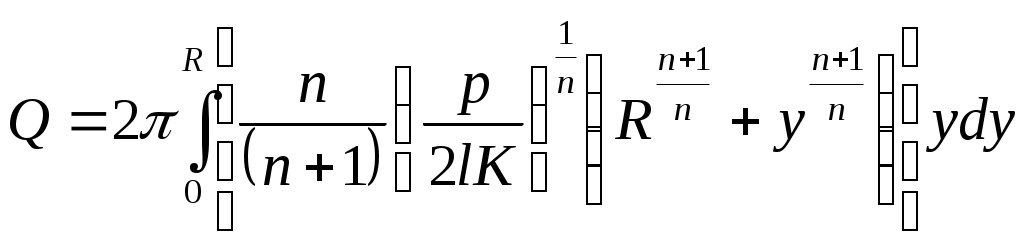. Реологическая функция: . Подставив это выражение в дифференциальное уравнение (4.10) и решив его в пределах изменения у от 0 до R, получим: При n= 1 это уравнение превращается в формулу (5.8). Для получения расчетной формулы необходимо составить уравнение расхода с использованием функции: . Интегрирование этого уравнения с последующей заменой R на d даст следующий результат: . После несложных преобразований: . При использовании v вместо Qформула примет вид: . Расчетные формулы, полученные на основе так называемой степенной реологической модели, не применимы при малых расходах, где они дают либо противоречащие здравому смыслу результаты, либо приводят к недопустимым погрешностям (в сторону завышения потерь). Пробные расчеты показали, что расход жидкости, соответствующий пересечению линий давления зависит преимущественно от диаметра труб: с уменьшением диаметра он тоже уменьшается.

Из анализа рис. 1 и 2 следует принципиально важный вывод об отсутствии логической связи между коэффициентом консистентности и динамической вязкостью вязкой жидкости, с которой сравнивается реологическое поведение псевдопластичной жидкости. Величина K не имеет физического смысла. Это не вязкость жидкости-прототипа, хотя и имеет размерность вязкости. Коэффициент К следует рассматривать только как коэффициент уравнения аппроксимации, полученного при реологических исследованиях. Одно и то же исследование может быть описано (с сопоставимыми показателями тесноты связи) различными комбинациями K и n, использование которых для определения потерь даст совершенно разные результаты, в том числе явно нелепые. Ясно, что такой результат отражает несовершенство уравнения (1), с помощью которого пытаются описать реологическое поведение жидкостей, называемых псевдопластичными.

Рис. 1. Изменение скорости по сечению потока степенной жидкости при одном и том же перепаде давления. Условия расчета: потери давления 1000 Па; длина трубы – 1000 м; диаметр трубы 200 мм; коэффициент консистентности 0,036 Па_*с.

Рис. 2. Зависимость потерь давления в трубе диаметром 200 мм и длиной 1000 м при движении псевдопластичной жидкости с параметрами по "степенной" модели: К=0,4Па*си различных значенияхn.

42. Критерии оптимизации гидромониторной промывки. Сила удара струи и гидравлическая мощность на долоте.

Известно несколько критериев оценки интенсивности струйной промывки забоя скважины, из которых наибольший интерес представляют [2]:

1. 
   скорость струй на выходе из насадкок v_ос;
   
2. 
   гидравлическая мощность струй на выходе из насадок (на долоте) N_o.заб;
   
3. 
   гидравлическая мощность струй в момент "встречи" с забоем N_заб;
   
4. 
   сила удара (количество движения) струй W_заб;
   
5. 
   осевое давление струи на забой скважины p_ос.
   

В настоящее время поиск оптимального варианта промывки скважины при бурении гидромониторными долотами осуществляется только по максимумам гидравлической мощности струй N_о.заб или силы их удара W_заб.

Логично предположить (в виде рабочей гипотезы), что положительный эффект от применения высокоскоростных гидромониторных струй пропорционален (или почти пропорционален) их суммарной мощности. Следовательно, можно утверждать, что из всех возможных вариантов промывки, отличающихся сочетанием Q, z_ни d_о, нужно выбрать такой, у которого мощность струй N_д=p_дQ максимальна.

Часть гидравлической мощности насосов N_н теряется на гидравлические потериN_пот=Р_потQ. Очевидно, что мощность, расходуемая на долоте N_д: N_д=N_нN_пот

Давление на насосах ограничено часто прочностью обвязки насосов p_доп= p_обв. Следовательно, гидравлическая мощность насосов равна: N_н=р_допQ.

Условимся, что во всех элементах циркуляционной системы имеет место квадратичный закон сопротивления: Р_пот=А_потQ². В результате имеем: N_д=р_допQА_потQ³. Принимая р_доп и А_пот постоянными, исследуем это уравнение на максимум N_д от Q, приравняв нулю первую производную по Q: р_доп-3А_потQ²= 0; Р_доп=3А_потQ²=3Р_пот; . Последнее равнозначно утверждению, что . Итак, гидромониторные струи обретут максимальную мощность, если перепад давления на долоте составит 2/3 от предельного давления на насосе, а оставшаяся 1/3 будет равна потерям давления. Q расход бурового раствора, м³/с;   плотность бурового раствора, кг/м³; p_д перепад давления на долоте, Па; d_п  диаметр подводящего канала долота (равный, как правило, входному диаметру насадок), м; l_с  расстояние от насадки до забоя (длина струи), м;z количество реально используемых в долоте насадок. Осевое давление струи р_ос, как критерий гидромониторной промывки, более технологичен. Оно количественно описывает воздействие струи на забой. Величиной осевого давления струи можно управлять, так как она зависит от расхода жидкости, диаметра насадок, длины струи, плотности жидкости и других факторов.

45 расчет линейных потерь давления при ламинарном течении вязкой жидкости (ВЖ)

При промывке скважины водой существование ламинарного режима в любoм из элементов циркуляционной системы практически невозможно, если иметь в виду реальные расходы Q. Вместе с тем применение вязких нефтей при освоении скважин или специальных жидкостей, например, при цементировании, делает существование ламинарного режима движения в трубах вполне возможным. Если в уравнение подставить реологическую функцию φ(τ)=τ/η, то получится решение: Подставив это уравнение в выражение и проинтегрировав его в пределах изменения y от 0 до R , получим известное решение Пуазейля-Гагена или, выразив расход через среднюю скорость, формулу .

Решение будет таким же, если воспользоваться формулой Дарси-Вейсбаха: , где .

46. 
    гидростатические давления в вертикальной и наклонно направленной скважинах
    

Наклонно направленная скважина, которая заполнена жидкостью, находящейся в покое в поле земного тяготения, 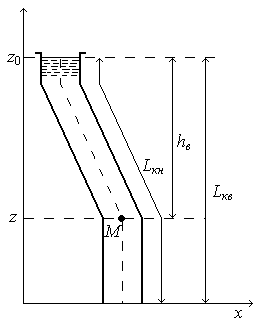показана на рис. 2.5. Когда массовые внешние силы представлены только силами тяжести, к жидкости, независимо от ее вида (вязкая или ВПЖ), можно применить основное уравнение гидростатики, в котором, как хорошо известно, нет координат xиy. Для точек (уровней) z_о и z (в точке М) это уравнение запишется в виде: или р=р_о+ρg(z_о-z)=p_о+ρgh_в, где h_в – погружение точки (уровня) М по вертикали. Вывод: давление столба жидкости на стенки наклонно направленной скважины зависит только от плотности жидкости и глубины скважины по вертикали. Пространственное положение ствола, следовательно, значения не имеет.

47 расчет линейных потерь давления при турбулентном течении вязкой жидкости

В случае вязких жидкостей рекомендуется воспользоваться решением А.Д. Альтшуля, который предложил формулу для коэффициента гидравлических сопротивлений : , где К_э - эквивалентная шероховатость. Эта формула справедлива как в переходной, так и в квадратичной области, поскольку при больших Re она практически превращается в формулу Шифринсона (ввиду малости второго слагаемого в скобках): .