Билеты по ГА. Билеты по гидре хз хз хз. 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта

• Название: 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта
• Анкор: Билеты по ГА
• Дата: 12.04.2022
• Размер: 0.8 Mb.
• Имя файла: Билеты по гидре хз хз хз.doc
• Тип: Документы; #466442
• страница: 3 из 10

11. Степенная жидкость. Её реограмма,параметры и реологическая функция.

Модель Освальда-де-Вале.Её реограмма,параметры и реологическая функция Это степенная модель. 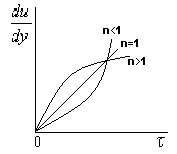_, - мера консистентности, Па·сⁿ; - показатель поведения (нелинейность),показывает на сколко отличается от прямой

12 Гидравлическая характеристика скважины

Под гидравлической характеристикой скважины обычно понимают представленные графически три зависимости :

• 
  изменение потерь давления р_к в заколонном пространстве от расхода Q;
  
  • 
    аналогичная зависимость потерь давления в циркуляционной системе в целом р_п (без учета перепадов давления на долоте и турбобуре, если последний имеется);
    
• 
  зависимость давления на насосе р_н от расхода Q .
  

Нет нужды доказывать, что вторая зависимость включает в себя первую, а последняя – вторую.

При использовании ВПЖ (рис. 12.1) зависимость р_к =f(Q) до достижения Q_кр будет практически линейной (линия 1). При Q > Q_кр (хотя бы на одном из участков кольцевого пространства) начнется турбулентный режим, и потери давления начнут расти быстрее, чем Q . В связи с тем, что _о >0 график р_к=f(Q) начинается не с нуля, а с p_о.к.

Сложнее обстоит дело с суммарными потерями давления в циркуляционной системе, включающими в себя потери в трубах, в кольцевом пространстве и манифольде (линия 2). Здесь невозможно говорить о типичности линии, отражающей зависимость р_п =f(Q) . Дело в том, что турбулентный режим внутри труб начинается, как правило, раньше, чем в затрубном пространстве; в УБТ – раньше, чем в бурильных трубах, а в манифольде, как уже отмечалось, режим движения всегда турбулентный. Для этой линии, которая всегда так же, как и предыдущая, начинается с р_о.п>0, характерна большая "квадратичность".

Если к потерям р_п добавить перепады давления р_ди р_трб(если турбобур введен в состав колонны труб), то получится линия 3, являющаяся гидравлической характеристикой скважины в целом. Обычно р_ди р_трб превышают существенно р_п .

Совершенно очевидно, что гидравлическая характеристика скважины постоянно меняется по мере углубления скважины. Иначе говоря, для каждой конкретной глубины имеется свой набор зависимостей р_к =f(Q), р_п =f(Q), р_н=f(Q). Иными становятся функции при существенном изменении технологических (особенно реологических и плотности ) параметров. Внесение изменений в компоновку бурильной колонны или изменение диаметра скважины немедленно отразится на гидравлической характеристике.

Очень полезно периодически "снимать" гидравлическую характеристику скважины при не менее чем трех (или более) фиксированных подачах насоса (насосов). Советуем не забывать при этом записать "остаточное" давление на

насосах (после остановки насосов, но до открытия пусковой задвижки). Величина р_о.пдает возможность оценить величину _о в реальных условиях бурения.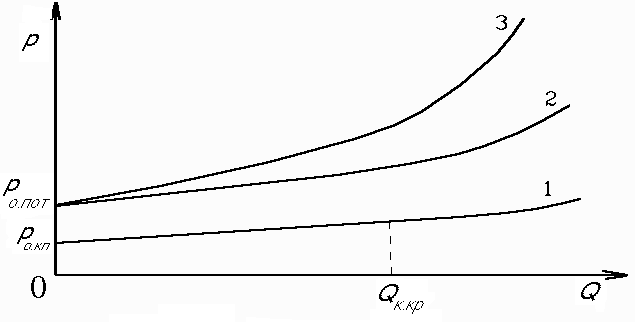



Рис. 12.1. Общий вид зависимостей р(Q) при промывке скважины вязкопластичной жидкостью: 1 – потери давления в заколонном пространстве; 2 – суммарные потери давления (сумма потерь в трубах и в заколонном пространстве); 3 – давление на насосах.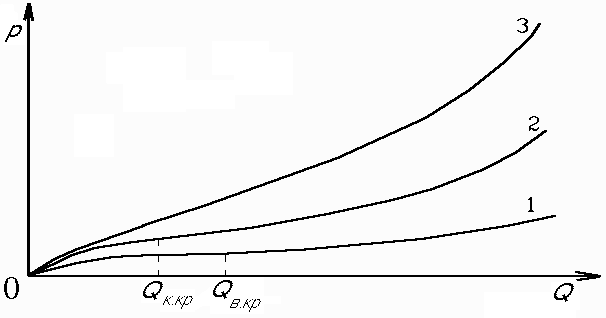



Рис. 12.2. Общий вид зависимостей р(Q) при промывке скважины псевдопластичной жидкостью: 1 – потери давления в заколонном пространстве; 2 – суммарные потери давления (сумма потерь в трубах и в заколонном пространстве); 3 – давление на насосах.Если жидкость при течении "подчиняется" псевдопластичной (степенной) модели (ППЖ), то гидравлическая характеристика будет заметно отличаться от таковой для ВПЖ (рис. 12.2). Как известно (об этом мы говорили в разделах 5 и 6), при ламинарном движении степенной жидкости, имеющей показатель нелинейности n<1, зависимость р =f(Q) будет соответствовать линии 1 (заколонное пространство) на рис. 12.2. Все линии, в том числе линия давления на насосе, берут начало в точке 0, поскольку ППЖ – не имеет начальной прочности (_о = 0) .

13. Основные реологические модели для буровых жидкостей.

Реологической моделью жидкости называется зависимость касательных напряжений _о от градиента скорости сдвига ỳ (или ). Реологические модели заданы уравнениями с определеными реологическими параметрами и отражают идеальное поведение реальных тел (табл.1).

В технической литературе по бурению для решения инженерных задач в области гидромеханики чаще других используется модель Шведова-Бингама (причина в том, что реологические параметры имеют четкую смысловую нагрузку):

Тем самым вводятся следующие допущения:

- буровые промывочные жидкости суть реологически стационарные системы, по крайней мере, становятся таковыми вскоре после начала движения;

- большинство буровых промывочных растворов, относящихся к аномальным жидкостям, удовлетворительно описываются моделью Шведова-Бингама.

Разумеется, не во всех задачах, не для всех жидкостей, применяемых в бурении, такие допущения корректны. В ряде случаев более точные решения могут быть получены с использованием степенных уравнений (модель Оствальда-де-Ваале или модель Кэссона-Шульмана), хотя, как только что было сказано, в области небольших градиентов скорости они вообще не применимы или приводят к недопустимым погрешностям.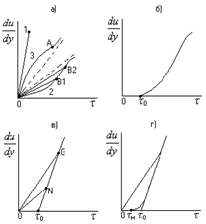



а – вязкая (ньютоновская) (1), псевдопластичная (2) , дилатантная жидкости(3); б – вязкопластичная жидкость (модель Кэссона-Шульмана); в - вязкопластичная жидкость (модель Бингама); г - вязкопластичная жидкость (модель Шведова);

Реологическая модель	Реологическое уравнение	Реологические параметры
Ньютона		- динамическая вязкость, Па·с
Шведова-Бингама		- динамическое напряжение сдвига, Па; - пластическая (структурная) вязкость, Па·с
Оствальда-де-Ваале		- мера консистентности, Па·сn; - показатель поведения (нелинейность)
Гершеля-Балкли		- динамическое напряжение сдвига, Па; - мера консистентности, Па·сn; - показатель поведения (нелинейность)

14.Гидравлическая характеристика буровых насосов

Гидравлическая характеристика насоса (насосов) – это зависимость между расходом (подачей насоса) и предельным давлением, которое может развить данный насосный агрегат.

Насосный агрегат может быть представлен одним, двумя и большим числом насосов (буровых, цементировочных и т.п.). Каждый насос или группа насосов имеет конкретную мощность привода (дизели, электродвигатели).

На рис. показана гидравлическая характеристика одного и двух буровых насосов У8-6М. В координатах "р_доп– Q" строго в масштабе нанесены гидравлические характеристики насосных агрегатов по их теоретической подаче (при коэффициенте наполнения _н, равном 1), а на них выделены точки (и линии), соответствующие разным диаметрам втулок (от 190 до 130 мм) расходы и предельно допустимые давления.

При использовании двух насосов, естественно, подача удваивается, но в обоих случаях насосный агрегат при указанных поршнях (втулках) не может развить давление более 14,3 МПа. Предел давления обусловлен установленной мощностью и механической прочностью поршневой группы и трансмиссии. Легко доказать, что произведение подачи на соответствующее предельно допустимое давление есть величина постоянная и по физическому смыслу равно установленной мощности (без учета размерностей):N =р_допQ

На рис. приведена гидравлическая характеристика насоса (насосов) У8-6М, которая представляет собой набор уже не точек, а горизонтальных отрезков прямых, "упирающихся" справа на соответствующую гиперболу. Дело в том, что дизельный привод позволяет (без существенного уменьшения выходного момента на валу дизеля) уменьшать подачу до 30…33%. Подача с уменьшением скорости вращения двигателя будет уменьшаться пропорционально этой скорости, но предельно допустимое давление останется без изменения (нельзя же превысить допустимую силу на поршень со стороны жидкости). Например, при втулках диаметром 170 мм один насос при дизельном приводе может качать от 23,6 до 35,6 дм³/с, а при двух насосах – два раза больше при одном и том же предельном давлении 14,3 МПа. Любопытно посмотреть, каким образом при дизельном приводе, например, обеспечить подачу Q=30 дм³/с. Оказывается, что таких вариантов пять (см. рис.10.3): 180, 170, 160, 140, и 130 мм.



15.Расход, скорость потока, средняя скорость потока в трубах, заколонном пространстве, желоба.



Это уравнение носит имя Букингэма (расхода ВПЖ), и было получено им в 1921 году.

Вэтом уравнении искомая величина потерь давления p не может быть в явном виде выражена через другие. Если задаваться расходом Q и другими параметрами (l, R, , _o ), то величину p можно вычислить численным методом. В уравнении (4.20) величина p_o определяется предварительно по формуле (4.6). Если подставить (4.6) в уравнение (4.20), то получим: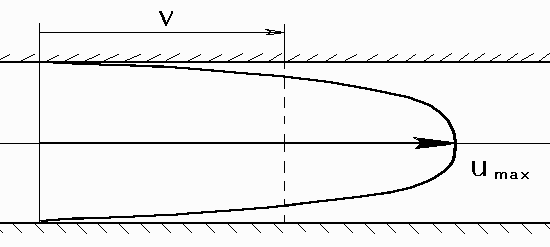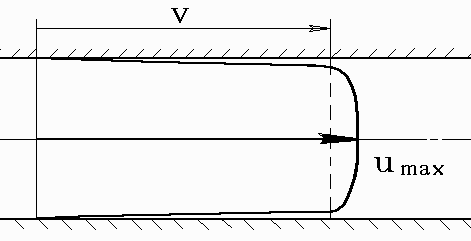



(4.6) Распределение скоростей по сечению потока. Речь идет о закономерности распределения скорости вдоль радиуса трубы, в сечении, проведенным перпендикулярно потоку. В осесимметричных каналах распределение скоростей можно изобразить эпюрой скоростей. В центре потока скорость u_o максимальна, а на границе со стенками (вследствие гидрофильности жидкости) скорость равна нулю. Эпюра скоростей при ламинарном течении вязкой жидкости (pиc. 1) существенно отличается от таковой при турбулентном движении (рис. 2) .
Средняя скорость потока v.

В расчетной практике удобнее иметь дело не со скоростями, переменными по сечении (эпюрой скоростей), а со средней по сечению скоростью. Нетрудно догадаться, что средняя скорость v равна длине образующей цилиндра, объем которого равен объему тела вращения, образованного эпюрой скоростей.

Чтобы измерить среднюю скорость потока, необходимо объем жидкости, прошедшей через данное сечение в единицу времени, Q разделить на площадь поперечного сечения потока (основания пространственной эпюры скоростей) f:v = Q / f

16. Распределение касательных напряжений по радиусу потока при движениии жидкости в трубах

Рассмотрим состояние динамического равновесия цилиндрического объёма жидкости, двигающегося равномерно по трубе под действием перепада давления р=р₁–р₂ (рис.). Сила внешняя, поддерживающая движение жидкого цилиндра длиной l и радиусом у, равна y².Сила сопротивления сосредоточена на внешней поверхности цилиндра и является результатом возникновения касательных напряжений из-за разницы скоростей движения различных слоев на радиусе y. Величина этой силы равна произведению поверхности цилиндра на его длину: 2yl. При равномерном движении обе силы равны:y²p = 2yl, yp = 2l,  p = 2yl . (4.1) При y = R (на стенке трубы)  =_R. Тогда . (4.2) Из уравнения (2.1.) следует, что . (4.3) При y = 0 = 0, а при y = R = _R. Из формулы (4.3.) следует, что зависимость касательных напряжении от расстояния y имеет линейный характер, причем, на самой оси напряжение равно нулю. Эпюра напряжений для круглых труб показана на рис. 4.1. Из неё видно, что справедливо соотношение . Следовательно, или . Если бы существовали методы определения _R (касательных напряжений на стенке трубы), то по формуле (4.2) можно было бы вычислить линейные потери давления при ламинарном движении любой жидкости в круглых трубах. К сожалению, такое невозможно, что вынуждает нас продолжить поиск расчетной формулы.

17. Расчет пусковых и остаточных давлений

Расчет сводится к решению задачи: какое давление нужно создать в спущенных в скважину трубах, чтобы вывести вязкопластичную жидкость, которой заполнены трубы и скважина, из состояния покоя. 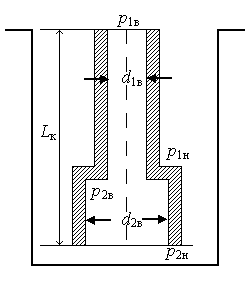Показанная на рис. 2. система труб представляет собой систему сообщающихся сосудов, один из которых образован стенками скважины и наружными стенками труб, а другой – самой трубой. Примем, что колонна труб состоит из секций труб двух размеров d₁ и d₂. Длина секции соответственно l₁ и l₂. Диаметр скважины – D. Длина колонны – L_к. Внутренний диаметр труб d_1в и d_2в.

Усложним задачу. Договоримся, что колонна труб заполнена жидкостью с ρ_в, θ_в, а заколонное – с параметрами ρ_кп, θ­_кп, причем ρ_кп>ρ_в. Такая ситуация создается, например, в конце цементирования обсадной колонны, когда в кольцевом пространстве за трубами находится еще не начавший застывать цементный раствор, а в колонне – продавочная жидкость.

Условие предельного равновесия вязкпластичной жидкости в этом случае запишется следующим образом.

р_о(р_1в+р_2в+р_1н+р_2н)(ρ_кпρ_в)gL=0,

где р_о – "пусковое" давление;

р_1в и р_2в – давления, необходимые для преодоления сил, вызванных напряжениями θ в трубах;

р_1н и р_2н – то же для заколонного пространства.

Последний член уравнения – это давление, необходимое для уравновешивания давления, вызванного разной плотностью жидкости в трубах и в заколонном (затрубном) пространстве.

Определим давления р_1в, р_2в, р_1н и р_2в: ;
. Аналогично для второй секции: ; . Подставив эти выражения в уравнение, найдем р_о: . При i –том числе секций: . В частном случае – в процессе бурения – когда ρ_в=ρ_кп=ρ, θ_в=θ_кп=θ, получим формулу:

. Для практики бурения представляет большой интерес и другая задача, обратная рассмотренной: определение "остаточного" давления на насосах р_ост после того, как насосы плавно остановлены без открывания пусковой задвижки. Дело в том, что при этом давление на насосах никогда не опускается до нуля сразу. Если считать, что жидкость подчиняется модели Бингама, то будет справедливо признать, что в данном случае р_ост является величиной, эквивалентной не θ, а τ_о. , Сравнение θ и τ_о даст оценку степени реологической нестационарности применяемой промывочной жидкости.


18. Ротационные вискозиметры. Схема и порядок проведения замеров.

График зависимости называется реологической кривой или реограммой. Приборы, предназначенные для получения реологических кривых (реограмм) и реологических констант называют вискозиметрами. Наибольшее распространение получили ротационные вискозиметры в силу их простоты конструкции и эксплуатации.

Приборы, предназначенные для измерения реологических свойств аномальных жидкостей, часто называют (в отличие от вискозиметров для ньютоновских жидкостей) пластомерами или реометрами (капиллярные вискозиметры).

В реологии буровых промывочных жидкостей широко применяются ротационные вискозиметры, в частности, вискозиметр ВСН-3 (безнадежно морально устаревший). Прибор представляет собой цилиндрический сосуд, в который соосно помещается другой цилиндр, образующий кольцевой зазор с первым. В этот зазор помещается испытуемая жидкость. Внутренний цилиндр подвешивается на упругой нити (пружине). Внешний цилиндр может вращаться с различной скоростью (дискретно). В кольцевом зазоре, в находящейся в нем жидкости возникают сдвиговые деформации при известном градиенте скорости (поскольку известна окружная скорость движения внешнего цилиндра по отношению к внутреннему цилиндру ∆u и известен размер зазора ∆у). Силы внутреннего трения передаются внутреннему цилиндру, возникает вращающий момент, пропорциональный величине τ, приводящий к закручиванию упругой пружины на угол φ, являющийся мерой τ. Изменение частоты вращения п сопровождается изменением φ.

19. Реограммы буровых жидкостей, реологические параметры.

Экспериментально полученный график зависимости 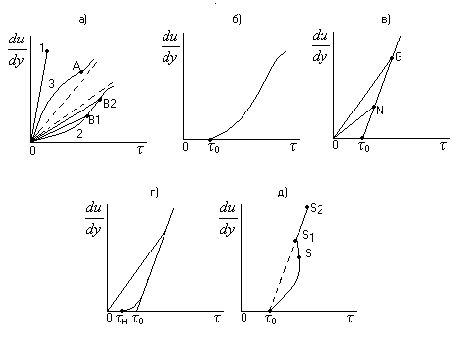называется реологической кривой или реограммой. Жидкости, в которых при постоянной скорости деформации напряжения сдвига уменьшается во времени называются тиксотропными. К наиболее распространенным тиксотропным системам относятся глинистые суспензии, тампонажные цементные растворы. Реограммы буровых жидкостей относятся к: 1. псевдопластичной ("степенной") реологической модели жидкости Оствальда-де-Ваале и соответствуют уравнению . Псевдопластичные жидкости характеризуются эффективной вязкостью η_эф ,которая увеличением градиента скорости сдвига уменьшается, - мера консистентности, Па·сⁿ; - показатель поведения (нелинейность).Установлено, что буровые растворы, обработанные полимерами, приобретают свойства псевдопластичной жидкости. Для данной модели характерно отсутствие начальной прочности τ_о.



Рис. В.1. Реограммы реологически стационарных жидкостей:

а – вязкая (ньютоновская) (1), псевдопластичная (2), дилатантная жидкости; б – вязкопластичная жидкость (модель Кэссона-Шульмана); в - вязкопластичная жидкость (модель Бингама); г - вязкопластичная жидкость (модель Шведова); д – тиксотропно-вязкопластичная жидкость. 2. вязко-пластичной реологической модели Кэссона-Шульмана: (В.4) Если реограмма представляет собой прямую (рис. В.1в), то такая жидкость называется жидкостью Бингама. Математически модель определяется уравнением: . (В.5) Шведов показал, что часть жидкостей ведет себя в соответствии с реограммой, показанной на рис. В.1г. Как видим, она состоит из двух участков: кривой (подобно модели Кэссона-Шульмана) и прямой, схожей с моделью Бингама. Для характеристики реограммы Шведова необходимо и достаточно знать три параметра: τ_н, τ_о и η. Заметим, что для модели Бингама достаточно знать τ_о и η. Обычно криволинейной частью реограммы Шведова пренебрегают, и тогда модель превращается в модель Бингама. В итоге как бы объединяются две модели в одну Шведова-Бингама. Где η-пластическая вязкость Па*с, τ_о -динамическое напряжение сдвига Па.

3.Ньютоновской (вязкой) модели жидкости. Из формулы следует, что μ – это сила трения, приходящаяся на единицу поверхности трения, при градиенте скорости равном единице (динамическая вязкость). Для того чтобы жидкость полностью подчинялась ньютоновской модели, необходимо, чтобы величина μ не зависела от градиента скорости du/dy. Это, в частности, означает, что с увеличением скорости жидкость и не разжижается, и не становится более вязкой. Зависимость в таких случаях графически изображается в виде прямой, исходящей из начала координат.

4.Можно выделить еще одну модель – так называемую тиксотропно-вязко-пластичную жидкость, типовая реограмма которой показана на рис. В.1д.

Прочность их зависит от времени. Находясь в покое, глинистый раствор упрочняется, в нем происходит процесс восстановления связей между коллоидными частицами. Под влиянием взаимодействия частиц дисперсной фазы между собой и молекулами дисперсной среды в системе образуется структура.

20. Анализ уравнения Букингема. Вывод формулы Бингама. 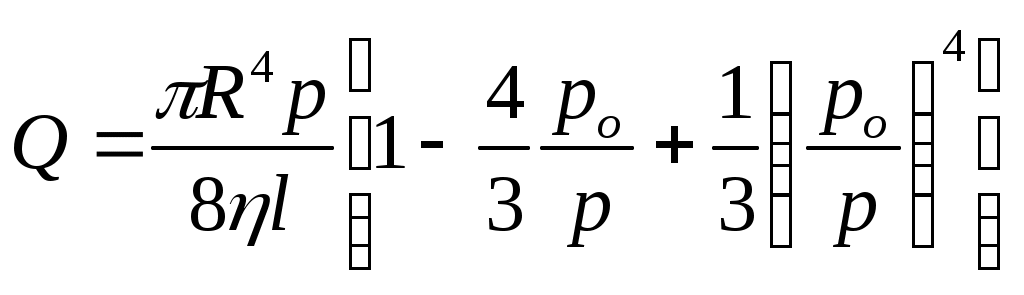уравнение Букингэма.При p_o=0 уравнение превращается в известную формулу Пуазейля-Гагена. При р_о/р=0,5 третий член уравнения равен 0,0208. Это означает, что его роль едва превышает 2%. Очевидно, при p 2p_o третьим членом уравнения Букингэма можно пренебречь и представить его в "усеченном" виде: . (5.1)

Заменим р_о на выражение (4.6): . Выразим р через другие параметры: . Заменим R на диаметр канала труб d: . (5.2)

Эта формула носит имя Бингама. Если вместо Q пользоваться средней скоростью v, то получим вариант формулы Бингама: , (5.3) где первый член формулы подставляет собой формулу Пуазейля-Гагена.

21. Профиль скоростей при турбулентном режиме движения и его роль при

замещении одной жидкости другой.

Экспериментальное и теоретические исследования показывают, что в переходной области профиль скорости явно зависит от числа Re. Считается, что профиль скорости может быть описан степенным уравнением : , (6.6) где u_max - максимальная скорость в центре потока (рис. 6.1);

u – скорость на радиусе у;

ε – величина, зависящая от Re, изменяется в пределах от 6 до 10.

При Re<10⁵ величину ε можно принять равной 7 .

В


Рис. 4.1. Эпюра скоростей при ламинарном и турбулентном режимах движения жидкостей в трубе

сравнении с ламинарным движением турбулентный режим является более предпочтительным, так как обеспечивает несравненно более выравненную эпюру скоростей по радиусу трубы , соответствующую формуле (6.6). Только у стенки трубы наблюдается резкое уменьшение скорости u. Следовательно, при турбулентном движении достигается хорошее вытеснение с минимальной длиной зоны смешения. Иначе говоря, если есть реальная возможность с помощью насосов поддерживать расход Q, превышающий Q_кр, то следует процесс замещения проводить при турбулентном режиме, а не при ламинарном.

22. Достоинства и недостаткиротационных и капиллярных вискозиметров.

Достоинства реометров этого типа:

• 
  компактность и малый объем жидкости, необходимый для измерений;
  
• 
  возможность создания в зазоре постоянной скорости сдвига;
  
• 
  легкость контроля за температурой и ее регулирование;
  
• 
  хорошая воспроизводимость экспериментальных данных.
  

Недостатки:

• 
  непригодность их для исследования грубых суспензий, если зазоры малы;
  
• 
  возникает погрешность в результатах из-за осаждении твердой фазы в процессе измерений;
  

• 
  варьирование угла закручивания может происходить вследствие изменения концентрации в радиальном направлении под действием центробежных сил.
  
• 
  главным недостатком отечественных реометров является ограниченность и предопределенность скоростей вращения внешнего цилиндра, что ограничивает число опытных точек.
  

23. Расчет перепада давления в промывочных отверстиях долота.

Промывочный узел любого шарошечного долота состоит из участка, где поток ускоряет свое движение (плавное или резкое сужение) и участка свободного истечения (струйного) течения. Таким образом, происходит превращение потенциальной энергии (перепада давления) в кинетическую энергию потока. Любое превращение энергии, как известно, сопровождается потерями.

Если условно кинетическую энергию струи считать "полезной", то потери энергии будут сосредоточены на участке сужения потока. Тогда перепад давления на долоте можно выразить уравнением: 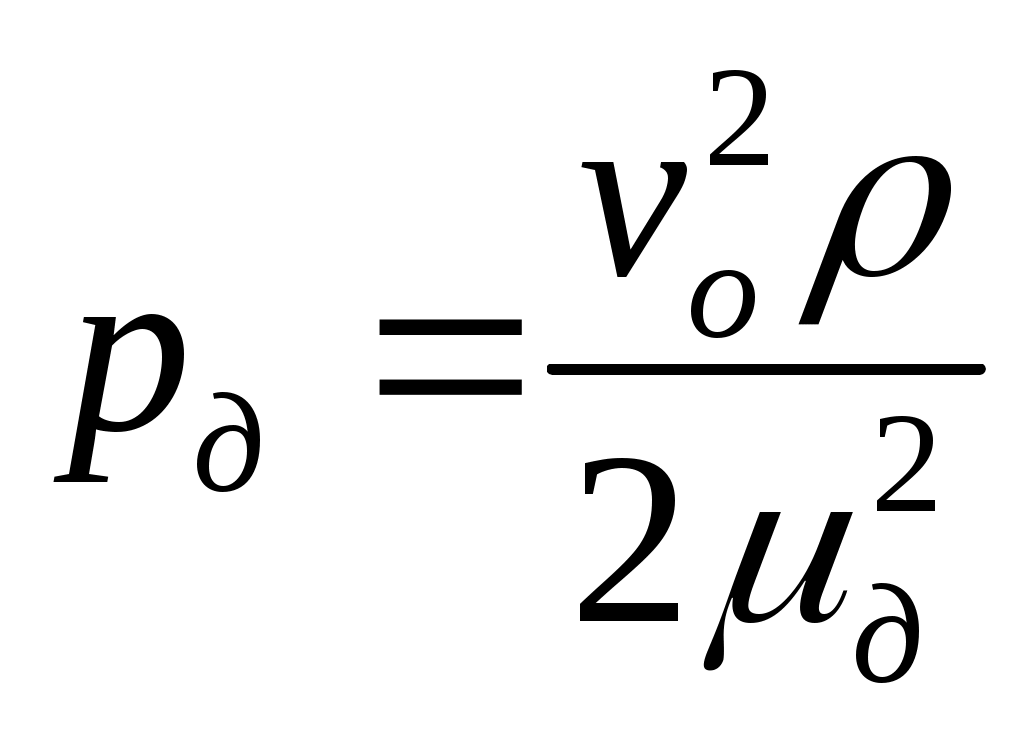, (10.1) где _д - коэффициент местных сопротивлений промывочной системы долота на участке сужения потока; v_o - характерная скорость в одном из сечений местного сопротивления; в данном случае - это скорость в самом узком сечении промывочного канала. Первое слагаемое - это безвозвратные потери давления на "разгон" потока, а второе – "полезная" часть приобретенной энергии, которую буровик надеется с пользой употребить на очистку забоя или долота от шлама. Представим формулу (10.1) несколько иначе. . (10.2) Выражение в скобках принято обозначать соотношением (это мы делали и в разделе 9): , (10.3) где _д - коэффициент расхода промывочного узла долота. Тогда: . (10.4) Если выразить v_o через Q, а суммарное сечение промывочных каналов долота обозначить через f_д , то получим формулу, пригодную для долот любого типа: . (10.5) Для гидромониторных долот, оснащенных одинаковыми по диаметру отверстий d_о насадками в количестве z штук, удобно пользоваться формулой: . (10.6) Коэффициент расхода _д характеризует степень гидродинамического совершенства промывочного узла конкретного долота, величина _д ² - это, по существу, к.п.д. превращения удельной энергии р_д в кинетическую энергию струй v_o²/2 . Поэтому _д всегда меньше 1. Каждое долото, строго говоря, имеет свое конкретное значение _д. Величину _д гидромониторного долота, оснащенного конкретными насадками, можно точно рассчитать. Получению расчетной формулы для определения _д посвящен следующий подраздел.

24. Основные свойства буровых жидкостей.

1.Коллоидность буровых жидкостей, в которых удерживаются во взвешенном состоянии частицы глины, должна составлять 96-98%. Высокая коллоидность бурового раствора делает промывку безопасной. Способность удерживать во взвешенном состоянии частицы разбуренных пород зависит от вязкости раствора.

2. Вязкость раствора с повышением температуры жидкости уменьшается. Она постепенно изменяется в зависимости от скорости течения, степени разрушения структуры, количества твёрдой фазы в ед. объёма. Вязкость нормального глинистого раствора должна быть в пределах 20-25с.

3. Водоотдача раствора. Водоотдача нормального глинистого раствора должна быть в пределах 25-10 см³ за 30 мин.

4. Толщина глинистой корки, отлагаемой на стенках скважины, зависит от водоотдачи раствора и не ложна превышать 3мм.

5. Статическое напряжение сдвига. В нормальных растворах СНС (за 1 мин.) саставляет 1-2 Па и 2-5 за 10 мин.

6. Стабильность глинистого раствора. Для нормальных глинистых растворов стабильность не должна превышать 0,02 г/ см³, для утяжелённых – 0,06 г/ см³.

7. Водородный показатель рН имеет большое значение для суждения о физико-химических процессах, происходящих в глинистом растворе.