шпор тоэ1. 2. Идеалды кернеу кзі (ЭК), идеалды то кзі, баламалы слбалар
 Скачать 322.93 Kb. Скачать 322.93 Kb.
|
    1.Электр тізбегі – бір-бірімен сымдар арқ жалғанатын элементтерден құралған электр және энергияның басқа түрлерінің берілуі, таратылуы және өзара түрленуі үшін арналған құрылғы-ң жиынтығы. Электр тізбегіндегі элементтер-белгілі бір функция атқаратын, электр тізбегіне кіретін құрылғылар. Электр тізб-ң нег элем-не электр энергия көздері және қабылдағыштар жатады. Электр эн-я көздерінде энергияның көптеген түрлері электр эн-на айналады. Ал эл. эн-ң қабылдағыштарында керісінше электр эн-сы эн-ң басқа түрлеріне айналады. Өткізгіштік электр тогы-уақыт бойынша электр зарядынан алынған туынды, қарастырылып отырған бет арқылы өтетін, тасымалдап апаратын зарядқа тең. 1.Электр тізбегі – бір-бірімен сымдар арқ жалғанатын элементтерден құралған электр және энергияның басқа түрлерінің берілуі, таратылуы және өзара түрленуі үшін арналған құрылғы-ң жиынтығы. Электр тізбегіндегі элементтер-белгілі бір функция атқаратын, электр тізбегіне кіретін құрылғылар. Электр тізб-ң нег элем-не электр энергия көздері және қабылдағыштар жатады. Электр эн-я көздерінде энергияның көптеген түрлері электр эн-на айналады. Ал эл. эн-ң қабылдағыштарында керісінше электр эн-сы эн-ң басқа түрлеріне айналады. Өткізгіштік электр тогы-уақыт бойынша электр зарядынан алынған туынды, қарастырылып отырған бет арқылы өтетін, тасымалдап апаратын зарядқа тең. 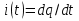 Кернеу-электр өрісі кернеулігінің сызықты интегралы Кернеу-электр өрісі кернеулігінің сызықты интегралы 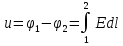 Кернеу мен ток бағыты бірдей. ЭҚК Е-бөгде өрістің жіне индукцияланған электр өрісінің электр тогын қоздыру қабілетін сипаттайды. Қабылдағыш кедергісі R-электр эн тұтынуды, эл эн басқа энергия түріне өзгеруін сипаттайды. Қабылдағыш кедергісі токка тәуелді, кернеуі Ом заңымен анықталады: Кернеу мен ток бағыты бірдей. ЭҚК Е-бөгде өрістің жіне индукцияланған электр өрісінің электр тогын қоздыру қабілетін сипаттайды. Қабылдағыш кедергісі R-электр эн тұтынуды, эл эн басқа энергия түріне өзгеруін сипаттайды. Қабылдағыш кедергісі токка тәуелді, кернеуі Ом заңымен анықталады: 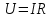 Өткізгіштік-кедергіге кері шама Өткізгіштік-кедергіге кері шама 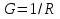 Индуктивтік L-электр тізбегінің идеалды элменті, онда магнит өрісінің эн жинақталады. Конденсатор сыйымдалығы С-конденсатор электродтары арасындағы эл сыйымдылығы,электр өрісінің энергиясы жинақталып, сақталады Индуктивтік L-электр тізбегінің идеалды элменті, онда магнит өрісінің эн жинақталады. Конденсатор сыйымдалығы С-конденсатор электродтары арасындағы эл сыйымдылығы,электр өрісінің энергиясы жинақталып, сақталадыЭлектр сүлбесі – электр тізбектің графикалық көрінісі. Ол электр тізбектің элем-ң қосылуы қалай орындалғанды көрсетеді де, тізбекті есептеде қолданады. Сұлбаның 2 нег элем-рі бар: ЭҚК Е және ішкі кедергісі R көз және қабылдағыштармен сымдардың кедергісі R. ЭҚК-тің әрекет бағытын сұлбада тілмен көрсетеді. Қабылдағыштың кедергісі электр сүлбенің элементі ретінде эн-ң тұтынуын 2. Идеалды кернеу көзі (ЭҚК), идеалды тоқ көзі, баламалы сұлбалар. Кернеу көзіне жататн энергия көзі, шығу қысқышындағы кернеудің сыртқы тізбек қасиеттеріне тәуелді болмайды. Сыртқы қысқыштарындағы кернеу энергия көзінен берілген кернеуі немесе оның жай кернеуі деп аталады. Кернеу көзі шарт бойынша график түрінде келесі түрде белгіленеді. Идеалды ток көзі тоғы жалғанған жүктеме кедергісіне тәуелді емес, ал оның ЭҚК Е және ішкі кедергісі R шексіздікке тең. Екі шексіз үлкен шамалардың қатынасы Е/R шекті шамаға тең. Энергия көзінің балама сұлбаларының түрі. Е/R=I+ U/R=I+ gU немесе J=I+Iішкі J=E/Rішкі . Баламалы сұлбаларға баламалы кедергілердің сұлбалары жатады: параллель, тізбектей, аралас жалғануы. 3. ЭҚК бар тізбек бөлігі үшін Ом заңы. 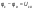 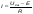 ЭҚК ток бағытымен бағыттас болса, оң таңбамен ал қарама-қарсы болса, теріс таңбамен алынады. Қуаттар балансы: Кез келген тармақталған электр тізбектерінде қорек көздерінің қуаты тұтынушылардың қуатына тең болуы керек. ЭҚК ток бағытымен бағыттас болса, оң таңбамен ал қарама-қарсы болса, теріс таңбамен алынады. Қуаттар балансы: Кез келген тармақталған электр тізбектерінде қорек көздерінің қуаты тұтынушылардың қуатына тең болуы керек. 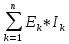 = =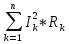 . Sқор.=Sтұт. . Sқор.=Sтұт.4. Тармақталмаған тұрақты тоқ тізбектің потенциалдық диаграммасы. Абцисса бірлігінде таңдалған кедергінің масштабында тізбекке қосылған бөліктерінің кедергілерін, ал ордината бірлігінде сәйкесті нүктелердің потециалдарын салсақ, онда тармақталмаған тізбектің потенциалдық диаграммасы шығады. Мысалы:а нүктенің потенциалы 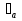 =0 деп алғанда в нүктенің потенциалы: =0 деп алғанда в нүктенің потенциалы:  = = -IR1. Басқа нүктелердің де потенциалы сәйкесінше болады. Тоқ пен кернеудің бағыттарын Ом заңы бойынша аламыз. Әр нүктедегі потенциалдарды анықтау үшін, қарастырылып отырған тізбектің бір нүктесіндегі потенциалын 0-ге тең деп аламыз. -IR1. Басқа нүктелердің де потенциалы сәйкесінше болады. Тоқ пен кернеудің бағыттарын Ом заңы бойынша аламыз. Әр нүктедегі потенциалдарды анықтау үшін, қарастырылып отырған тізбектің бір нүктесіндегі потенциалын 0-ге тең деп аламыз. 5. Тармақталмаған тұрақты тоқ тізбегі. Тармақ, түйін, контур. Тоқтары мен кернеулері уақыт бойынша өзгермейтін тізбектерді тұрақты тоқ тізбектер дейміз. Тізбектеліп қосылған ЭҚК-тердің көздерінен және кедергілерден құралған электр тізбегінің бөлігі тармақ деп аталады. Түйін үш және одан да көп тармақтардың қосылған орны немесе нүктесі электр тізбегінің түйіні деп аталады. Бірнеше тармақтардан өтетін тұйықталған жол электр тізбегінің контуры деп аталады. 6.Тұрақты ток тізбегін контурлық тоқтар әдісімен есептеу. Контурлық токтар әдісі. Контурлық ток-алынған контурдың әр бөлігі үшін бірдей болатын есептеу шамасы. Есептеуді мына ретпен жүргізеді:а)тізбектің барлық тәуелсіз контурындағы контурлық токтардың бағытын бірдей етіп алады(сағат тілі бойынша немесе керісінше);б) контурдың айналу бағытын да сондай бағытпен белгілейді.Кирхгофтың екінші заңы бойынша контурдың әрқайсысына тәуелсіз теңдеулер құрылады. Бұл үшін әрбір контурда кездесетін бөліктердегі ЭҚК-імен контурлық токтардың теңдеу құрылып жатқан контурға қатыстығын қарастырады;в)алынған теңдеулер жүйесін шешіп, контурлық токтарды табады, ол арқылытармақтардағы негізгі токтарды есептейді. Контурлық токтар жәнеолардыайналым бағыттары сағат тілінің бағытымен алынған. 1231контуры үшін: 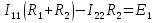 1361контур үшін: 1361контур үшін: 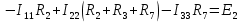 3463контур үшін: 3463контур үшін: 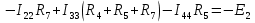 4564контур үшін: 4564контур үшін: 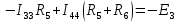 Тармақтардағы негізгі токтарды табу үшін мынаны ескеру керек, егер кез-келген тармақтан тек бір ғана контурлық ток өтсе, негізгі ток контурлық токтың өзіне тең, ал тармақтан бірнеше контурлық ток өтсе, онда негізгі ток осы контурлық токтардың алгебралық қосындысына тең. Тармақтардағы негізгі токтарды табу үшін мынаны ескеру керек, егер кез-келген тармақтан тек бір ғана контурлық ток өтсе, негізгі ток контурлық токтың өзіне тең, ал тармақтан бірнеше контурлық ток өтсе, онда негізгі ток осы контурлық токтардың алгебралық қосындысына тең. 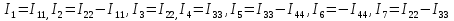 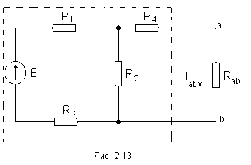 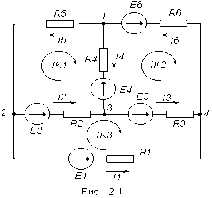 7.Түйіндік потенциалдар әдісімен токтарды анықтау. Кирхгофтың 1 заңына нергіжделген шартты түрде 1 түйіннің потенциалын 0-ге теңестіреміз. Сонда қалған отенциалдар үшін теңдеулер жүйесі келесі түрді қабылдайды. Негізгі потнециал «+» қалғаны «-» (Сурет лекцияда берілген) 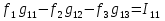 - -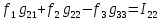 - -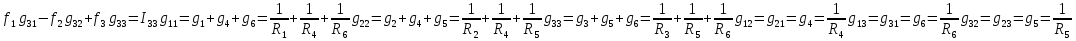 Түйінен шықса «-» кірсе «+» Түйінен шықса «-» кірсе «+»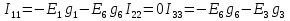 Кез келген әдіспен белгісіз Кез келген әдіспен белгісіз 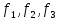 потециалдарын анықтаймыз. Сонда тармақтағы токтар Ом заңы бойынша анықталады. потециалдарын анықтаймыз. Сонда тармақтағы токтар Ом заңы бойынша анықталады.8.Тұрақты ток электр тізбегін екі түйін әдісімен есептеу.Көп жағдайда екі түйіннен тұратын сұлбалар кездеседі. Мұндай сұлбаларда түйіндік әлеуеттер әдісінің жеке түрі екі түйін әдісімен есептеледі. Электр тізбегін есептеу үшін екі қолдану дегеніміз-ол екі түйін арасындағы кернеуді табу.Бұл екі түйін арасындағы 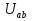 кернеуді табайық: кернеуді табайық: 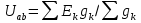 . . 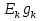 таңбалары жоғарыдағы түйіндік әлеуеттер әдісіндегідей қабылданады. Кернеу табылғаннан кейін, барлық тармақтардағы токты анықтаймыз: таңбалары жоғарыдағы түйіндік әлеуеттер әдісіндегідей қабылданады. Кернеу табылғаннан кейін, барлық тармақтардағы токты анықтаймыз: 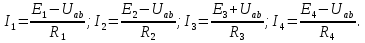 9.Эквивалент генератор әдісі. Кез-келген активті екі полюсті ЭҚК көзінің ж/е кірістік кедергінің тізбектей жалғасуымен көрсетіле алады. Бұл ЭҚК-нің мәні активті екі полюстік қысқыштарына қатысты есептелетін бос жүріс кернеуіне тең болады. Кірістік кедергі активті екі полюстіктен ЭҚК-ді алып тастау жолымен алынған пассивті екі полюстіктің эквиваленттік кедергісіне тең болады. 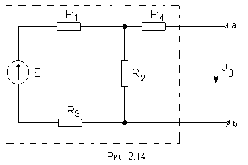 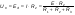 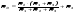 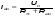 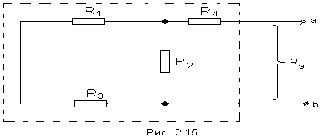 10.Беттестіру әдісі бойынша токтарды есептеуКТӘ-бойынша тендеу жүйесіндегі(*)Е11,Е22,Е33, белгілі бір контурдағы барлық тармақтарының электр қозғаушы күштерінің алгебралық суммасы болып табылыды. Егер осы тендеулерде барлық контурлық электр қозғаушы күштердің, тармақ- тардың электр күштерінің алгебралық қосындысы ретінде көрсетсек,онда контурлық токтар әртармақтын электр қозғауыш күшінің әрекет етуінен пайда болатын,токтардың алгебралық қосындысы ретінде көрсетуге болады.Электр тізбегінің мұндай манызды қйасиеті беттестіру принцпі д.а. Мысал 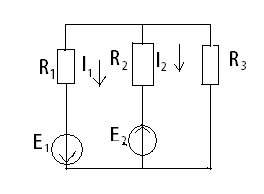 U’12= U’12= (E2 =0) ; I’2 = (E2 =0) ; I’2 = ; ;  = = (E1=0) ; (E1=0) ;   = = ; ;  = = 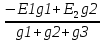 ; ; 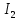 = =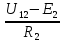 Яғни қандай да бір тармақтың тогын беттестіру әдісімен анықтау үшінсулбадагы электр қозғаушы күштерді кезек-кезек қалдырып қалған ЕҚК-терді 0-ге тенестіріп анықтаймыз,нәтижелері ток сол ЕҚК-нің кезек-кезек әрекет еткен кездегі токтардың алгебралық қосындысна тең болады. 11.Сызықты электр сұлбаларындағы эквиваленттік түрлендірулер. 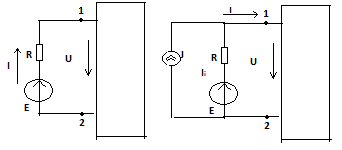 1,18а – суретте ЭҚК-тің көзінен ток көзіне ауысу сұлбалары 1,18а – суретте ЭҚК-тің көзі R ішкі кедергісімен 1 және 2 қысқыштарға жалғанған , ал қысқыштар арасындағы кернеу U. Ток I тең 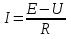 = =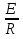 - - 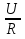 =J-Ii (1,42) =J-Ii (1,42)J= 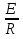 - ток көзінің тогы Ii= - ток көзінің тогы Ii= 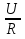 - ішкі кедергідегі токІ- ЭҚК-тің көзінің тогы(1.42) тендеуге 1.18,б – суреттегі эквивалентті сүлбе сәйкес келеді.Токкөзі тогы ЭҚК-тің бағытымен бір бағыттас. - ішкі кедергідегі токІ- ЭҚК-тің көзінің тогы(1.42) тендеуге 1.18,б – суреттегі эквивалентті сүлбе сәйкес келеді.Токкөзі тогы ЭҚК-тің бағытымен бір бағыттас.E (кернеу) көзі идеалды ток көзі Rішк=0 Айқын ток көзі, Rішкі кедергі мен ток көзімен параллель жалғанған эквивалентті схемамен ғана ауыстырылады. 12 Электр тізбектерінің өзаралық қасиетіСызықты электр тізбектерінде қандай да бір m тармағындағы Em ЭҚК әрекет еткендегі к тармағындағы Ek ЭҚК әрекет еткендегі m тармағындағы токқа тең болады. Бұл кезде Ek=Em болуы керек.сонымен қатар ЭҚК ж/е токтардың бағыты бір біріне қатысты бірдей болуы керек.    14. Электр тізбегі тармақтарының кірістік және өзара өткізгіштіктері.Электр тізбегінің кез-келген тармағының кірістік өткізгіштігі сол тармақтағы токтың ЭҚК-іне қатынасымен анықталады. Кірістік өткізгіштіктің индекстері бірдей болады.(бұл кезде қалған ЭҚК-р 0-ге тең болуы керек.)  = = -кірістік өткігіштік Электр тізбектерінің кез-келген 2 тармағының өзара өткізгіштігі бір тармақтағы токтың екінші тармақтағы ЭҚК-іне қатынасымен анықталады. Қалған тармақтағы ЭҚК-р бұл кезде 0-ге тең болуы керек. -кірістік өткігіштік Электр тізбектерінің кез-келген 2 тармағының өзара өткізгіштігі бір тармақтағы токтың екінші тармақтағы ЭҚК-іне қатынасымен анықталады. Қалған тармақтағы ЭҚК-р бұл кезде 0-ге тең болуы керек.  -өзара өткізгіштік. -өзара өткізгіштік.  = = 15. Активті екіұштық теоремасы.Теореманың математикалық өрнегі.Кез-келген активті екі полюсті ЭҚК көзінің ж/е кірістік кедергінің тізбектей жалғасуымен көрсетіле алады. Бұл ЭҚК-нің мәні активті екі полюстік қысқыштарына қатысты есептелетін бос жүріс кернеуіне тең болады. Кірістік кедергі активті екі полюстіктен ЭҚК-ді алып тастау жолымен алынған пассивті екі полюстіктің эквиваленттік кедергісіне тең болады.  16 Компенсация теоремасы Теңгеру теоремасын түсіндіру үшін а,б,в сұлбалар келтірілген. Кез келген кедергіні ЭҚК көзіне ауыстыруға болады. Оның бағыты ток бағытына қарама қарсы және сол кедергідегі кернеуіне тең. Бұл теңгеру теоремасы. Дәлелдеу үшін б суретінде д нүктесінен с нүктесіне өткенде әуелет(потенциалдар) E11=U1 шамасына көбейеді. Ал с нүктесінен в нүктесіне өткенде сол шамаға азаяды, осының салдарынан әлеует бір бірәне тең.сондықтан осы нүктелерді өткізгішпен тұйықтап қосуға болады,яғни ЭҚК көзі және кедергісі сұлбадан алып тасталынған бұдан басқа барлық тармақтағы ток өзгермейді.  17.Синусоидалы ток тізбектері.Синусоидалы шамалар. Синусоидалы - деп sin заңы б/ша өзгеретін ж/е уақыт б/ша өзгер-н токты айт-з. Синусоидалық токтың лездік мәні мына өрнек-н анық-ды:i=Imsin(2πt/T+ψ)= Imsin(ωt+ψ), мұнд Im –ток амплитудасы, яғни токтың ең үлкен мәні; синус аргументі 2πt/T+ψ–фаза д.а. Бұрыш ψ-бастапқы уақыт мезгіліндегі (t=0) фазасына тең, сонд-н оны бастапқы фаза д.а.Синусоидалы ток тізб-ң элемент-і:1.активті кедергі R;Бұл токтың лездік кернеуі u=Umsinωt.Ом заңы б/ша u=iR=ImRsin ωt; Тұж-а: активті кедергіде ток пен кернеу фаза б/ша сәйкес келеді.активті кедергіге келіп түсетін қуат келесі өрнекпен анықт-ы: P=ui=UmsinωtImsinωt=UIsin2ωt=UmIm(1-cos2ωt)/2. Син-ы ток тізб-і индуктивтілік: ХL=ωL=2πfL; UL=LdI/dt кернеу-ң лездік мәні. Индуктивтіліктегі кернеу векторы ток векторынан 90̊ озып отырады. Сыйымдылық кедергі: Хс=1/ωС; u=1/c 0ʃπίdt. Сыйымд-қ кедергіде ток векторы кернеу вект-н 90̊-қа озады. Синусоидалыэлектршамалар – электр тізбекте кернеудің және токтын лездік шамалары тең уакыт аралык саиын каиталанатын процесс периоды деп аталады.Периодты шаманын мәні кайталанатын ен аз уакыты период деп аталады.Синусоидалы шаманын озгеріп тұрган мәнін белгілейтін шама  фаза депаталады .Уакытагымыбойынша фаза оседі. 2πшамага фаза оскенненкеинсинусойдалышаманынозгеру циклі каиталанады фаза депаталады .Уакытагымыбойынша фаза оседі. 2πшамага фаза оскенненкеинсинусойдалышаманынозгеру циклі каиталанады 18. Aктивті кедергідегі синусоидалы тоқ. Активті кедергідегі тоқ, кернеу, қуат(лездік және кешенді түрлері). Лездік мәндер графигі. Векторлық диаграммасы.  19.Индуктивтіктегі синусоидалы тоқ.   Кернеудің лездік мәні Кернеудің лездік мәні  (индуктивтілік кешенді кедергі) (индуктивтілік кешенді кедергі) 20.Сыйымдылықтағы синусоидалы тоқ.  Егер де С сыйымды лықтағы кернеу синусойдалы болса,  онда тоқ: онда тоқ:  көрініс көрініс көрсетіп тұр: тоқ  ынта салынған кернеуден ынта салынған кернеуден  бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.Фазалық ығысу: бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.Фазалық ығысу:    –сыйымдылық кедергі, ал оған кері шама bC= –сыйымдылық кедергі, ал оған кері шама bC= – сыйымдылық өткізгіштік деп аталады. Сонымен, – сыйымдылық өткізгіштік деп аталады. Сонымен,  Сыйымдылықтағы лезді қуат:  Бұл қуат амплитудасы UI, ал бұрыштық жиілігі 2  тең синусойдалы заң бойынша тербеленеді, яғни көрініс тең синусойдалы заң бойынша тербеленеді, яғни көрініс  сияқты. Сыйымдылықтың электр өрісінің энергиясы: сияқты. Сыйымдылықтың электр өрісінің энергиясы: 0-ден  – ге дейін шектерде бұрыштық жиілігі – ге дейін шектерде бұрыштық жиілігі  -мен периодикалы өзгеріп тұрады. -мен периодикалы өзгеріп тұрады.Көзбен сыйымдылықтың арасында энергияның тербеленуі өтеді, ал сыйымдылыққа түсетін активтік қуат нөлге тең. Сыйымдылық кедергіні былай табуға болады:  21.Синусойдалы шамалардын лездик жане комплекс турлери: Лездиктури:  , ,  , ,  Комплекс тури:  , ,  , ,  Кернеу мен Токтын арекет мани:  , ,   , ,  , ,  , ,  Орташа мандери:  , ,  , ,  22. R,L,C элементтерініің тізбектей жалғануы. Векторлық диаграммасы.  ; ;  u=uR+uL+uC u=i*R+L*di/dt+1/cʃidt U=I*R+I*jXL+I*(-jXc)= I(R+j(Xl-Xc)); 23.R,L,C элементтерінің паралелль жалғануы.Векторлық диаграмма. Егер де R,L,С элементтер параллельді қосылған тізбекке синусойдалды кернеу  ) ынта салынса, онда бұл тізбектен өткен ток параллельді тармақтардан өтетін токтардың алгебралық қосындысына тең (Кирхофтың I заңы б\ша): ) ынта салынса, онда бұл тізбектен өткен ток параллельді тармақтардан өтетін токтардың алгебралық қосындысына тең (Кирхофтың I заңы б\ша):  ;I=Ir+Il+Ic;U=Ur+Ul+Uc;u=u*e(jᵠ) ;I=Ir+Il+Ic;U=Ur+Ul+Uc;u=u*e(jᵠ)Ом заңы бойынша тармактагы токтар Ir=  : :Индуктивті ток: Il=  Сыйымд. Ic=  = = R кедергідегі  ток U кернеумен фаза бойынша біртектес, L индуктивтігі ток U кернеумен фаза бойынша біртектес, L индуктивтігі  ток ток  бұрышқа қалады, ал С cыйымдылықтағы бұрышқа қалады, ал С cыйымдылықтағы  ток π/2 бұрышқа u кернеуден озады. ток π/2 бұрышқа u кернеуден озады.24.Синусоидалы ток тізбектеріндегі қуаттары. Тізбектің кернеуі u=UmSINwt,ал тогы i=ImSIN(wt-u). Лезді қуат: P=ui=UmImsinwtsin(wt-u)=UI[cosu-cos(2wt-u] Яғни екі бөліктен құралады:тұрақты шама UIcosu және кернеумен токтын жиіліктерінен екі есе үлкен сонусоидалы шамадан T уақыт ішінде екінші қосындының орташа мәні нөлге теңСондықтан тізбектегі активтік қуат P=  =UTcosu =UTcosuCosu-қуат коэфициент д.a Активтік қуат баска турде көрсетуге болады P=R  =g =g = = =U =U Кедергі және индуктивтігі бар тізбекті карап шыгайыкБұл жаіғдайда 0 u және i таңбалары бірдей кездегі уакыт аралыкта лезді куат болымды;энергия көзден қабылдағыш қа түседі де кедергіге жұтылады және индуктивтің магнит өрісінде қолданады. u және i таңбалары кері кездегі уакыт аралыкта лезді куат теріс; энергияның бір бөлігі көзге қайтадыАктивтік сыйымдылық тізбекте көрініс ұқсас болады(0>u>-  ). Активті қуат.Активті қуат деп лездік қуаттың бір периодтағы орташа мағынасы: ). Активті қуат.Активті қуат деп лездік қуаттың бір периодтағы орташа мағынасы:  . Синусоидалы ток үшін активті қуат: . Синусоидалы ток үшін активті қуат:  тең. Мұндағы U,I – қолданылған кернеу мен токтың мәні, тең. Мұндағы U,I – қолданылған кернеу мен токтың мәні, -кернеу мен токтың фазалар айырымы.Активті қуаттың өлшем бірлігі-Ватт (Вт). -кернеу мен токтың фазалар айырымы.Активті қуаттың өлшем бірлігі-Ватт (Вт).Реактивті қуат. Реактивті қуат тепе-теңдігі:  .Мұндағы x,b –реактивті кедергі мен өткішгіштік.Өлшем бірлігі-ВАр түрінде жазылады. .Мұндағы x,b –реактивті кедергі мен өткішгіштік.Өлшем бірлігі-ВАр түрінде жазылады.Толық қуат.Толық қуат теңдеуі:S=UI.Өлшем бірлігін-ВА(вольт-ампер).Синусоидалы ток үшін активті,реактивті және толық қуат былай байланыстырылады:  . .Кешенді қуат.Кешенді қуат теңдеуі:  .Мұндағы .Мұндағы  мына токпен түйістірілген токтың кешені. мына токпен түйістірілген токтың кешені. 26.Топографиялық сызба - бұл кешенді потенциялдар сызбасы. Сұлбаның әрбір нүктесі топографиялық сызбаның нүктелеріне сәйкес келеді. Потенциялы 0-ге тен нүкте, топографиялық сызбаның бас кординатасына сәйкес келеді. Топографиялық сызба қолдану арқылы нүктелер арасындағы кернеуді азайтуға болады. Топографиялық сызбадағы кернеу векторы нүктеге қатысты сәйкесінше нүктелерге оң бағытталған кернеуге қарама-қарсы бағытталған. Топографиялық сызбаны тұрғызу үшін нүктелердің кешенді потенциялдарын анықтап алып, анықталған мәндерді кешенді жазықтықта тұрғызамыз.Топографиялық сызбаны салуға мысал келтірілген:  28.Комплексті кедергілердің параллель жалғанған кездегі тізбекті есептеу: Екі параллелді тармақтары бар: біреуі кедергімен және индуктивтілікпен, екіншісі кедергімен және сыйымдылықпен тізбекті қосылған сұлбаны қарап шығайық. Мұндай тізбекті параллель тербелмелі контур деп атайды. Яғни Z1,Z2 кедерг3лер3 параллель жалғанған. Бұл кезде әрбір кедергінің кернеулері кіріс кернеуіне тең болады U=U1+U2, ал ток күші әрбір ток күштерінің қосындысы кірістегі токка тең болады. Толық ток күші I=U/Z; I1=U1/Z1; Z1= R1+jXL1; Z2=R2+jXC2; I2=U2/Z2; I=I1+I2; Z=Z1*Z2/(Z1+Z2); Векторлық диаграммада кескіндейтін болсақ кірістегі ток әрбір елементтердің токтарының қосындысына тең болып шығуы қажет. 29.Комплексті кедергілердің аралас жалғанған кездегі тізбекті есептеу: Аралас жалғану ол бірізді және паралель жалғанған кедергілердін тіркестері: Комплексті кедергілері z1,z2,z3 сәйкесінше аралас жалғанған. Жалпы кедергі z=z1+  .Сонда тоқ күштерін есептейміз I1=U/z; I2=I1*z3/(z2+z3); I3=I1*z2(z2+z3); Векторлық диаграммада I1=I2+I3 болып шығуы керек. .Сонда тоқ күштерін есептейміз I1=U/z; I2=I1*z3/(z2+z3); I3=I1*z2(z2+z3); Векторлық диаграммада I1=I2+I3 болып шығуы керек.Кернеулері  U2=I2*Z2; U3=I3*Z3; Барлық тармақтардағы кернеулердін қосындысы кірістегі кернеудін шамасына тен болады. Векторлық диаграммада U1=U2+U3 болып шығуы керек. Векторлық диаграммада токтардың бағыты сәйкесінше кернеуледің бағытымен бағыттас болып шығуы тиіс. Диаграмманы өзің сызып ал. U2=I2*Z2; U3=I3*Z3; Барлық тармақтардағы кернеулердін қосындысы кірістегі кернеудін шамасына тен болады. Векторлық диаграммада U1=U2+U3 болып шығуы керек. Векторлық диаграммада токтардың бағыты сәйкесінше кернеуледің бағытымен бағыттас болып шығуы тиіс. Диаграмманы өзің сызып ал.30.Тармақталған синусоидалы ток тізбектері үшін Кирхгоф заңдары. Дифференциалдық түр- дегі Кирхгофтың заңдары айнымалы токтар мен кернеулердің лездік мәнін жазуға көмектеседі. Кирхгофтың 1 заңы: сұлбадағы токтың лездік мәндерінің қосындысы нольге тең бт:  =0 =0Кирхгофтың 2 заңы: ЭҚКнің лездік мәнінің барлық тұйықталған контурдағы кернеудің алгебралық қосындысы, сол контурдағы элементтердің кернеулерінің алгебралық қосындысына тең:  Кешенді түрдегі Кирхгофтың заңдары кешенді амплитуда және токтың, кернеудің, ЭҚКнің кешенді мәндері үшін жазылады Кирхгофтың 1 заңы: сұлбадағы түйіндердің комплекстік токтың мәндерінің алгебралық қосындысы нөлге тең болып табылады:  =0 I с точкой напиши и на индекс к впиши. =0 I с точкой напиши и на индекс к впиши.Кирхгофтың 2 заңы: кешенді ЭҚКнің барлық тұйықталған контурдағы кернеудің алгебралық қосындысы, сол котурдағы элементтердің кернеулерінің алгебралық қосындысына тең:  (RkIk+LKIKjw - (RkIk+LKIKjw - Кирхгофтың заңдарын кешенді түрде анықтайтын теңдеулер Синусоидалды ток үшін:  =0 =0  = = Сол сияқты тұрақты ток үшін:  =0 =0  = = 31. Контурлық тоқтар әдісімен синусоидалы ток тізбектерін есептеу. Берілген тізбекте контурлардың бойымен өтетін кешендік контурлық тоқтарды енгіземіз . олардың бағытын өз еркімізбен таңдаймыз . сол КТ қатысты теңдеу жүйесін құрып , белгісіз кешенді токтарды анықтаймыз.  ( ( + + - - + + + + )- )- ( ( + + )= )= -  ( ( + + )+ )+ ( ( + + + + - - )= )=  = = + + - -  = = + +  = = - -  ( ( + + )- )- = = -  + + ( ( + + )= )= Сонда тармақтағы кешенді тоқтар келесі түрде анықталады  = = = = - - = = 32.ТПӘ мен синусоидалы тоқ тізбек-н есеп-у. Бұл әдіс Кирх 1-заңына ж/е Омның з-н қолд-ға нег-н.Күрделі тізбек-ң қайсысы болған түйін-ң потенц-н нһлгетең деп алуға б-ы.Басқа түйіндермен базистік түйін-ң ара-ғы кернеу сол түйіндер-ң потенциалы б-ы.Бұл потенц-ды тармақ-ң өткізгіш-не көбейткенде сол тармақтағы ток табыл-ы.Егерде электр тізбек-гі түйінді потенц-рды тапсақ,онда тармақ-ң ток-н таб-з. К 1-заңы б/ша 1 ж/е 2 түйін-р үшін  Y11  -Y21  Y=1/z; Y11=Y1+Y3+Y4;Y12=Y21=Y3;Y13=Y4;Y23=Y5;Y22=Y2+Y3+Y5; 33.Екі түйін әдісі ТПӘ-нің жеке жағдайы болып табылады. Яғни бұндай тізбекте тек 2 түйін болуы керек. Түйіндер арасындағы кернеу комплексін есептейміз:  Мұндағы,  , ,  Тармақтардағы тоқтар комплекстерін Ом заңы бойынша есептейміз:  40 Өзара индуктивті байланысқан элементтердің параллель жалғануы          41.Синусоидалы ток тізбектері үшін қуаттар тепе-теңдігі. Энергияның сақталу заңынан шығатыны-ол кез келген тізбекте лездік және активті қуаттарының да тепе-теңдіктері сақталады.Энергия көздерінен беріліп тұрған барлық қуаттарының қосындысы,барлық қабылдағыштардағы қабылданған қуаттардың қосындысына тең.Комплекстік үшін де тепе-теңдіктің сақталатынын көрсетеді. Сұлбаның жалпы түйіндер саны n болсын делік.Мұндағы түйін дегеніміз-ол сұлбаның кез-келген екі немесе одан да көп элементтерінің қосылған жері.Тармақ дегеніміз-сұлба элементтерінің біреуінен тұратын әрбір сұлба телімі. Әрбір n түйін үшін Кирхгофтың бірінші заңы бойынша комплекстер үшін оған түйіндес жиынтық токтарға теңдеулер құрамыз:  36.КЕРНЕУ РЕЗОНАНСЫ, РЕЗОНАНСТЫҚ ТӘУЕЛДІЛІКТЕР Айнымалытоктізбегініңтолықкедергісі , ал конденсатордағыкернеу мен катушкадағыкернеуамплитудаларыбір-бірінетеңжәнефазаларықарама-қарсы. Ом заңыбойынша ток амплитудасы  37.Ток резанансы. жиілік мейлі дірілдегіш нобай мен a меншікті тербеліс жиілік бар, және мейлі ол к f айнымалы қырман генератор подключен осындай. В кез қосудың электржинағыш бастаудан деген оқталады. Кейін ненің ол орауышқа деген сейілу бастайды, причем осындай жылдамдықпен сейіледі, қандаймен кернеу генераторда кемійді. Аздан кейін электржинағыштің қайраты толықтай орауыштың магниттік даласының қайратына деген ауысады. Кернеу генератордың клеммаларында в осы кезді нөлге тең. Бұдан әрі орауыштың магниттік даласы кеміу бастайды, себебі стационар- лық - орауыштың тұжырымдарында эдс индукциялер өмір сүру білмейді біт-, нешінші электржинағышті перезаряжать бастайды. Дірілдегіш нобайдың қатарында қырман ағады, ғана уже кереғар зарядтың қырманының, себебі айланыстар даламен арада қарама-қарсы бағытта пересекаются. Электржинағыштің айнала қоршаулары кереғар алғашқы зарядтармен перезаряжаются. Мезгілдес кернеу генераторда өседі, причем баяғы жылдамдықпен, қандаймен орауыш электржинағышті оқтайды. 39. Өзара индуктивті байланысқан элементтердің тізбектей жалғануы. Үйлесімді екі орауыштың бірізді жалғанған  сұлбасы келтірілген. сұлбасы келтірілген. бір-біріне қарсы қосылған екі орауыштың бірізді жалғанған сұлбасы келтірілген. Бір-біріне қарама-қарсы қосылған орауыштарда ток кез келген уақыт сәтінде осы екі элемент арқылы аттас белгілермен салыстыра қарағанда, бір біріне қарама қарсы бағытта ағады, сондықтан әрбір элементпен ілескен магнит ағындарының өздік индукциясы бір бірімен алынады. бір-біріне қарсы қосылған екі орауыштың бірізді жалғанған сұлбасы келтірілген. Бір-біріне қарама-қарсы қосылған орауыштарда ток кез келген уақыт сәтінде осы екі элемент арқылы аттас белгілермен салыстыра қарағанда, бір біріне қарама қарсы бағытта ағады, сондықтан әрбір элементпен ілескен магнит ағындарының өздік индукциясы бір бірімен алынады.Екі бірізді жалғанған индуктивті байланысы бар элементтердің индуктивтілігі:  мұндағы мұндағы  және және  бірінші және екінші элементтердегі ағын ілінісуі және де бірінші және екінші элементтердегі ағын ілінісуі және де  оң таңба үйлесімді, ал теріс таңба қарама қарсы қосылғанда орауыштар алынады. Индуктивті байланысқан элементтердің тізбектей жалғануы. үйлесімді екі орауыштың бірізді оң таңба үйлесімді, ал теріс таңба қарама қарсы қосылғанда орауыштар алынады. Индуктивті байланысқан элементтердің тізбектей жалғануы. үйлесімді екі орауыштың бірізді  жалғанған сұлбасы келтірілген. жалғанған сұлбасы келтірілген.   4.6 б-суретте бір-біріне қарсы қосылған екі орауыштың бірізді жалғанған сұлбасы келтірілген. Бір-біріне қарама-қарсы қосылған орауыштарда ток кез келген уақыт сәтінде осы екі элемент арқылы аттас белгілермен салыстыра қарағанда, бір-біріне қарама-қарсы бағытта ағады, сондықтан әрбір элементпен ілескен магнит ағындарының өздік индукциясы бір-бірімен алынады. Екі бірізді жалғанған индуктивті байланысы бар элементтердің индуктивтілігі: L=Ψ/i=Ψ1+Ψ2/i, мұндағы Ψ1 және Ψ2 бірінші және екінші элементтердегі ағын ілінісуі және де Ψ1 =LiΨ2 оң таңба үйлесімді, ал теріс таңба қарама-қарсы қосылғанда орауыштар алынады. 4.8а,б-суреттерде үйлесімді және қарама-қарсы қосылған жағдайларға салынған векторлық диаграммалар. Мұндағы: a)U1=I[Ri+jω(L1+M)]; b) U2=I[R2+jω(L2+M)]. 4.6 б-суретте бір-біріне қарсы қосылған екі орауыштың бірізді жалғанған сұлбасы келтірілген. Бір-біріне қарама-қарсы қосылған орауыштарда ток кез келген уақыт сәтінде осы екі элемент арқылы аттас белгілермен салыстыра қарағанда, бір-біріне қарама-қарсы бағытта ағады, сондықтан әрбір элементпен ілескен магнит ағындарының өздік индукциясы бір-бірімен алынады. Екі бірізді жалғанған индуктивті байланысы бар элементтердің индуктивтілігі: L=Ψ/i=Ψ1+Ψ2/i, мұндағы Ψ1 және Ψ2 бірінші және екінші элементтердегі ағын ілінісуі және де Ψ1 =LiΨ2 оң таңба үйлесімді, ал теріс таңба қарама-қарсы қосылғанда орауыштар алынады. 4.8а,б-суреттерде үйлесімді және қарама-қарсы қосылған жағдайларға салынған векторлық диаграммалар. Мұндағы: a)U1=I[Ri+jω(L1+M)]; b) U2=I[R2+jω(L2+M)].  Тізбектің кіреберістегі жиынтық кедергісі (4.6-сурет): Z=U/I=(U1+U2)/I=Z1+Z2+2ZM; Z1=R1+jωL1, Z2=R2+jωL2, ZM=jωM. 38_Өзара индуктивті байланысқан элементтер, өзіндік және өзара индукция ЭҚКНа рис. показаны две катушки с числом витков W(1) и W(2) магнитный поток первой катушки  пропорционален протекающему по ней току пропорционален протекающему по ней току  . Часть этого потока . Часть этого потока  пронизывает витки второй катушки и оказывает влияние на ток пронизывает витки второй катушки и оказывает влияние на ток  . .Аналогично магнитный поток второй катушки пронизывает витки первой. Такие катушки называются индуктивно – связанными (или магнитно-связанными). Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи k, который определяется отношением:  =<1 =<1где М - взаимная индуктивность элементов цепи, Гн.  - индуктивности элементов, Гн. - индуктивности элементов, Гн.Вообще, взаимной индуктивностью первой и второй катушек называется отношение добавочного потокосцепления второй катушки  к току к току  первой катушки: первой катушки:   Индекс 12 показывает, что взаимная индуктивность наводится в первой катушке от действия магнитного потока второй катушки. Опыт показывает, что:   Взаимная индуктивность в линейных электрических цепях не зависит от направлений и значений токов, и определяется только конструкцией катушек их взаимным расположением. Индуктивность катушки :  При составлении уравнений для магнитно-связанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции. Правильное заключение об этом можно сделать, если известно направление намотки катушек на сердечнике и выбрано положительное направление токов в них.  |
