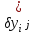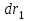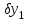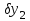Киселев-2. 2. математические модели в технической диагностике Основные понятия
 Скачать 474.94 Kb. Скачать 474.94 Kb.
|
|
2.6 Аналитические модели на основе алгебраических уравнений Если связь между входным возмущением, внутренними параметрами объекта диагностирования и выходными диагностическими параметрами представлена в виде алгебраического уравнения или системы алгебраических уравнений, то мы имеем аналитическую модель алгебраического вида. В зависимости от физического характера объекта диагностирования алгебраические уравнения могут быть линейными или нелинейными. В простейшем случае при описании объекта диагностики подобными моделями задается система линейных алгебраических уравнений, в которых количество уравнений равно числу неизвестных параметров технического состояния или числу диагнозов (то есть числу выбранных для диагноза технических состояний). Рассмотрим случай представления моделей в виде системы линейных алгебраических уравнений. В общем виде 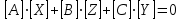 . (2.21) . (2.21) В этом уравнении X , Z, Y соответственно вектор входных возмущений, действующих на объект, вектор внутренних параметров объекта, вектор выходных диагностических параметров. Матрицы А , В , С являются матрицами коэффициентов уравнения. При проведении диагностирования, как правило, располагают значениями диагностических параметров (т.е. известен вектор [Y]), по которым необходимо определить значения входных или внутренних параметров (т.е. определить векторы [X] или [Z]). С точки зрения математического решения задачи диагностики между векторами входных параметров [Х] и вектором внутренних параметров [Z] нет различий. Поэтому векторы [Х] и [Z] можно объединить в общий вектор [R], который называется вектором влияющих факторов, и тогда уравнение (2.21) примет вид 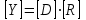 . (2.22) . (2.22) Вектор 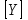 c компонентами yi называют еще вектором отклика системы на вектор возмущающих факторов [R] с компонентами rj. c компонентами yi называют еще вектором отклика системы на вектор возмущающих факторов [R] с компонентами rj. Большинство линейных моделей, приведенных к окончательному виду, разрешены относительно выходных диагностических параметров (откликов) и описываются системой уравнений вида (2.26). Каждое отдельное уравнение в этой системе представляет собой зависимость одного отклика от нескольких влияющих факторов. В большинстве случаев для задач диагностики имеют значение не абсолютные величины параметров, а отклонение этих параметров от нормы. Поэтому, с учетом линейности системы уравнений, заданных выражением (2.22), его предпочтительнее переписать в виде 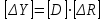 , (2.23) , (2.23)где [Y] - вектор отклонений диагностических параметров (откликов); [R] - вектор отклонений влияющих факторов. Линейность модели позволяет представить отклонения в относительном виде, что является особенно удобным : 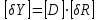 . (2.24) . (2.24) Вектор [Y] есть вектор относительных отклонений откликов (диагностических параметров), который задается своими компонентами yi. Вектор [R] есть вектор относительных отклонений влияющих факторов, который задается своими компонентами rj. Матрица [D] называется матрицей коэффициентов влияния. Каждая строка такой матрицы содержит коэффициенты, которые показывают во сколько раз (на сколько %) изменится данный отклик (выходной диагностический параметр) при изменении одного из возмущающих факторов на 1%. Матрицу [D] удобно представлять в табличном виде. Такая таблица называется таблицей коэффициентов влияния и выглядит следующим образом. В заголовках столбцов указываются относительные отклонения влияющих факторов rj. В заголовках строк указываются относительные отклонения откликов (диагностических параметров) yi. В клетке, лежащей на пересечении i-й строки и j-го столбца, записывается соответствующий коэффициент влияния dij, который показывает на сколько процентов изменится i-й отклик при изменении j-го влияющего фактора. Такая таблица (табл. 2.11) похожа на таблицу состояния, однако в этой таблице размешены не нули или единицы, а коэффициенты влияния. Таблица 2.11 Общий вид таблицы коэффициентов влияния
Использование таблицы коэффициентов влияния уже позволяет решать задачи определения технического состояния. Например, зная изменение откликов, оценить изменение влияющих факторов, которые непосредственно связаны с параметрами технического состояния. Отметим, что на практике диагностические задачи чаще всего формулируются следующим образом: по известным измеренным значениям диагностических параметров (откликов) yi определить техническое состояние (поставить диагноз). Если считать, что влияющий фактор rj определяет какую-либо неисправность, а все отклики (диагностические параметры) могут быть измерены, то предыдущее выражение (2.24) может быть представлено в виде, позволяющем напрямую решать сформулированную выше задачу: [R] = [D]-1[Y] . (2.25) Матрица [D]-1 является обратной для матрицы коэффициентов влияния [D] и называется диагностической [1]. Диагностическую матрицу также можно представить в виде таблицы, где заголовками столбцов являются отклонения измеряемых параметров yi, а заголовками строк - диагнозы технического состояния, определенные отклонениями влияющих факторов rj. Данная таблица также похожа на таблицу состояний и ее можно использовать для решения задач диагностики. Отметим также, что в этом классе моделей могут использоваться алгебраические выражения, в которых несколько откликов связаны с несколькими факторами и они не разрешены относительно откликов, например следующего вида: [C][Y] = [A][R], где [C] и [A] - матрицы коэффициентов влияния соответственно для откликов и для влияющих факторов. Эту систему уравнений можно решать путем последовательной подстановки или в матричном виде: [Y] = [C]-1[A][R]. Сделав подстановку [D] = [C]-1[A], получим выражение, соответствующее формуле (2.24). Таким образом, соответствующими преобразованиями и в этом случае можно получить искомую матрицу коэффициентов влияния или диагностическую матрицу. Мы рассмотрели случай представления модели в виде системы линейных алгебраических уравнений. Однако модель может быть представлена в виде системы нелинейных алгебраических уравнений. Если первоначальные алгебраические уравнения, описывающие объект, представлены в нелинейном виде, необходимо произвести их линеаризацию. Линеаризацию проводят в зависимости от вида нелинейности функции. Ниже рассмотрим несколько наиболее часто встречающихся варианта [1]. 1. Пусть алгебраическое уравнение, связывающее отклик y с факторами rj, имеет вид 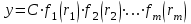 , (2.26) , (2.26)то есть в виде произведения функций. При задании функции в таком виде для линеаризации проводится сначала логарифмирование, а затем дифференцирование исходного выражения. После логарифмирования выражения (2.26) получим следующее уравнение: 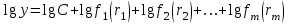 . .После дифференцирования получим соответствующее уравнение: 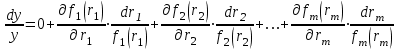 . .Каждый член в правой части уравнения умножим и разделим на абсолютное значение соответствующего влияющего фактора. Например, первый член будет иметь вид 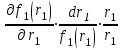 . .Введем следующие обозначения: 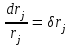 - относительное изменение j-го влияющего фактора; - относительное изменение j-го влияющего фактора; 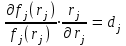 - коэффициент влияния j-го влияющего фактора на относительное изменение диагностического параметра y. Если произвести соответствующую подстановку, то получим окончательное уравнение в следующем виде: - коэффициент влияния j-го влияющего фактора на относительное изменение диагностического параметра y. Если произвести соответствующую подстановку, то получим окончательное уравнение в следующем виде: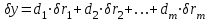 . (2.27) . (2.27) Полученное в результате уравнение является линейным уравнением и связывает между собой относительное изменение измеряемого диагностического параметра (отклика) с относительными изменениями определяющих факторов. 2. Пусть уравнение, связывающее отклик и влияющие факторы, имеет более общий вид: 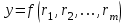 . (2.28) . (2.28)В этом случае логарифмирование нецелесообразно. Уравнение вида (2.28) следует дифференцировать непосредственно: 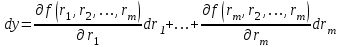 . .Полученное выражение производной далее следует разделить на исходное уравнение, описываемое формулой (2.28): 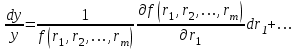 . .Здесь для упрощения записи представлен только первый член правой части. Каждый член правой части, как и в первом случае, умножается и делится на абсолютное значение влияющего фактора. Для примера, первый член правой части будет иметь вид  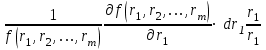 . Введем, как и в предыдущем случае, понятие коэффициента влияния и обозначим его 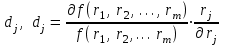 . Тогда, используя понятия относительное изменение влияющего фактора и относительное изменение отклика, после окончательных преобразований получим . Тогда, используя понятия относительное изменение влияющего фактора и относительное изменение отклика, после окончательных преобразований получим 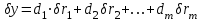 . (2.29) . (2.29)Таким образом, мы вновь получили линейное алгебраическое уравнение, разрешенное относительно отклика. 3.В ряде случаев не удается разрешить уравнение относительно одного отклика. Предположим, что функция имеет вид 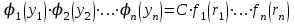 . (2.30) . (2.30)Поскольку уравнение (2.30) представляет собой произведение нескольких сомножителей, то первоначально следует провести логарифмирование этого выражения: 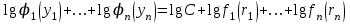 . .Следующим этапом проведем дифференцирование левой и правой частей. Для упрощения записи оставим только первые члены левой и правой частей: 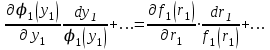 . .Далее, в левой части каждый член умножаем и делим на абсолютное значение соответствующего диагностического параметра, а в правой части каждый член умножаем и делим на абсолютное значение фактора. Введем, как и ранее, понятие коэффициента влияния для каждого влияющего фактора (обозначим dj) и аналогично понятие коэффициента влияния при соответствующих откликах (обозначим bi). Используя эти понятия, окончательное выражение для относительных изменений откликов и относительных изменений влияющих факторов запишем в виде (для упрощения записи оставим только первых два члена левой и правой частей): 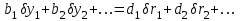 . (2.31) . (2.31)Полученное выражение также определяет линейное алгебраическое уравнение. Наиболее общий случай имеет место тогда, когда и левая, и правая части уравнения описываются алгебраическими уравнениями общего вида: 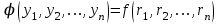 . (2.32) . (2.32)Поскольку выражение (2.32) нельзя представить в виде произведения сомножителей, то логарифмирование не имеет смысла. На первом этапе линеаризации проводится дифференцирование выражения: 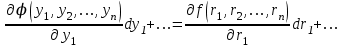 . .Здесь для упрощения записи представлены только первые члены левой и правой частей продифференцированного уравнения. В ходе дальнейших преобразований разделим полученное выражение на исходное. Как и ранее, для упрощения записи представим только первые члены левой и правой частей: 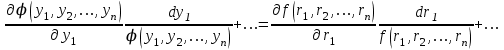 . . . .Если теперь каждый член левой части поделить и умножить на абсолютное значение соответствующего диагностического параметра, а каждый член правой провести соответствующие преобразования, то в окончательном виде получим уравнение, соответствующее выражению (2.31). Приведенные примеры показывают, что если объект диагностики описывается моделью в виде системы алгебраических уравнений, в любой ситуации можно перейти к системе линейных алгебраических уравнений, выраженных относительно каждого параметра или отклика. Путем соответствующих преобразований определить (получить) матрицу (таблицу) коэффициентов влияния или диагностическую матрицу (таблицу). Рассмотрим пример применения диагностических моделей в виде алгебраических уравнений. Наиболее ярким примером использования подобного класса моделей являются модели, которые созданы для диагностирования проточной части авиационных газотурбинных двигателей (ГТД) и их систем регулирования по термогазодинамическим параметрам [1, 10, 30, 31, 42]. Для построения диагностических моделей авиационных ГТД при решении задач диагностирования ГВТ и систем регулирования по термогазодинамическим параметрам в качестве исходных используются основные уравнения рабочего процесса, известные из теории ГТД [32, 33]. Проиллюстрируем это на примере двух простейших уравнений: уравнения, связывающего отношения давлений в узлах двигателя, и уравнения баланса мощностей турбины и компрессора. Уравнение, связывающее отношения давлений в разных сечениях двигателя, имеет следующий вид: 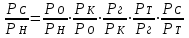 , ,где Рн - давление в невозмущенном потоке; Ро - давление на входе в компрессор двигателя; Рк - давление за компрессором двигателя; Рг - давление перед турбиной; Рт - давление за турбиной; Рс - давление на срезе сопла. Обозначив соответствующие отношения давлений через значения степени повышения или понижения давления и через коэффициенты восстановления давления , это уравнение можно переписать в следующем виде: 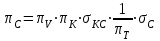 . .Это уравнение нелинейное и выражается через произведение сомножителей. Поэтому для его линеаризации необходимо провести сначала логарифмирование, затем дифференцирование и далее соответствующие преобразования (см. первый вариант линеаризации). Если рассматривается работа двигателя на земле, то можно считать V = const. Выполнив необходимые преобразования, получим линейное алгебраическое уравнение в относительных отклонениях: 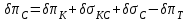 . .Данное уравнение устанавливает связь между относительными изменениями параметров, характеризующих техническое состояние компрессора - 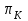 , турбины - , турбины - 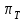 , камеры сгорания - , камеры сгорания - 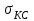 , сопла - , сопла - 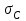 . . Уравнение баланса мощностей на валу двигателя устанавливает соотношение между работой турбины |