2. Молекулярная (статистическая) физика и термодинамика 2 Средняя энергия молекул
Число степеней свободы: 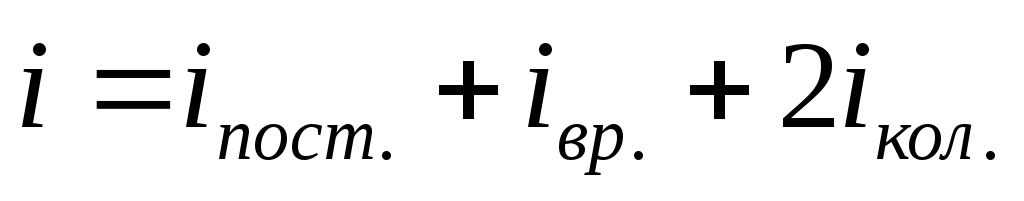
Основное уравнение молекулярно-кинетической теории:  . .
Связь давления с температурой тела: 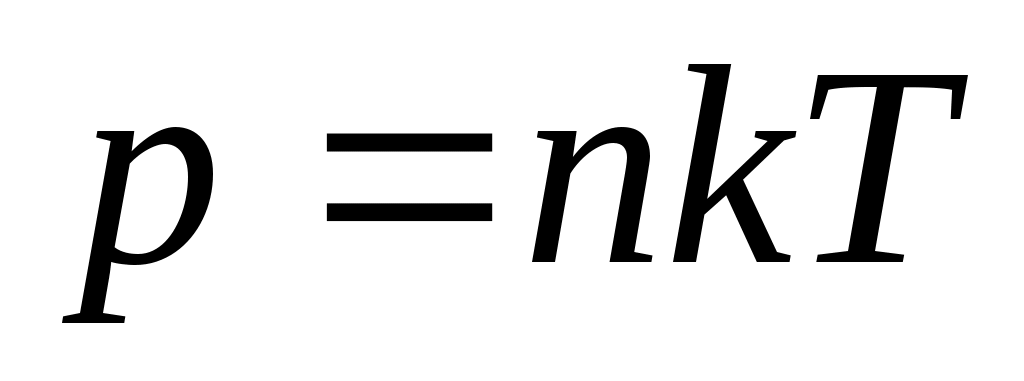 . .
2.2.1-1
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. Средняя кинетическая энергия молекул гелия (Не) равна …
|
1. 
2. 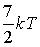
3. 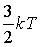 * *
4. 
|
Основное уравнение кинетической теории газов: где р – давление газа, n – число молекул в единице объема (концентрация молекул), где р – давление газа, n – число молекул в единице объема (концентрация молекул), 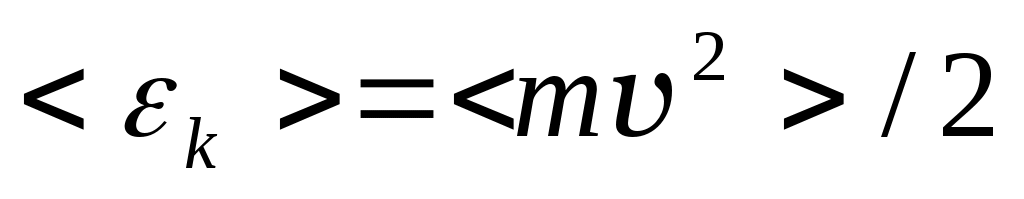 – средняя кинетическая энергия поступательного движения одной молекулы. Числом степеней свободы i называется число независимых величин, с помощью которых может быть описано состояние молекулы. Существует 3 поступательные, 3 – вращательные степени свободы (для двухатомного газа – 2), колебательные степени свободы учитываются редко. Для молекул одноатомного газа i=3; двухатомного газа i=5, трех- и более атомных газов i=6. – средняя кинетическая энергия поступательного движения одной молекулы. Числом степеней свободы i называется число независимых величин, с помощью которых может быть описано состояние молекулы. Существует 3 поступательные, 3 – вращательные степени свободы (для двухатомного газа – 2), колебательные степени свободы учитываются редко. Для молекул одноатомного газа i=3; двухатомного газа i=5, трех- и более атомных газов i=6.
Средняя кинетическая энергия, приходящаяся на одну степень свободы молекулы 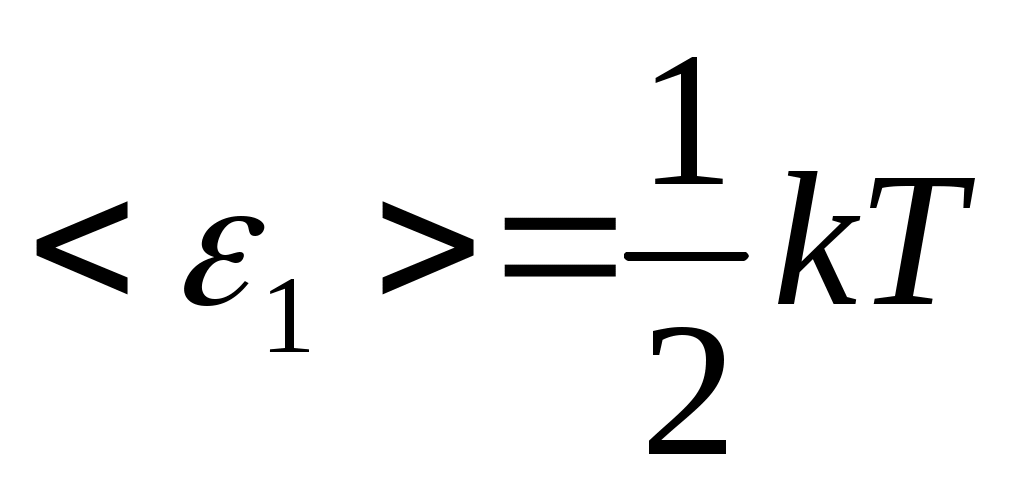 . Средняя кинетическая энергия, приходящаяся на все степени свободы молекулы (полная энергия молекулы) . Средняя кинетическая энергия, приходящаяся на все степени свободы молекулы (полная энергия молекулы)  Средняя кинетическая энергия поступательного движения молекулы: Средняя кинетическая энергия поступательного движения молекулы:  Средняя кинетическая энергия вращательного движения молекулы: Средняя кинетическая энергия вращательного движения молекулы: 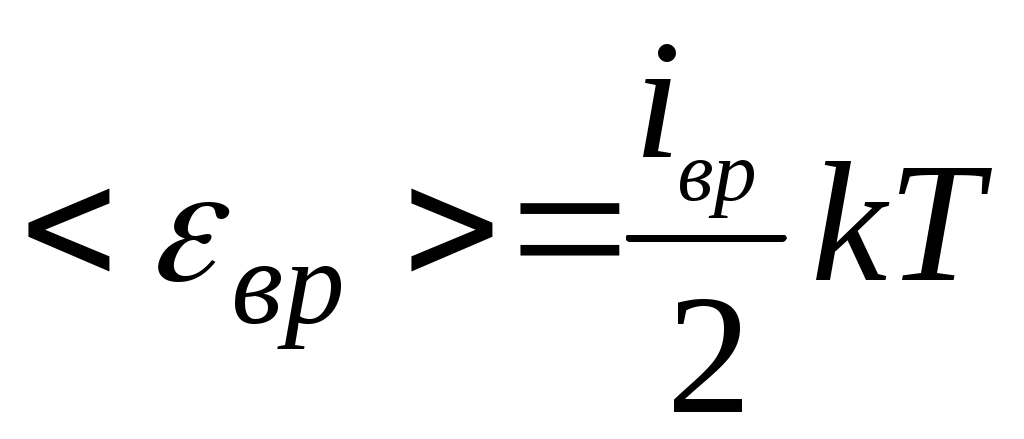 . Молекула гелия – одноатомный газ, следовательно, число степеней свободы i=3, следовательно, средняя кинетическая энергия . Молекула гелия – одноатомный газ, следовательно, число степеней свободы i=3, следовательно, средняя кинетическая энергия  . .
Ответ: 3
2.2.1-2
На каждую степень свободы движения молекулы приходится одинаковая энергия, равная 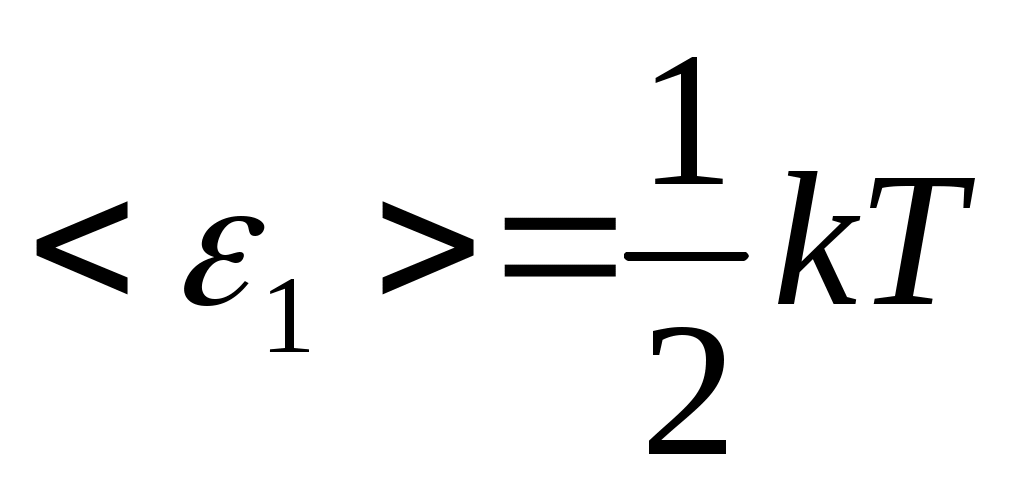 (k – постоянная Больцмана, Т – температура по шкале Кельвина). При условии, что имеют место все виды движения, средняя кинетическая энергия молекулы водорода (Н2) равна … (k – постоянная Больцмана, Т – температура по шкале Кельвина). При условии, что имеют место все виды движения, средняя кинетическая энергия молекулы водорода (Н2) равна …
|
1. 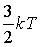
2. 
3. 
4. 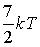 * *
|
Т.к. средняя кинетическая энергия, приходящаяся на все степени свободы молекулы (полная энергия молекулы)  , i–число степеней свободы молекулы водорода (Н2), равное 7, т.к. Н2 – двухатомный газ и имеют место все виды движения: , i–число степеней свободы молекулы водорода (Н2), равное 7, т.к. Н2 – двухатомный газ и имеют место все виды движения: 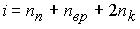 , , 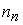 =3 (поступательное движение), =3 (поступательное движение), 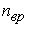 =2 (вращательное для линейной молекулы), =2 (вращательное для линейной молекулы),  =3N-5 = 1. =3N-5 = 1.
Ответ: 4
2.2.1-3
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место все виды движения, средняя энергия молекул азота (N2) равна …
|
1: 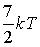 * *
2: 
3: 
4: 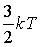
|
Т.к. средняя кинетическая энергия, приходящаяся на все степени свободы молекулы (полная энергия молекулы)  , i – число степеней свободы молекулы водорода (N2) равное 7, т.к. N2 – двухатомный газ и имеют место все виды движения: , i – число степеней свободы молекулы водорода (N2) равное 7, т.к. N2 – двухатомный газ и имеют место все виды движения: 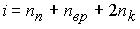 , , 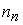 =3 (поступательное движение), =3 (поступательное движение), 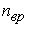 =2 (вращательное для линейной молекулы), =2 (вращательное для линейной молекулы),  =3N-5=1. =3N-5=1.
Ответ: 1
2.2.1-4
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул азота (N2) равна …
|
1:  * *
2: 
3: 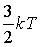
4: 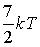
|
Т.к. средняя кинетическая энергия, приходящаяся на все степени свободы молекулы (полная энергия молекулы)  , i – число степеней свободы молекулы водорода (N2) равное 5, т.к. N2 – двухатомный газ и имеют место только поступательное и вращательное виды движения: , i – число степеней свободы молекулы водорода (N2) равное 5, т.к. N2 – двухатомный газ и имеют место только поступательное и вращательное виды движения: 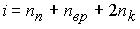 , , 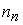 =3 (поступательное движение), =3 (поступательное движение), 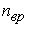 =2 (вращательное для линейной молекулы). =2 (вращательное для линейной молекулы).
Ответ: 1
2.2.1-5
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул водяного пара (H2O) равна …
|
1: * *
2: 
3: 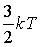
4: 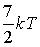
|
Т.к. молекулы водяного пара (H2O) состоят из трех атомов. Нежесткая нелинейная трехатомная молекула имеет три колебательные степени свободы, три поступательные и три вращательные. Т.к. имеют место только поступательные и вращательные, то i=6. По формуле  средняя энергия молекул водяного пара (H2O) средняя энергия молекул водяного пара (H2O)  . .
Ответ: 1
2.2.1-6
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул метана (CH4) равна …
|
1: * *
2: 
3: 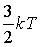
4: 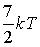
|
Т.к. молекулы водяного пара (CH4) состоят из пяти атомов. Имеет место три колебательные степени свободы, три поступательные и три вращательные степени свободы. Т.к. имеют место только поступательные и вращательные, то i=6. По формуле  средняя энергия молекул водяного пара (CH4) средняя энергия молекул водяного пара (CH4)  . .
Ответ:1
2.2.1-7
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул углекислого газа (CO2) равна … (Учесть, что молекула CO2 – линейная)
|
1:  * *
2: 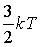
3: 
4: 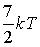
|
Т.к. молекулы водяного пара (CO2) состоят из трех атомов, при условии, что молекула углекислого газа линейна, то молекула имеет 3 поступательные и 2 вращательные степени свободы, таким образом, число степеней свободы 5. По формуле  средняя энергия молекул водяного пара (CO2) средняя энергия молекул водяного пара (CO2)  . .
Ответ: 1
2.2.2-1
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 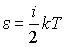 . Здесь . Здесь 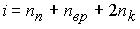 , где , где 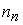 , , 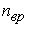 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для гелия (Не) число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для гелия (Не) число i равно …
|
1. 7
2. 3*
3. 1
4. 5
|
Гелий – одноатомный газ, поэтому число степеней свободы i=3.
Ответ: 2
2.2.2-2
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 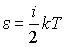 . Здесь . Здесь 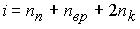 , где , где 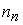 , , 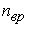 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для атомарного водорода число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для атомарного водорода число i равно …
|
1. 3*
2. 1
3. 5
4. 7
|
Атомарный водород – одноатомный газ, поэтому число степеней свободы i=3.
Ответ: 1
2.2.2-3
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 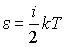 . Здесь . Здесь 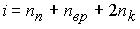 , где , где 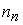 , , 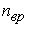 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место все виды движений, для водорода (Н2) число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место все виды движений, для водорода (Н2) число i равно …
|
1: 7*
2: 2
3: 5
4: 8
|
Водород (Н2) – двухатомный газ, 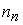 =3 (поступательное движение); =3 (поступательное движение); 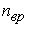 =2 (вращательное для линейной молекулы); =2 (вращательное для линейной молекулы);
 =3N-5=1 (N – число атомов в молекуле). Таким образом, получаем i=3+2+2*1=7 =3N-5=1 (N – число атомов в молекуле). Таким образом, получаем i=3+2+2*1=7
Ответ: 1
2.2.2-4
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 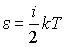 . Здесь . Здесь 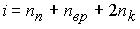 , где , где 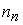 , , 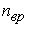 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водорода (Н2) число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водорода (Н2) число i равно …
|
1: 5*
2: 2
3: 8
4: 7
|
Водород (Н2) – двухатомный газ, поэтому число степеней свободы i=5: 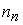 =3 (поступательное движение), =3 (поступательное движение), 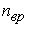 =2 (вращательное движение для линейной молекулы). =2 (вращательное движение для линейной молекулы).
Ответ:1
2.2.2-5
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 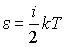 . Здесь . Здесь 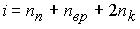 , где , где 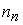 , , 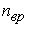 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
|
1: 6*
2: 3
3: 5
4: 8
|
Водяной пар (Н2O) – трехатомный газ, поэтому число степеней свободы i = 6: 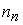 =3 (поступательное движение), =3 (поступательное движение), 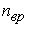 =3 (вращательное движение). =3 (вращательное движение).
Ответ: 1
2.2.2-6
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 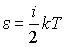 . Здесь . Здесь 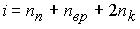 , где , где 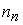 , , 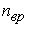 и и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для углекислого газа (CO2) с учетом того, что молекула CO2 – линейная, и имеют место все виды движения число i, равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для углекислого газа (CO2) с учетом того, что молекула CO2 – линейная, и имеют место все виды движения число i, равно …
|
1: 7*
2: 3
3: 5
4: 8
|
Молекула CO2 – линейная, состоит из трех атомов, поэтому: 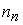 =3 (поступательное движение), =3 (поступательное движение), 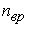 =2 (вращательное для линейной молекулы), =2 (вращательное для линейной молекулы),  =3N-5=1. Таким образом, получаем i=7. =3N-5=1. Таким образом, получаем i=7.
Ответ: 1
2.2.2-7
Средний импульс молекулы идеального газа при уменьшении абсолютной температуры газа в 4 раза …
|
1. увеличится в 4 раза
2. уменьшится в 4 раза
3. уменьшится в 2 раза*
4. не изменится
5. увеличится в 2 раза
|
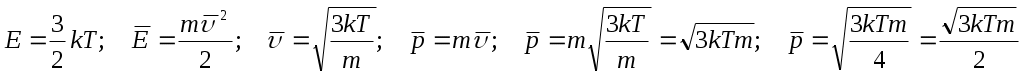
Следовательно, при уменьшении абсолютной температуры газа T в 4 раза, средний импульс молекулы уменьшится в 2 раза.
Ответ: 3 |
 Скачать 145 Kb.
Скачать 145 Kb.