Лекция 2 часть 1 Потенциал (полная версия). 2. Потенциал электростатического поля. Пионером
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
2. Потенциал электростатического поля. («Пионером» в этой области считается Лагранж, который в 1777 году впервые ввел понятие потенциала для гравитационного поля). 2.1. Работа сил электростатического поля по переносу точечного заряда. 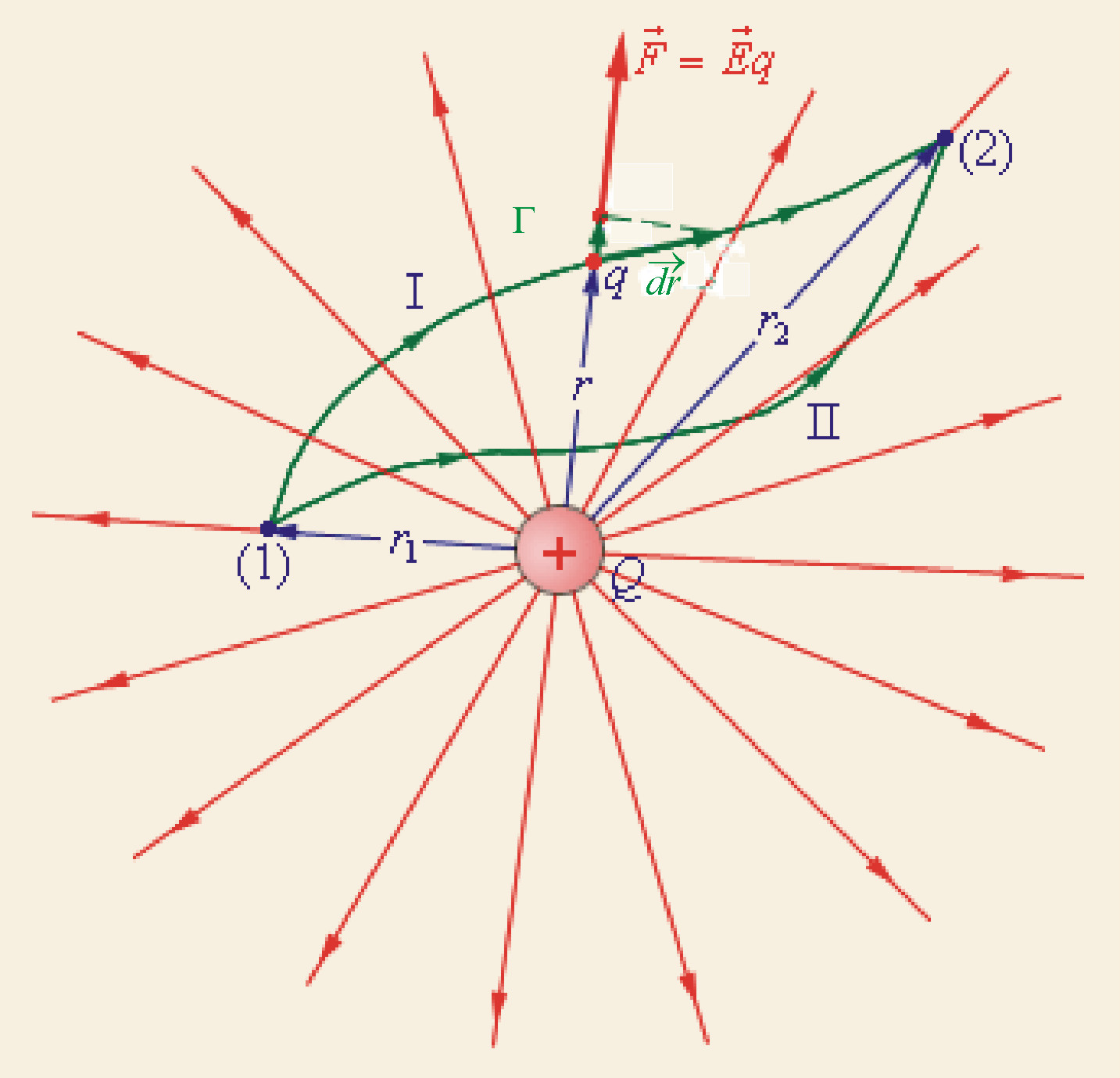 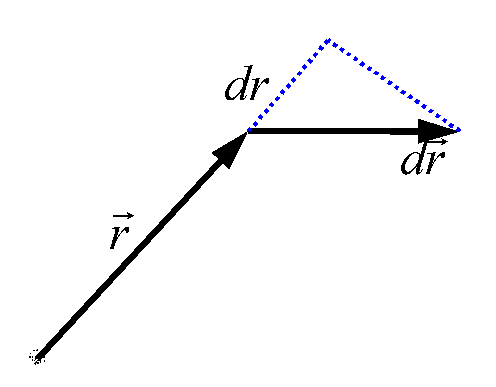 Пробный (положительный и очень маленький по размеру – это определение пробного заряда) заряд q медленно (квазистатически – заряд находится почти в покое) перемещаем по пути Г («гамма-большое») из 1 в 2 в электростатическом поле точечного статического заряда Q. Найдем элементарную работу сил электростатического поля этого заряда по перемещению заряда q: Как известно из курса механики Элементарная работа силы 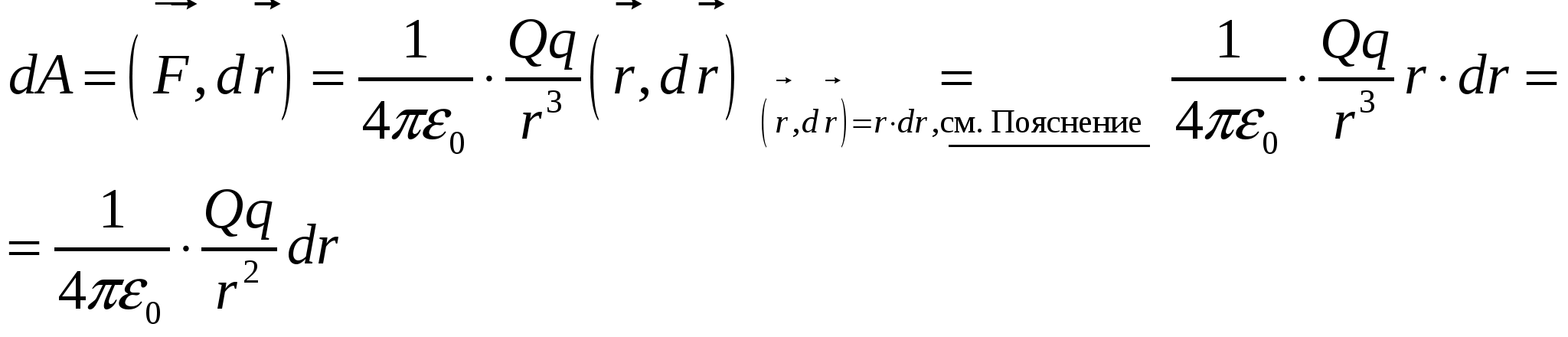 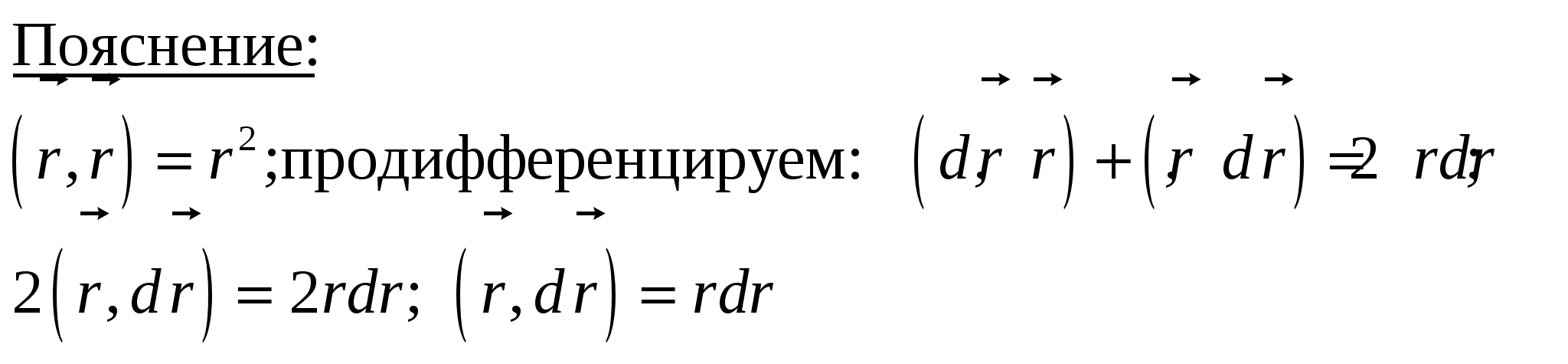 Итак, работа сил электростатического поля по перемещению точечного заряда из положения 1 в положение 2 по контуру Г может быть вычислена по формуле: Итак, работа сил электростатического поля по перемещению точечного заряда из положения 1 в положение 2 по контуру Г может быть вычислена по формуле: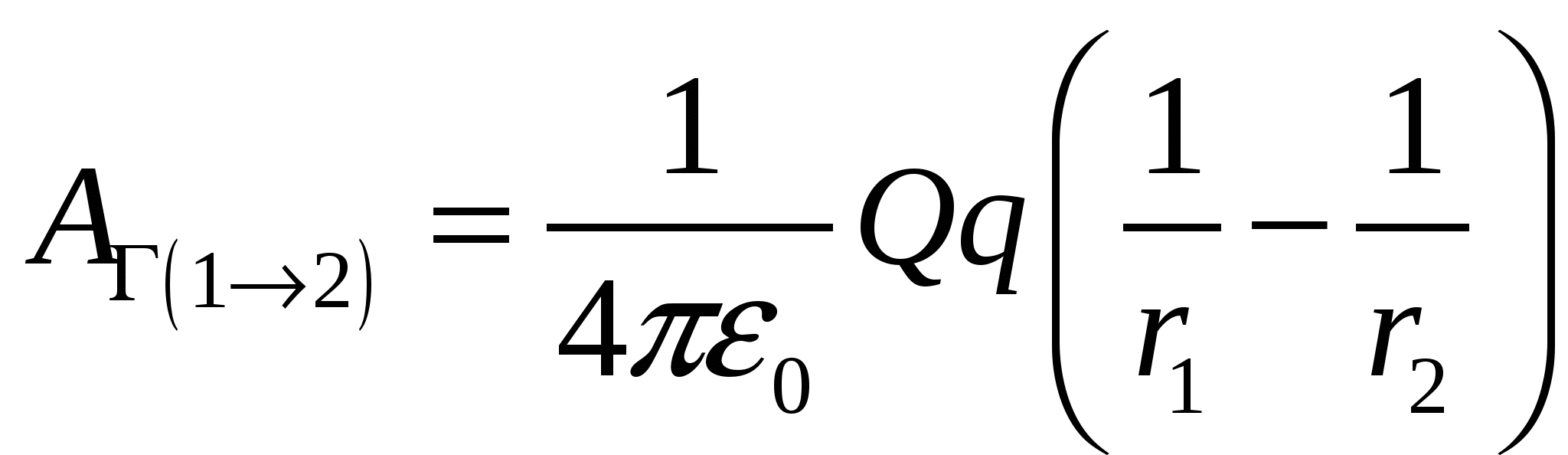 (1) (1)2.2. Интегральный признак потенциальности электростатического поля. Анализируя полученную формулу для работы сил электростатического поля по перемещению заряда q по некоторому контуру Г, можно сделать следующие выводы:
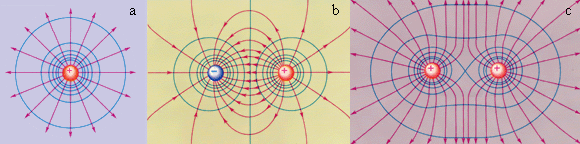
Линейный интеграл, взятый по замкнутому контуру (замкнутой кривой) Г, называется циркуляцией вектора Последний результат справедлив и для электростатического поля, созданного любой системой покоящихся точечных зарядов, т.к. по принципу суперпозиции электростатических полей Векторное поле называется потенциальным, если циркуляция этого вектора по любому замкнутому контуру Однако этот критерий потенциальности является неудобным на практике, т.к. нужно будет исследовать всевозможные контуры (что само по себе невозможно), и установить, является ли интеграл по ним равным нулю. 2.3. Локальный (дифференциальный) признак потенциальности электростатического поля. Н 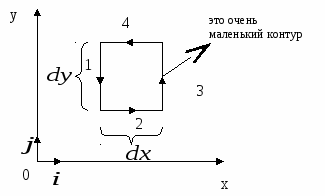 айдем циркуляцию вектора айдем циркуляцию вектора Т.к. величины dx и dyявляются очень маленькими, можно считать, что и поле на протяжении этих отрезков также одинаково; будем обозначать поле в каждой точке стороны 1 как 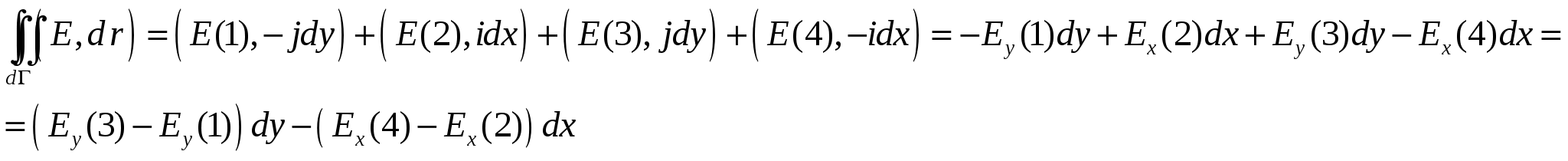 Теперь заметим, что выражение 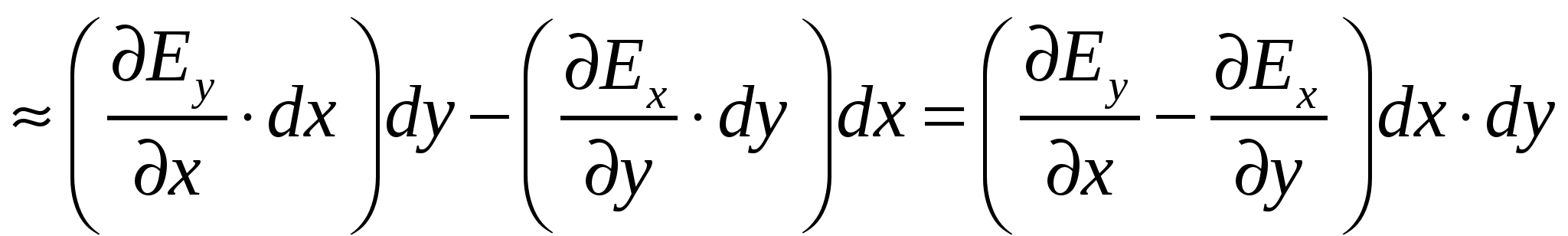 Мы нашли циркуляцию вектора Аналогично для элементарных прямоугольных контуров в плоскостях yzи zx можно получить: 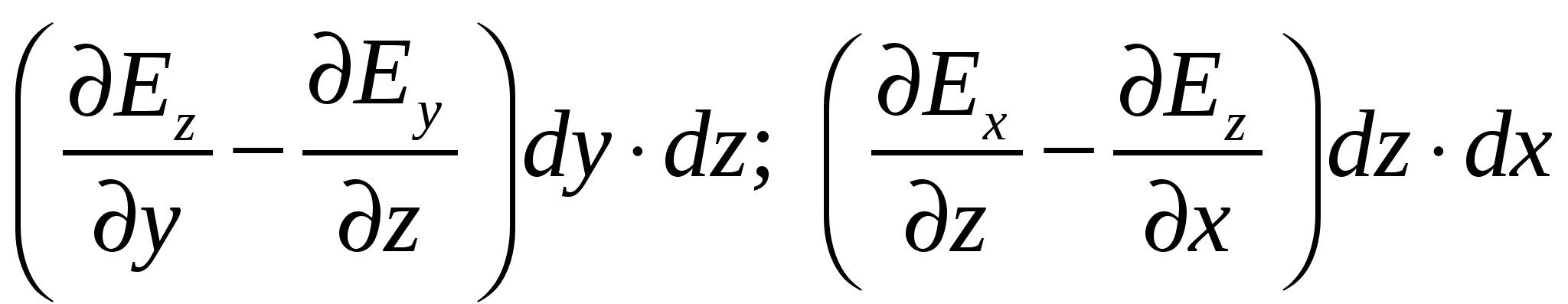 А так как циркуляция вектора То, что выписано – необходимый, а в электростатике – и достаточный признак потенциальности электрического поля в декартовой системе координат. Выполнение этих равенств проверить на практике гораздо проще, чем проверять интегральный признак потенциальности электростатического поля. Итак, поле Условия (*) можно компактно записать в векторной форме, если ввести в рассмотрение вектор "ротор" напряженности электрического поля (см. Замечание). Ротор вектора Векторное произведение вектора оператора градиента и вектора напряженности электрического поля, или ротор 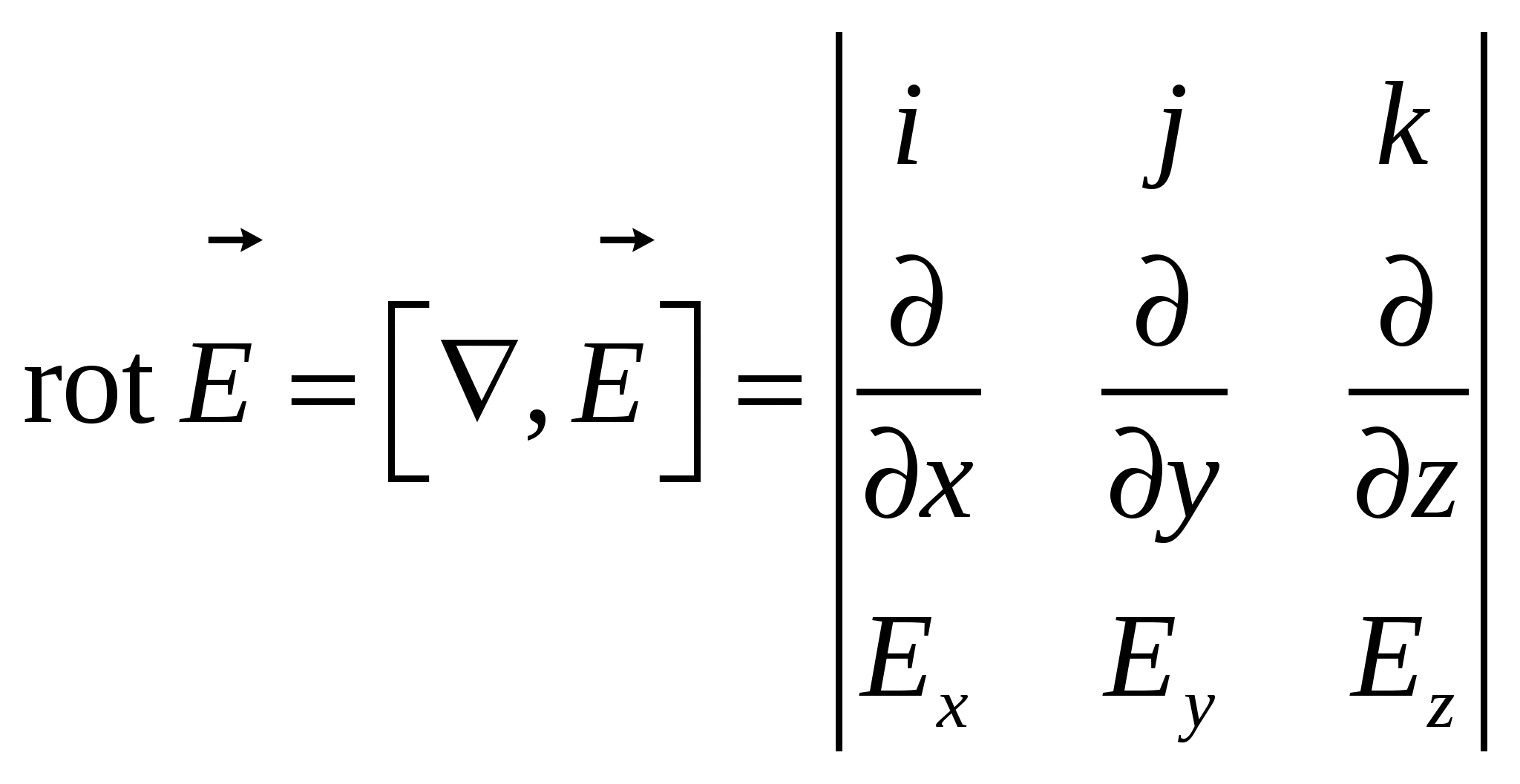 Следовательно, для электростатического поля имеем ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. 2.4 Определение потенциала. Интегральное соотношение между Потенциальное поле векторов Разность потенциалов 2.5. Нормировка потенциала или выбор уровня отсчета. Перепишем формулу (3) иначе: Существуют два удобных способа выбора значения аддитивной постоянной. 1. Если система зарядов занимает ограниченную область пространства, то потенциал бесконечно удаленной точки обычно полагают равным нулю. Потенциал любой другой точки согласно однозначно определится выражением 2. В практике электрических измерений часто полагают равным нулю потенциал поверхности Земли. При этом исходят из того, что вследствие очень большой электрической емкости Земли ее потенциал практически неизменен и соединение какого-либо проводника с Землей (заземление) делает его потенциал практически фиксированным. В этом случае Когда говорят о потенциале, то имеют ввиду разность потенциалов Вообще, физический смысл имеет величина, которая может быть измерена. Поэтому говорят, что потенциал Потенциал характеризуется аддитивностью и он подчиняется принципу суперпозиции, как и вектор напряженности электрического поля. Если электрическое поле создано системой точечных зарядов, то потенциал С использованием разности потенциалов квазистатическая работа сил поля при перемещении заряда q0 по произвольному пути из точки 1 в точку 2 представится на основании (3) как т.е. квазистатическая работа сил поля равна убыли потенциала, умноженной на величину перемещаемого заряда. Единицей измерения потенциала служит вольт (В). Если между двумя точками пространства для переноса заряда в один кулон требуется совершить работу в один джоуль, то разность потенциалов в этих точках равна одному вольту. 2.6. Локальное (дифференциальное) соотношение между Рассмотрим 2 близкие точки 1 и 2 на координатной оси OX в электростатическом поле Получается, что Если точки 1 и 2 лежат в произвольной точке пространства, то аналогичное соотношение можно получить для проекции напряженности на другие оси декартовой системы координат: Таким образом, вектор (читается так: «Набла фи»). 2.7. Физический смысл градиента (подробно прочитать- литература 6, стр.80-82)Рассмотрим приращение потенциала d Здесь 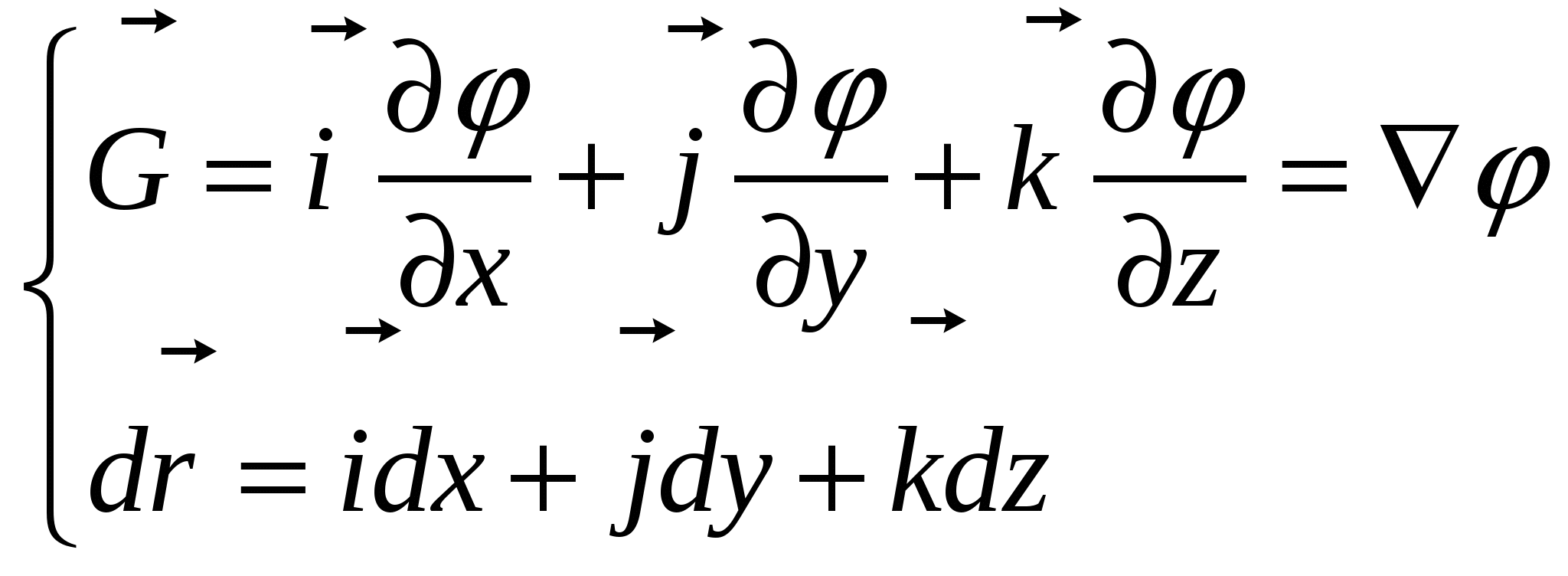 Рассмотрим величину d 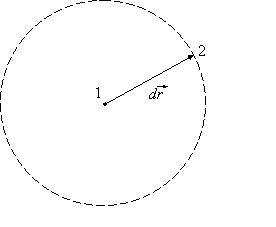 Рис.1. Элементарный вектор видно, что максимальная величина 1) направление вектора градиента потенциала указывает направление наиболее быстрого возрастания поля 2) величина вектора 3) “скорость” пространственного изменения потенциала в произвольном направлении (задаваемом вектором На основании изложенного выше и выражения (5) приходим к следующему утверждению. Вектор поля Введем понятие эквипотенциальной поверхности - поверхности, во всех точках которой потенциал имеет одно и то же значение. Выделим поверхность одинакового потенциала 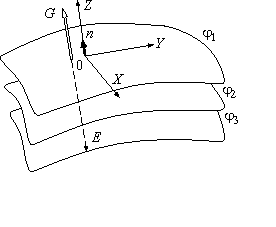 Рис. 2. Взаимное расположение трех эквипотенциальных поверхностей ( По построению т.е. вектор градиента поля, а значит, и вектор Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электростатического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. Д 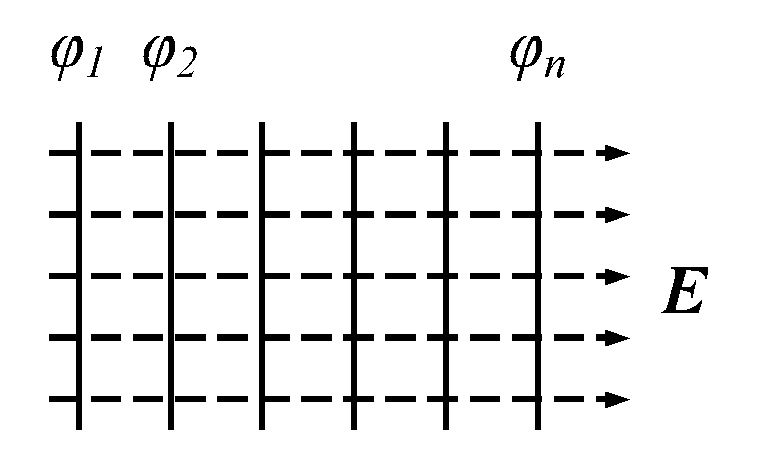 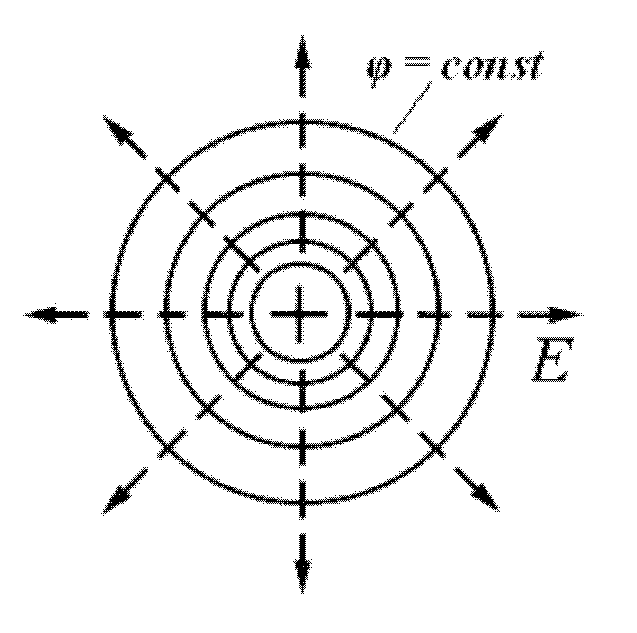 ля однородного поля эквипотенциальные поверхности параллельные линии. ля однородного поля эквипотенциальные поверхности параллельные линии. На рис. представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
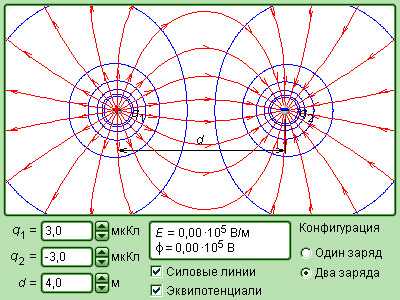
Вопрос из ОРОКСА Две линии напряженности электрического поля не могут пересекаться в одной точке. Можно ли утверждать, что две эквипотенциальные поверхности также не могут пересекаться в одной точке? Ответ: Две эквипотенциальные поверхности могут пересекаться в одной точке при условии, что напряженность поля в этой точке равна нулю. В самом деле, вектор напряженности определяет направление нормали к каждой эквипотенциальной поверхности. Так как поверхности пересекаются, в точке пересечения их нормали не совпадают, а значит, электрическое поле не может иметь определенного направления. Это возможно только при нулевом значении величины поля. Модель 1.2. Электрическое поле точечных зарядов
Компьютерная модель демонстрирует картину силовых линий и эквипотенциальных поверхностей точечного заряда и системы из двух точечных зарядов. Можно изменять величины зарядов и их знаки, а также расстояние между зарядами. При установке курсора в любой точке и нажатии левой клавиши мыши компьютер высвечивает на дисплее значения модуля вектора напряженности электрического поля 2.7. Примеры вычисления потенциалаРассмотрим вычисление потенциала поля, созданного некоторыми заряженными телами. 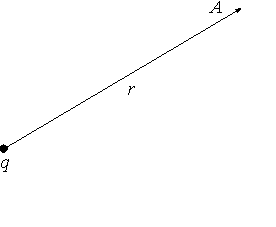 Рис.3. Расположение точки наблюдения А по отношению к точечному источнику поля q 1. Пример Точечный заряд. Используя соотношения (1) и (4) и совмещая точку 1 с точкой наблюдения А (рис.3), а точку 2 удаляя на бесконечность, получим Замечание. До сих пор использовалось понятие векторного поля - поля векторов 2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью Наша задача найти К  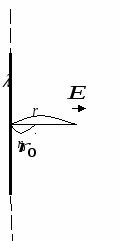 ак уже было показано для бесконечно длинной нити: ак уже было показано для бесконечно длинной нити:Выберем где-нибудь точку из которой мы стартуем, к примеру в точке Договоримся, что в точке старта потенциал равен нулю: Это при такой нормировке. Если в такой задаче нормировать 3.Пример. Потенциал поля точечного диполя (первый способ). И 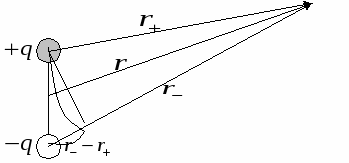 так, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки. так, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.Давайте искать потенциал этой точки наблюдения. Во первых, принцип суперпозиции. Во-вторых, как известно Учтя, что  Потенциал поля точечного диполя (второй способ). Используем готовую формулу для напряженности поля: 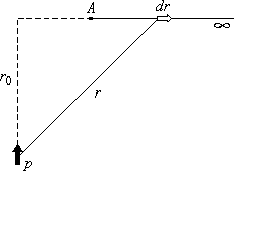 Д 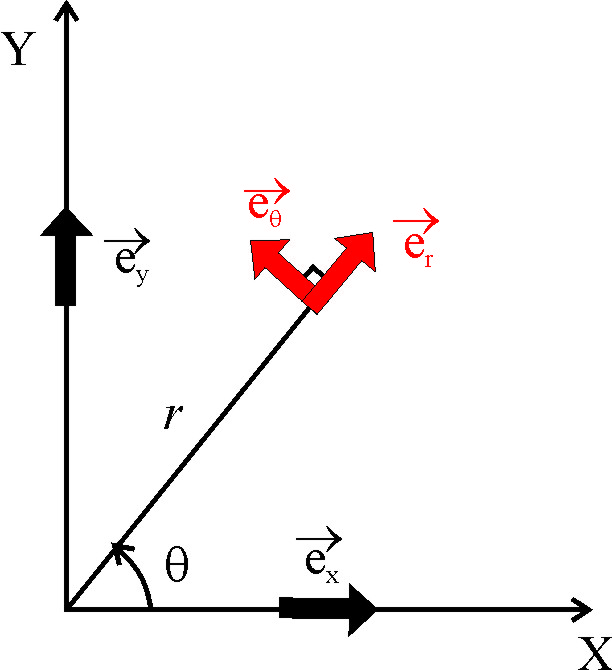 авайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор авайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор Определение вектора Орты координатных осей декартовой и полярной систем координат (см.рис.) 4.Пример См. Иродов задача 3.38. (часть2) Показать, что потенциал диполя с электрическим моментом может быть представлен как 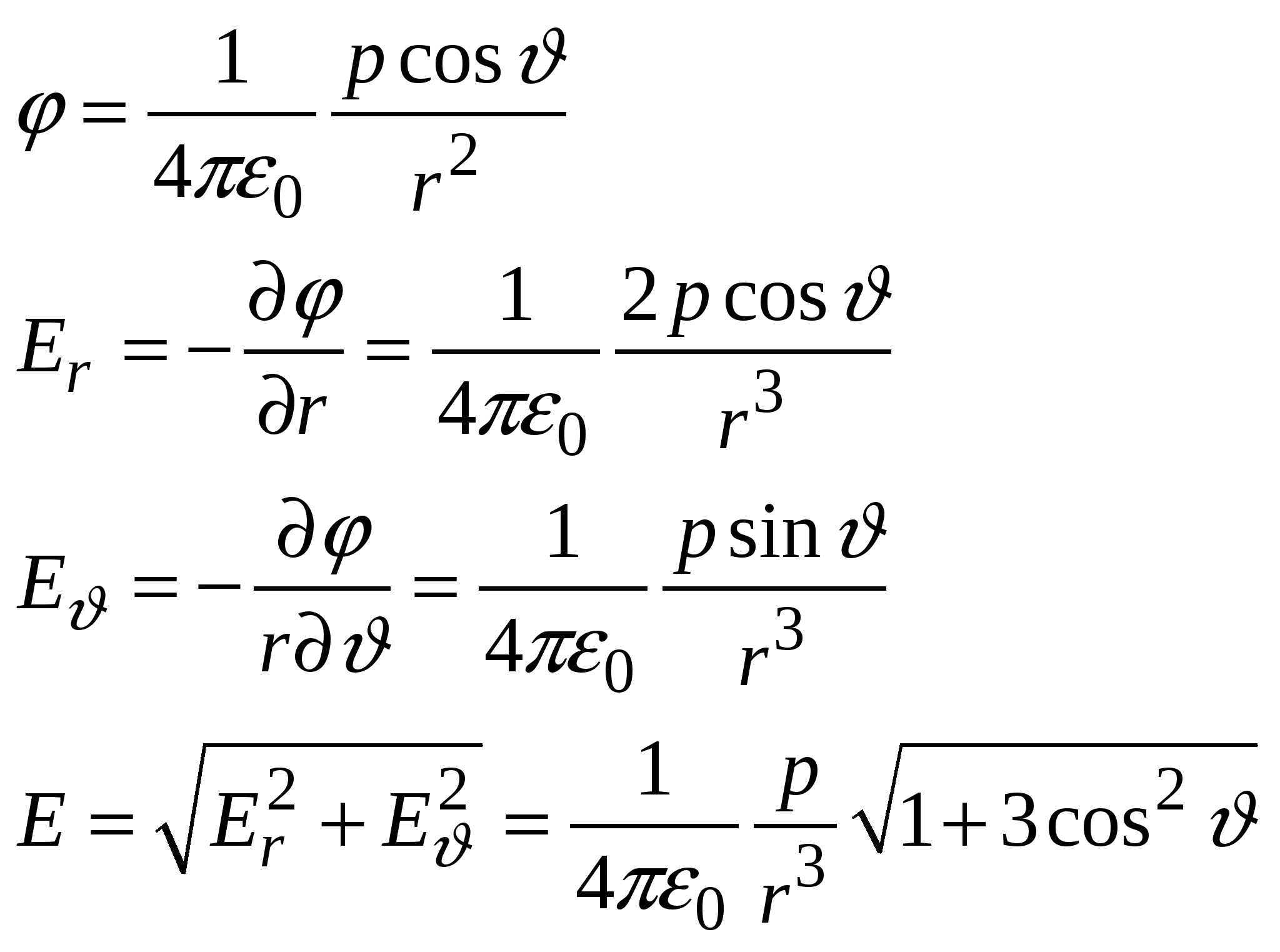 Сводка формул к лекции 2 ОПЫТЫ И КОМЬЮТЕРНЫЕ ДЕМОНСТРАЦИИЭлементарная электростатика Электризация трением Электризация трением Электризация через влияние Электризация через влияние Взаимодействие точечных зарядов Взаимодействие точечных зарядов Электростатическая машина Электростатическая машина Генератор Ван-де-Граафа Генератор Ван-де-Граафа Электрический ветер Электрический ветер |