Механика расчет зубчатого колеса. 2 Проектный расчет передачи

• Название: 2 Проектный расчет передачи
• Анкор: Механика расчет зубчатого колеса
• Дата: 18.01.2023
• Размер: 155.5 Kb.
• Имя файла: 4-1.doc
• Тип: Документы; #892029

2.2. Проектный расчет передачи
Межосевое расстояние определим из условия контактной прочности (4.1 [1]):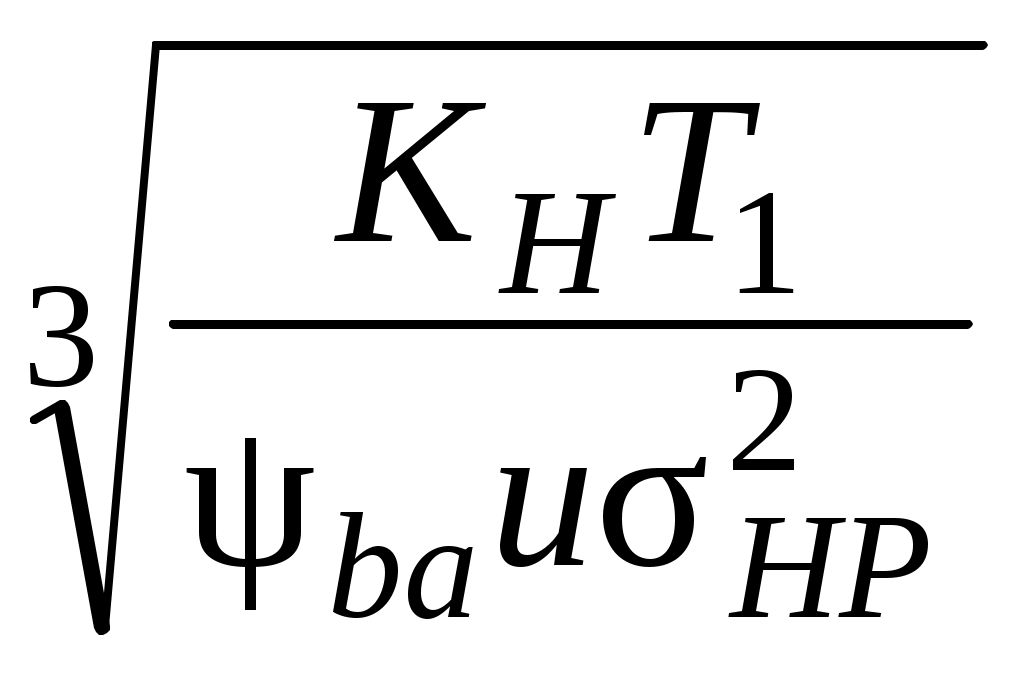

= (u 1) ,

где K_a = - коэффициент вида передачи,

ψ_ba - коэффициент ширины венца по межосевому расстоянию, выбираем из ряда на с.10 [1] с учетом расположения опор относительно зубчатого венца ψ_ba=0.4;

K_Н  коэффициент контактной нагрузки, принимаем на этапе проектного расчета K_Н =1.2.

Расчетное межосевое расстояние:

= (3.55 + 1) [1.2·372,45 Н*м / (0.4·3.55·494² МПа)] = 203,34 мм.

Полученную величину округлим до ближайшего стандартного значения (табл.6.1 [1]): = 200 мм.

Находим ширину колеса и шестерни по формулам:

b_w2 = ψ_ba = 0.4·200 мм = 80 мм;

b_w1 = b_w2 + 5 мм= 80 мм + 5 мм = 85 мм.

Полученные значения округляем по ряду нормальных линейных размеров (c.12 [1]): b_w1 = 85 мм, b_w2 = 80 мм.

Коэффициенты смещения: шестерниx₁= , колеса x₂= , суммарный x = .

Модуль выбираем из диапазона m = и округляем до стандартного значения по ГОСТ 9563-60 (табл.5.1 [1]), учитывая, что применение модуля меньше 2 мм для силовых передач не рекомендуется.

m = 0,015 * 200 = 3 мм

Окончательно примем m= 3 мм.

Для косозубых передач стандартизован нормальный модуль m_n = m.

Суммарное число зубьев: Z = ,

где ₁ – начальный делительный угол наклона зуба, ₁=12º.

В результате расчета получили:

Z = (2· мм ·cos12º)/ 3 мм = 130,4.

Округлили Z до ближайшего целого числа: Z_Σ = 130.

Делительный угол наклона зуба определили по формуле

= arccos [130·3/ (2·200 мм)] = 12,84º.

Число зубьев шестерни, колеса и уточненное передаточное число равны: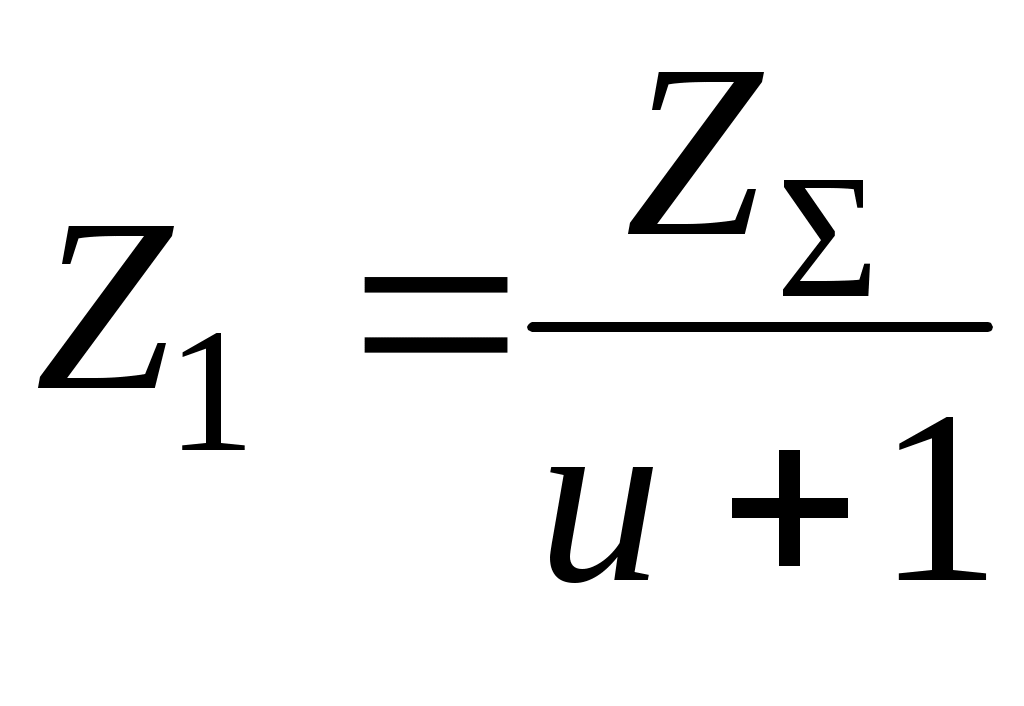

= 28,88, после округления получили Z₁ = 29,

Z₂ = Z – Z₁ = 101;

u_ф = = 3,48.

Определение диаметров окружностей зубчатых колес.

Делительные окружности: d_j= ,

d₁ = 3 мм·29/cos 12,84º = 89 мм;

d₂ = 3 мм·101/cos 12,84º = 311 мм.

Окружности впадин зубьев d_fj = d_j– 2 m (1.25 – x_j),

d_f1 = 89 мм – 2·3 мм (1.25 – ) = 81.5 мм;

d_f2 = 311 мм – 2·3 мм (1.25 – ) = 303.5 мм.

Окружности вершин зубьев

d_a1 = 2 a_w – d_f2 – 0.5m = 2· мм – 303.5 мм – 0.5·3 мм = 95 мм;

d_a2 = 2 a_w – d_f1 – 0.5m = 2·200 мм – 81.5 мм – 0.5·3 мм = 317 мм.

Окружная скорость в зацеплении

V= = π 89·216.27/ 60000 = 1,007 м/с.

По табл.8.1 [1] для полученной скорости V назначаем степень точности передачи n_cт = 8. (степень точности передачи меньше 8 не назначать!)
2.3. Проверочный расчет передачи
2.3.1. Проверка на выносливость по контактным напряжениям
Определим контактные напряжения по формуле (с.14 [1])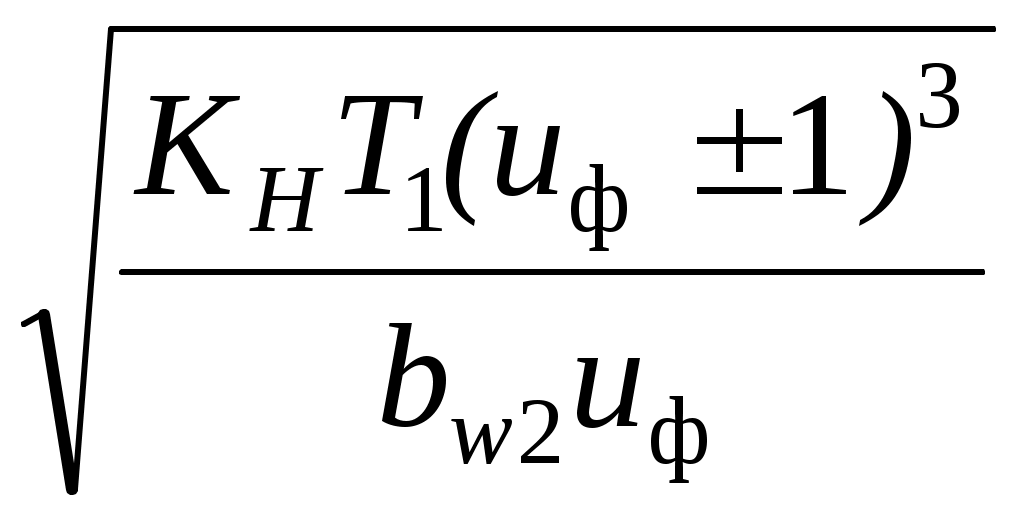

= ,

где Z = 8400 - коэффициент вида передачи для прямозубой передачи;

K_H  коэффициент контактной нагрузки, K_H = K_Hα K_Hβ K_HV.

Коэффициент неравномерности распределения нагрузки между зубьями равен:

K_Hα =1+ A (n_ст – 5) K_w,

где A = 0,15 для прямозубой передачи; K_w- коэффициент, учитывающий приработку зубьев. Величину K_w определяют по формуле:

K_w= 0.002 НВ₂ + 0.036 (V – 9) = 0.002·248.5 МПа + 0.036 (1,007 м/с – 9) = 0.209.

При НВ₂>350 принимают K_w=1.

В результате расчета получим: K_Hα = 1+ 0.15( – 5) 0,209 = 1,09.

Динамический коэффициент определим по табл.10.1 [1]: K_НV = 1,02.

Коэффициент неравномерности распределения нагрузки по ширине колеса

K_Hβ = 1+ (K – 1) K_w,

где K =1.035 – значение коэффициента K_Hβ в начальный период работы (табл.9.1 [1]).

В таблице значение K дано в зависимости от коэффициента ширины венца по диаметру , величина которого определяется выражением:

= 0.5 (u + 1) = 0.5·0,4 (3.55 + 1) = 0,91.

Окончательно получим:

K_Hβ = 1+ (K – 1)K_w =1 + (1.035 – 1) · 0,209 = 1,007;

K_H= 1,09 ·1,007·1,02 = 1,12

Расчетные контактные напряжения:

_H = (8400/ 200 мм) [1,12·372,45 Н*м (3,48 + 1)³]/( 80 мм·3,48)] = 487,5 МПа.

Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%. Расчет недогрузки выполним по формуле

=100 =100 (515,45 МПа – 487,5 МПа) / 515,45 МПа = 0,05 %.
2.3.2. Проверка на выносливость по напряжениям изгиба
Проверочный расчет на выносливость при изгибе зубьев шестерни и колеса выполним по формулам (c.15 [1]):

; ,

где Y_Fj  коэффициенты формы зуба (с.16 [1])

Y_Fj = 3.47 + + 0.092 ;

здесь Z_Vj = - эквивалентное число зубьев;

Y_  коэффициент, учитывающий влияние угла наклона зуба на его прочность,

= 1– 0.01·12,8º= 0,87;

Y - коэффициент, учитывающий перекрытие зубьев, Y = для непрямозубых передач.

Коэффициент торцевого перекрытия определим по формуле (с.16 [1])

=[1.88 – 3.2 ( + )] cos =[1.88 – 3.2 (1/ 29 + 1/101)] cos 12,8º = 1,694.

В результате расчетов получим:

Z_V1 = 29 / cos³ (12,8º) = 31,28;

Z_V2= 101 / cos³ (12,8º) = 108,95;

Y_F1= 3.47+ (13.2 – 27.9·)/ 31,28 + 0.092·² = 3,892;

Y_F2 = 3.47+ (13.2 – 27.9·)/ 108,95+ 0.092·² = 3,591;

Y = 0,59.

Коэффициент нагрузки при изгибе равен

K_F = K_Fα K_Fβ K_FV.

Входящие в эту формулу коэффициенты, имеют такой же физический смысл, что и коэффициенты в формуле для K_Н. При их определении используют следующие зависимости:

K_Fα=1 + A (n_ст – 5) для непрямозубых передач,

K_Fβ = 0.18 + 0.82 K ,

K_FV = 1+1.5 (K_HV – 1) при НВ₂ <350

В результате расчетов получим

K_Fα =,45,

K_Fβ = 0.18 + 0.82·1,035 = 1,029;

K_FV = 1+ 1.5(1.134 - 1) = 1,03;

K_F = 1,45·1,029·1,03 = 1,537.

Расчетные напряжения изгиба

_F1=3,892·0,59·0,87·2000·372,45·1,537/(85·89·3) = 100,78 Мпа;

_F2= 100,78·85·3,591/(80·3,892) = 98,8 МПа.
2.4. Определение сил в зацеплении
Окружная сила: = 2000·372,45 / 89= 8370 Н.

Радиальная сила: = 8370 tg 20° / cos 12,8º = 3125 Н.

Осевая сила: F_a= F_t = 8370 tg 12,8º = 1900 Н.

Стр.