Датчик микросин взаимоиндуктивный. 7-микросин основа1 — копия. 2. Расчет статической характеристики преобразователя 1 Вывод функции преобразования. Расчет параметров магнитной цепи
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
 2.Расчет статической характеристики преобразователя 2.1 Вывод функции преобразования. Расчет параметров магнитной цепи. Выходное ЭДС преобразователя определяется в соответствии с методическим пособием [4]: 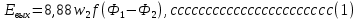 где f- частота напряжения питания, Гц; w2 – число витков сигнальной катушки; Ф1, Ф2 – магнитные потоки, проходящие через магнитный контур соответствующей сигнальной катушки, Вб. Совокупность путей прохождения (контуров) магнитного потока, создаваемого протекающими в катушках преобразователя токами, называется магнитной цепью. Задачей расчета магнитной цепи является вычисление магнитных потоков в различных частях магнитной системы, обусловленных наличием магнитодвижущей силы, создаваемой током катушки. В основу расчета магнитной цепи положены законы, которые по форме аналогичны законам электрической цепи. К этим законам относится закон Ома для магнитных цепей, первый и второй законы Кирхгофа. На рисунке 2 представлена эквивалентная схема замещения ИП с одной катушкой возбуждения, создающей магнитодвижущую силу, и располагаемой на центральном полюсе. 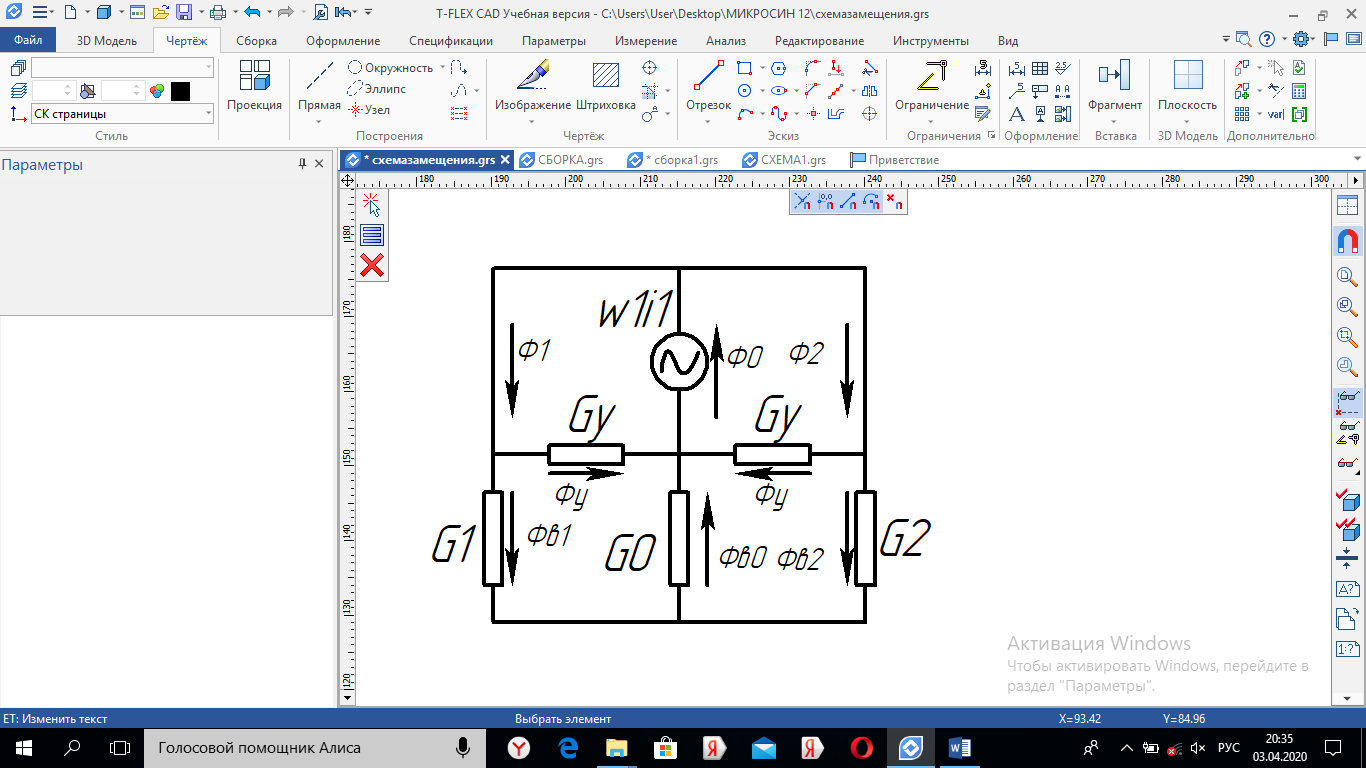 Рисунок 2- Схема замещения Для взаимоиндуктивного ИП с одной катушкой возбуждения, расположенной на центральном полюсе сердечника суммарная проводимость магнитной цепи будет равна: 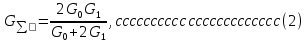 где G0 – проводимость воздушного зазора под центральным полюсом, [Гн]; G1 ,G2 – проводимость воздушного зазора под боковыми полюсами, [Гн]. Для расчета ИП в соответствии с полученной функцией преобразования (1) необходимо определить потоки Ф1 и Ф2, проходящие через боковые полюса магнитопровода и наводящие в сигнальных катушках ЭДС. В соответствии с первым законом Кирхгофа можно записать: 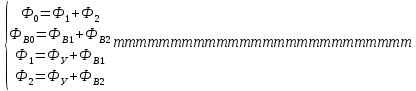 (3) (3)К этим четырем уравнениям необходимо добавить еще три (по количеству неизвестных), выбрав три независимых контура. Например,  (4) (4)Если пренебречь потоками утечки, так как, расстояние между стержнями полюсов статора существенно (в десятки раз) превышает величины зазоров между ротором и статором, и основываясь на выражениях для магнитных проводимостей можно утверждать, что проводимость утечки будет на 3-4 порядка ниже проводимости зазора, то можно считать, что весь магнитный поток проходит через воздушные зазоры между статором и ротором, то в схеме с сердечником ИП (рисунок 2) магнитные потоки 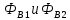 совпадают с потоками совпадают с потоками 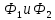 в самих полюсах магнитопровода и они соответственно равны: в самих полюсах магнитопровода и они соответственно равны: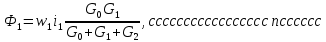 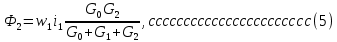 Найденные таким образом потоки используем для нахождения функции преобразования : 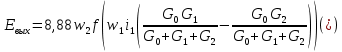 2.2 Расчет магнитных проводимостей. Рассчитаем магнитную проводимость воздушных зазоров методом разбивки на простые геометрические фигуры, в соответствии с методическим пособием [4]. Магнитная проводимость 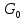 воздушного зазора. воздушного зазора.Магнитная проводимость этого зазора постоянна. Схема разбивки зазора на отдельные проводимости, когда ротор перекрывает весь статор:  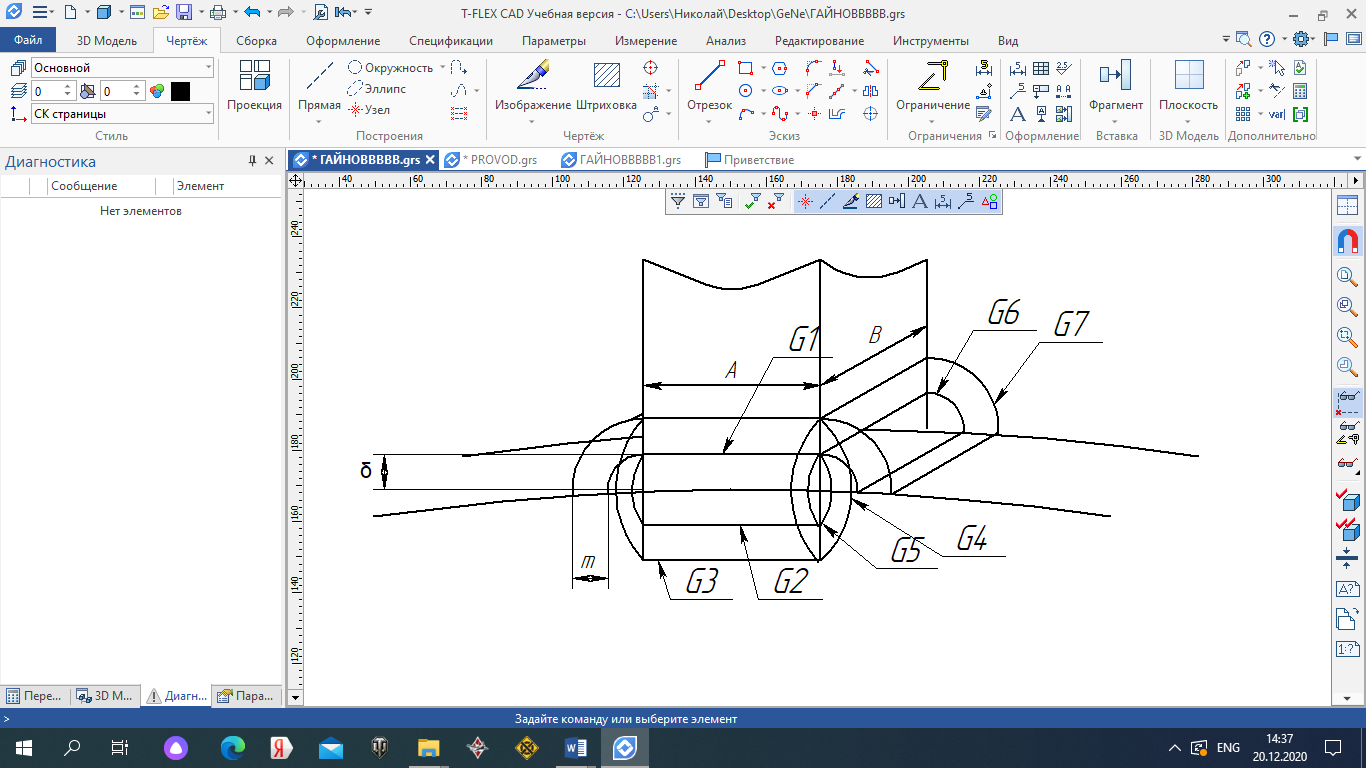 Рисунок 3 - Распределение магнитных силовых трубок воздушного зазора. Проводимость воздушного зазора 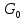 складывается из проводимостей складывается из проводимостей 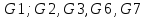 (по 2 геометрических фигуры каждой), (по 2 геометрических фигуры каждой),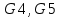 (по 4 геометрических фигуры каждой) (по 4 геометрических фигуры каждой)Геометрические параметры: 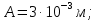 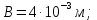 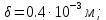 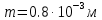 -некоторая произвольная величина, выбираемая по опытным данным и равная (1…2) -некоторая произвольная величина, выбираемая по опытным данным и равная (1…2)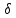 . .Проводимость воздушного зазора 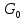 , Гн определяется следующим образом: , Гн определяется следующим образом: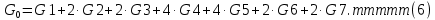 Проведем расчет проводимостей простейший геометрических фигур для воздушного зазора 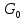 : :Прямоугольная призма:  Рисунок 4 - Распределение магнитной проводимости формы: прямоугольная призма. 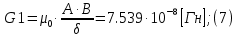 ½ кругового цилиндра: 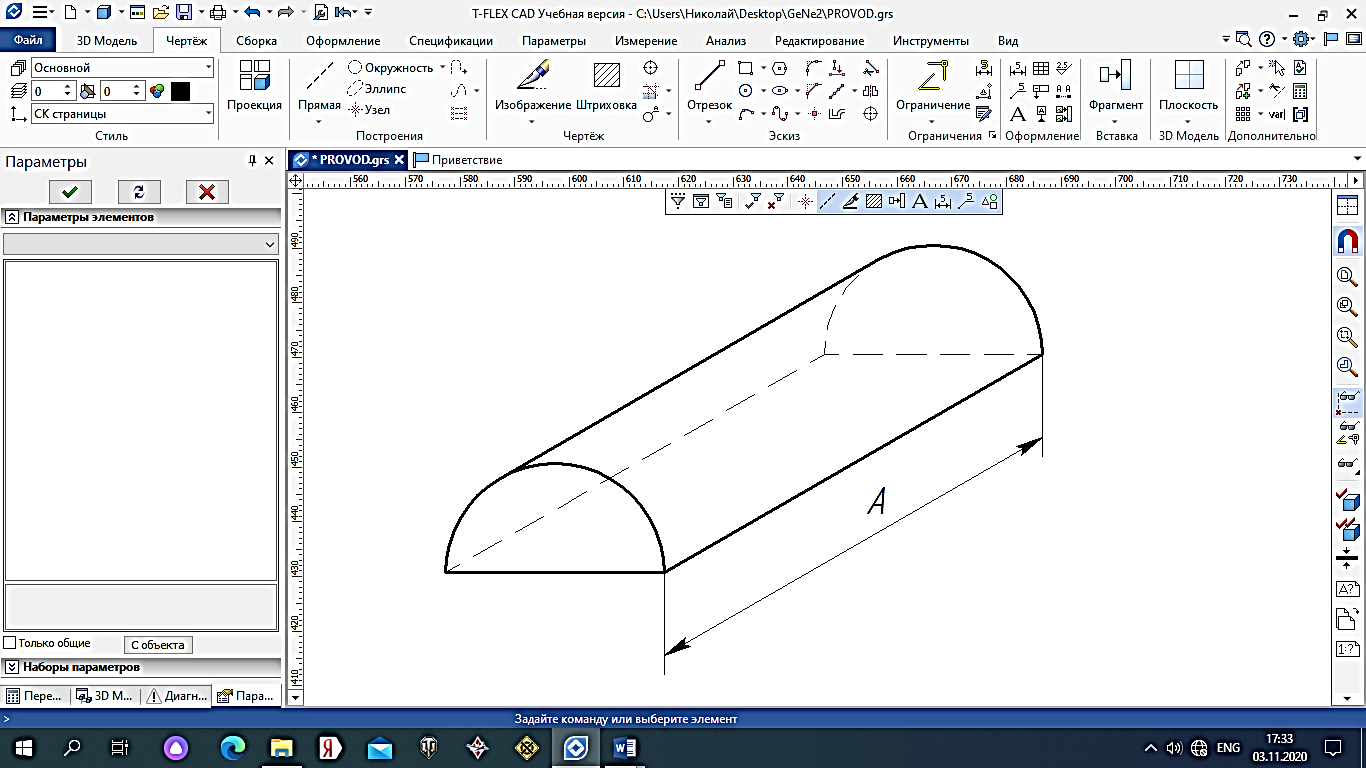 Рисунок 5 - Распределение магнитной проводимости формы: ½ кругового цилиндра. 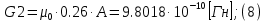 ½ кругового полого цилиндра: 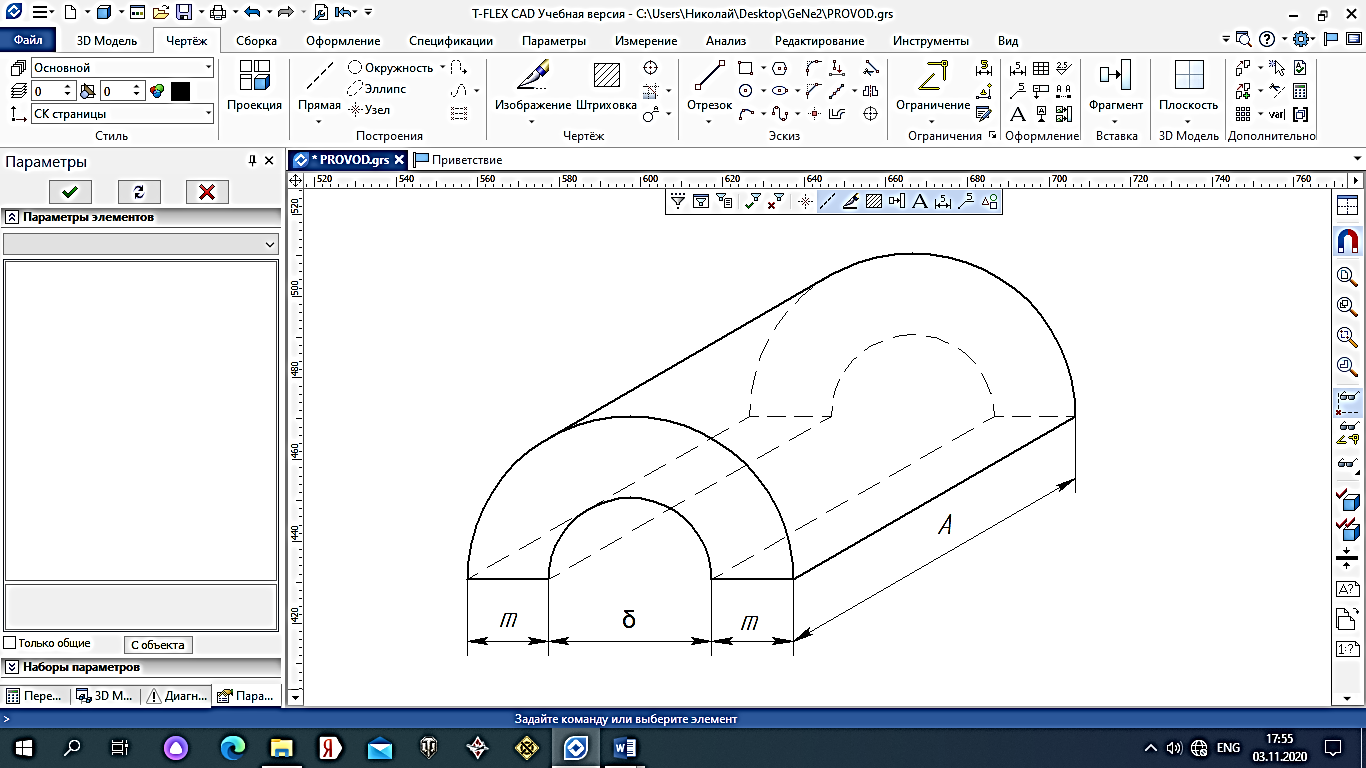 Рисунок 6 - Распределение магнитной проводимости формы: ½ кругового полого цилиндра. 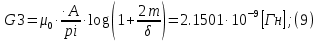 Шаровой квадрант: 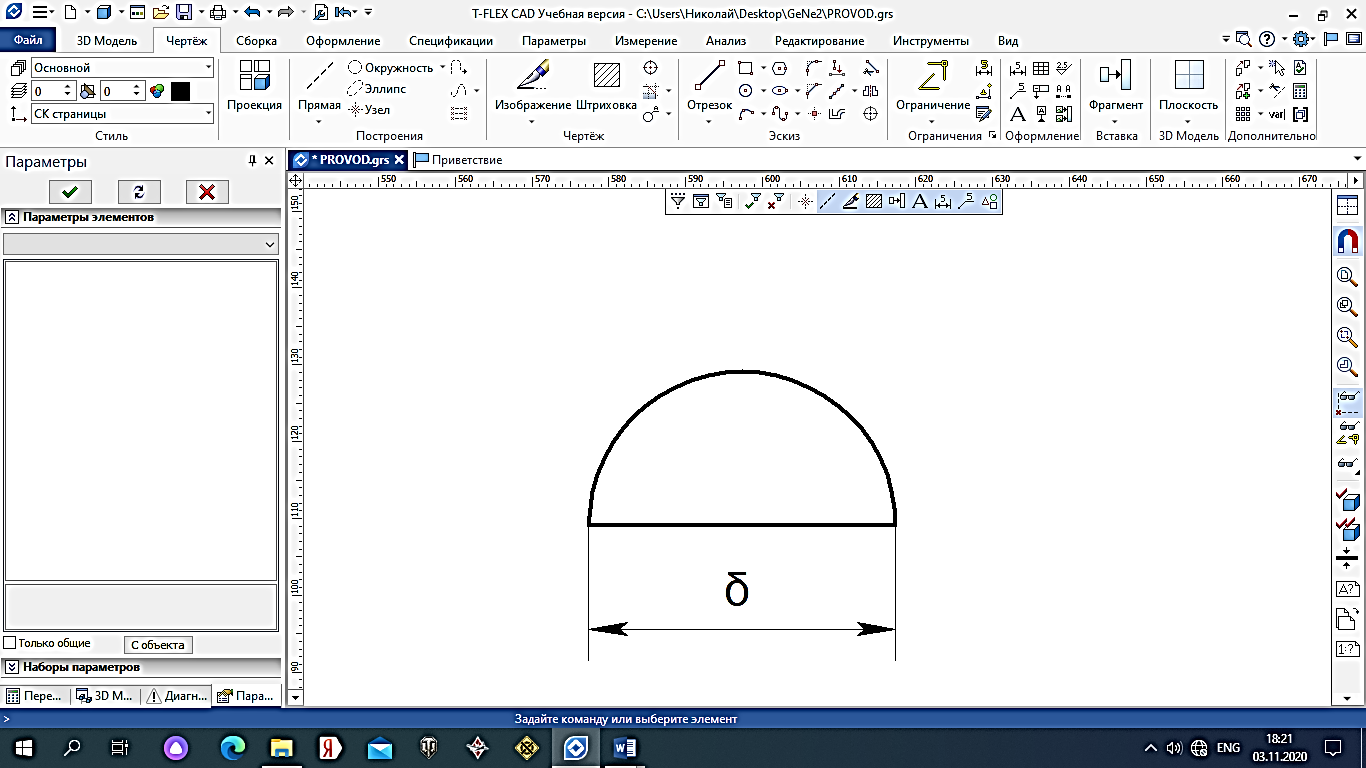 Рисунок 7 - Распределение магнитной проводимости формы: шаровой квадрант. 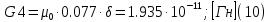 Квадрант шаровой оболочки: 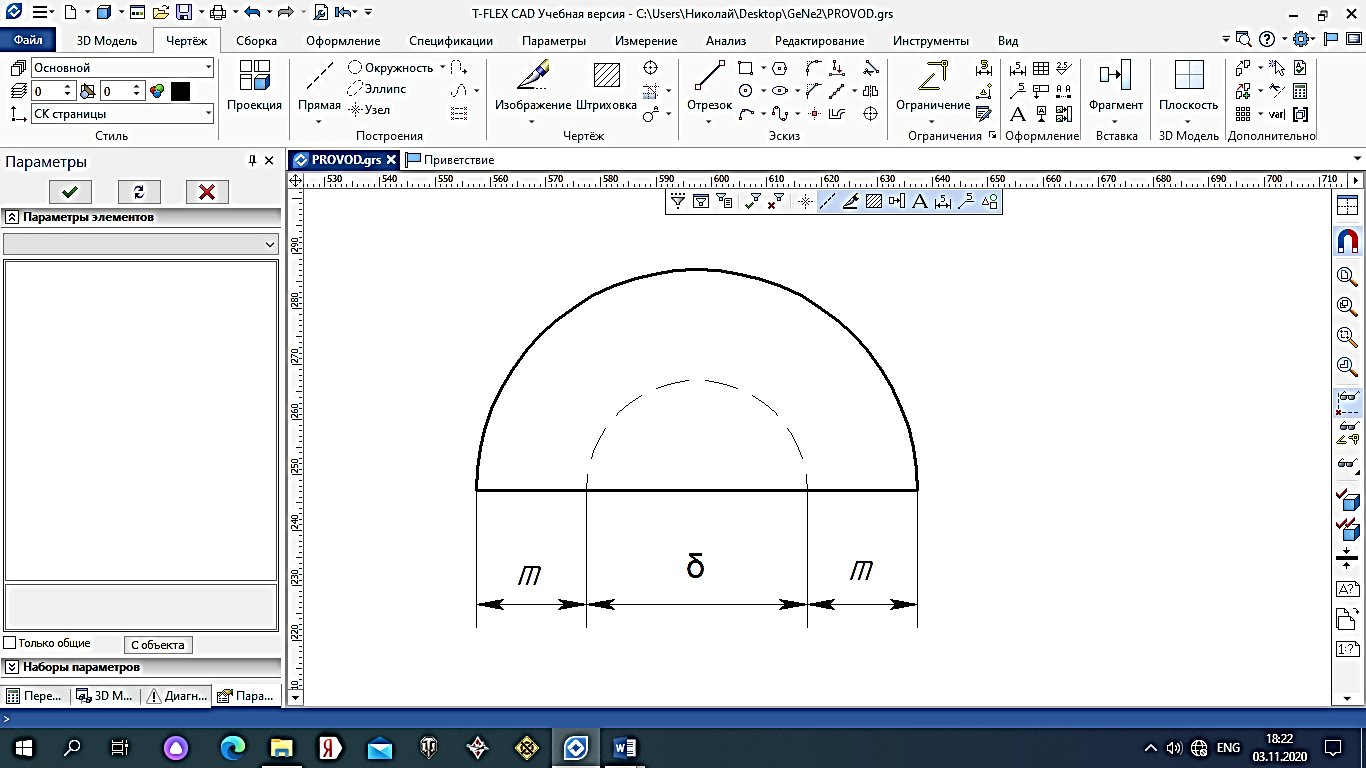 Рисунок 8 - Распределение магнитной проводимости формы: квадрант шаровой оболочки. 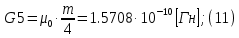 ¼ кругового кругового цилиндра: 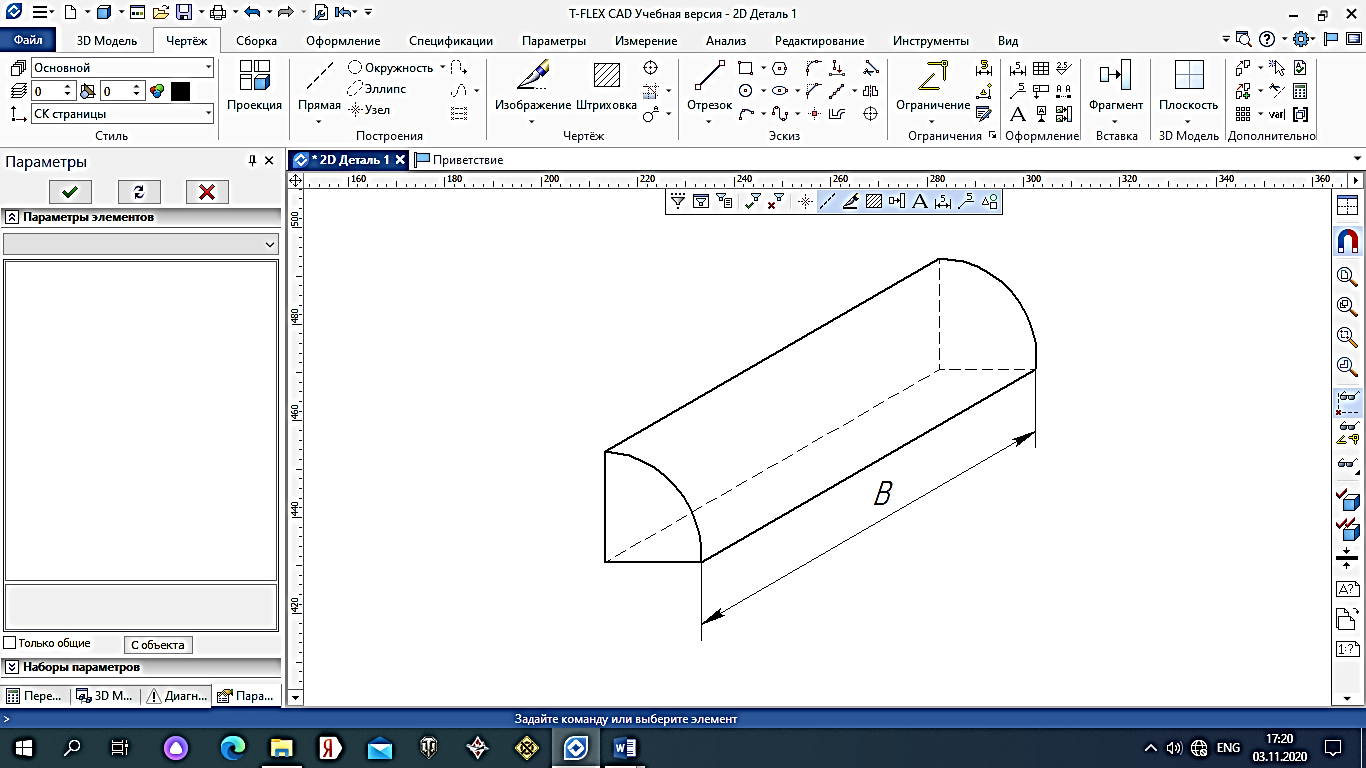 Рисунок 9 - Распределение магнитной проводимости формы: ¼ кругового кругового цилиндра. 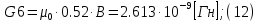 ¼ кругового полого цилиндра: 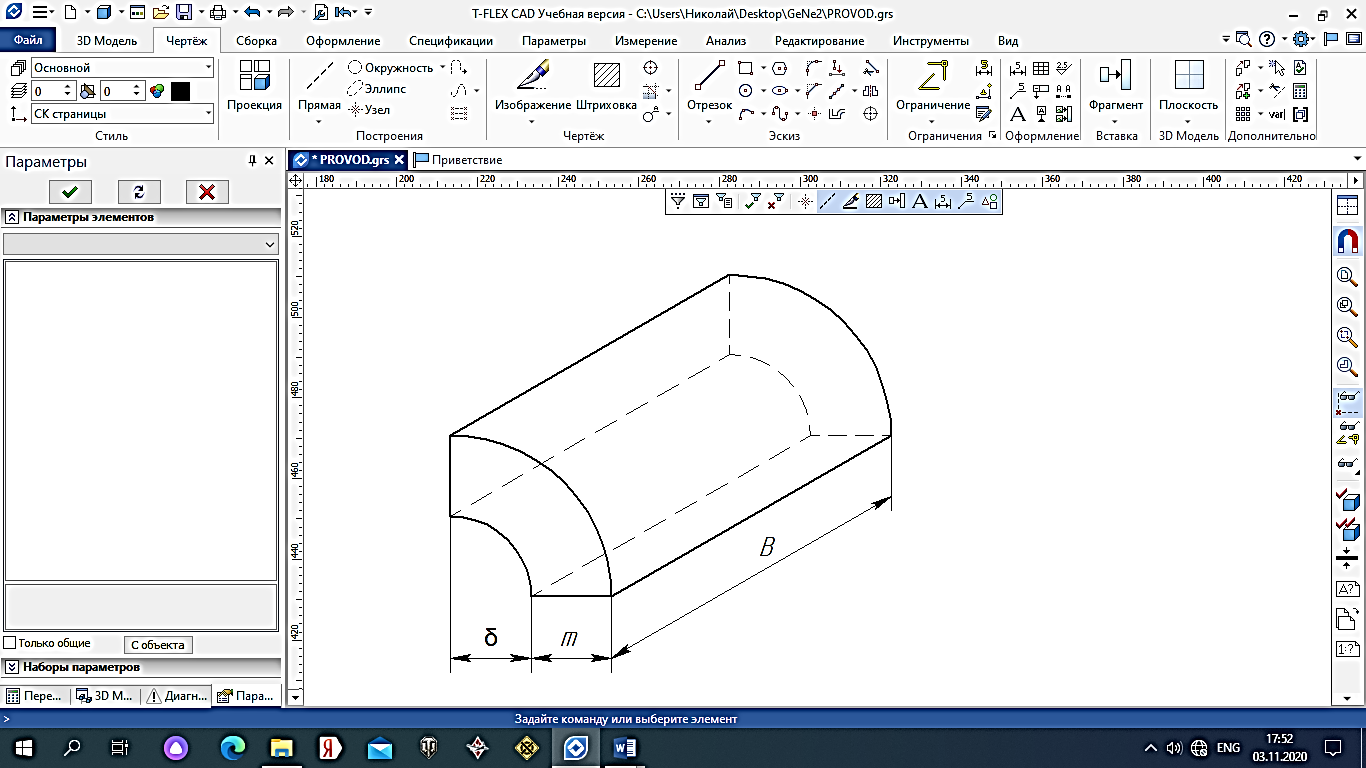 Рисунок 10 - Распределение магнитной проводимости формы: ¼ кругового кругового цилиндра. 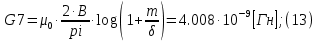 Подставим все найденные значения проводимостей в (27) и найдём суммарную проводимость зазора: 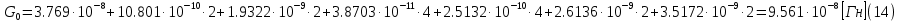 Магнитная проводимость 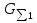 , , 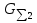 воздушных зазоров воздушных зазоров Магнитная проводимость данных зазоров изменяется при отклонения ротора на угол 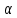 . .Схема разбивки зазора на отдельные проводимости, когда ротор перекрывает ½ статора. 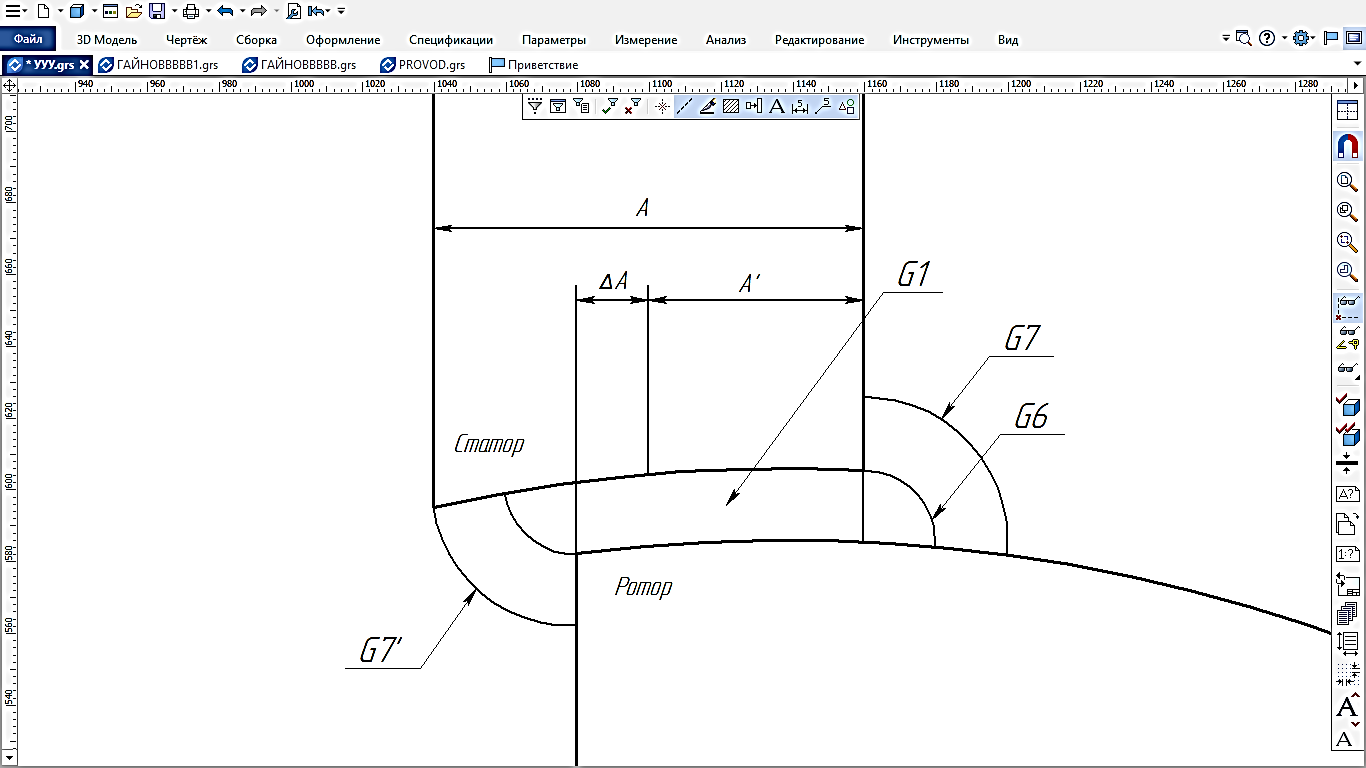 Рисунок 11 - Распределение магнитных силовых трубок воздушного зазора Геометрический размер перекрытия плоскостей стрежня статора и ротора изменяется при повороте ротора на значение: ∆Amax 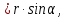 где где 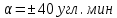 - - . .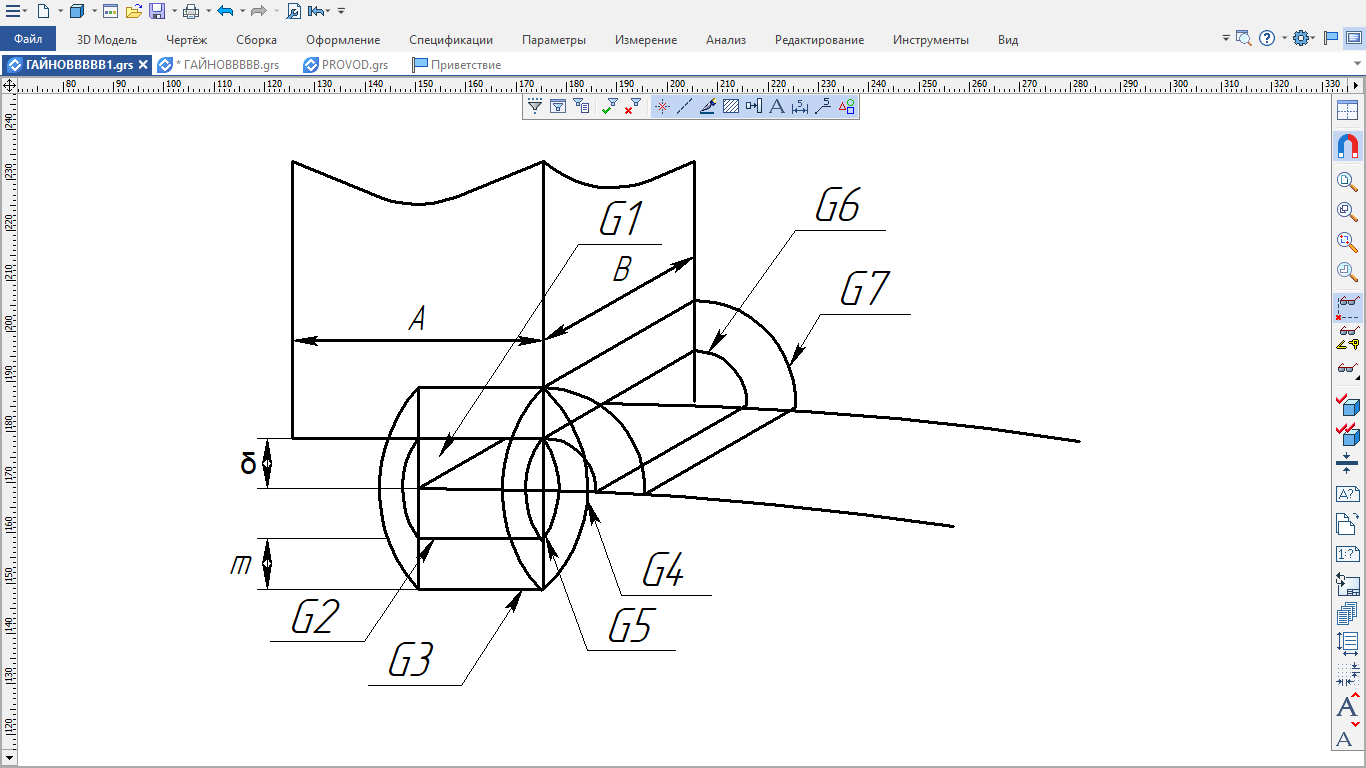 Рисунок 12 - Распределение магнитных силовых трубок воздушного зазора Проводимость воздушного зазора 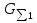 складывается из проводимостей складывается из проводимостей 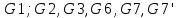 , ,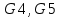 . .Геометрические параметры: 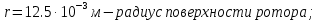 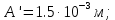 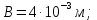 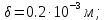 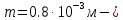 некоторая произвольная величина, выбираемая по опытным данным и равная (1…2) некоторая произвольная величина, выбираемая по опытным данным и равная (1…2)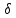 ; ;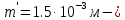 величина определяющая расстояние от крайней кромки ротора до края стержня. величина определяющая расстояние от крайней кромки ротора до края стержня.Проводимость воздушного зазора 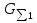 , Гн определяется следующим образом: , Гн определяется следующим образом: 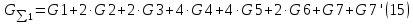 Суммарная проводимость воздушного зазора 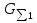 при отклонении ротора на определенный угол при отклонении ротора на определенный угол 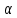 может определяться как: может определяться как: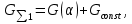 где 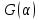 – проводимости фигур зависящие от угла – проводимости фигур зависящие от угла 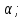 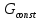 - проводимости фигур не зависящие от угла - проводимости фигур не зависящие от угла 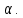 Проводимости фигур 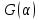 зависящие от угла зависящие от угла 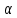 определяются в соответствии с рисунками 3,4 по формулам: определяются в соответствии с рисунками 3,4 по формулам: 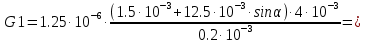 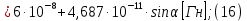 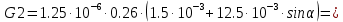 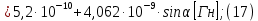 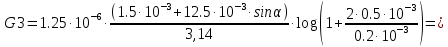 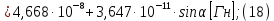 Проводимости фигур 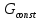 не зависящие от угла не зависящие от угла 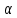 определяются в соответствии с рисунками 3,4 по формулам: определяются в соответствии с рисунками 3,4 по формулам: 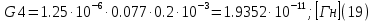 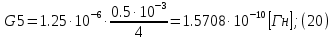 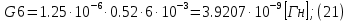 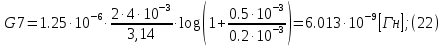 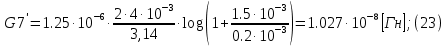 Таким образом, суммарная проводимость воздушного зазора 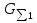 при отклонении ротора на угол при отклонении ротора на угол 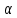 с учетом ранее полученных выражений будет описываться уравнением: с учетом ранее полученных выражений будет описываться уравнением: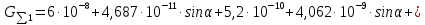 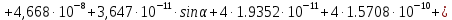 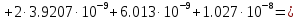 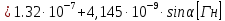 Проводимость воздушного зазора 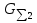 , определяется по аналогии с проводимостью , определяется по аналогии с проводимостью 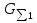 , с учетом отклонения ротора в противоположную сторону ∆A , с учетом отклонения ротора в противоположную сторону ∆A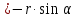 . .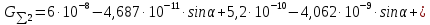 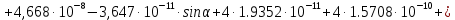 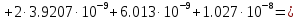 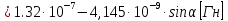 Подставим полученные выражения в формулу (*), в результате чего получим зависимость выходного ЭДС от угла α, описываемое уравнением: 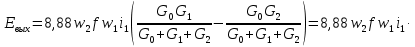 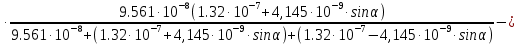 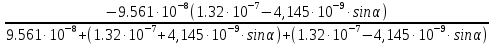 2.3 Расчет параметров катушки возбуждения 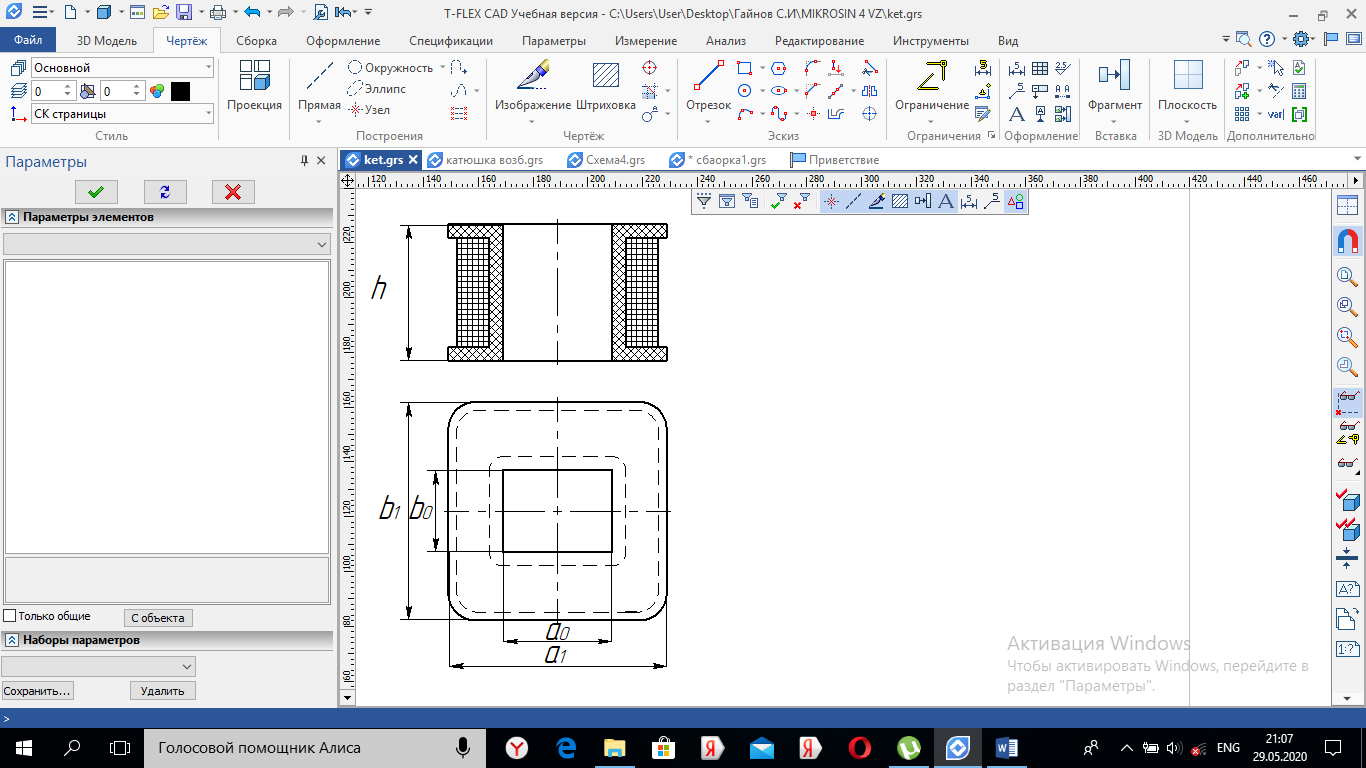 Рисунок 13 - Эскиз катушки возбуждения Геометрические размеры катушки в соответствии с конструктивными параметрами (см. рисунок 13): 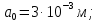 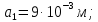 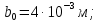 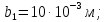 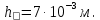 Расчет параметров катушки проводится в соответствии с методическим указанием [4]. Для расчёта числа витков катушки воспользуемся следующей формулой: 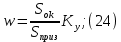 где 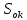 - площадь окна намоточного провода, - площадь окна намоточного провода, 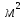 , ,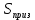 - площадь сечения намоточного провода с изоляцией, - площадь сечения намоточного провода с изоляцией, 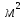 , ,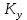 - коэффициент укладки провода ( - коэффициент укладки провода (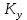 =0.6); =0.6);Площадь окна катушки намоточного провода равна: 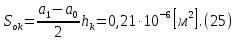 Площадь сечения намоточного провода с изоляцией равна: 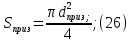 где 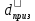 – диаметр намоточного провода с изоляцией, – диаметр намоточного провода с изоляцией,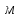 . .Плотность тока можно расписать следующим образом: 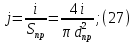 где 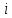 - сила тока, протекающего в катушке, А; - сила тока, протекающего в катушке, А; 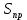 - площадь сечения намоточного провода без изоляции, - площадь сечения намоточного провода без изоляции,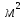 В свою очередь площадь сечения намоточного провода без изоляции равна: 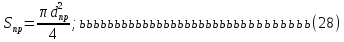 где 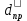 – диаметр намоточного провода катушки возбуждения без изоляции, – диаметр намоточного провода катушки возбуждения без изоляции, 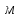 . .Активное сопротивление катушки определяется следующим образом: 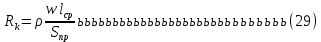 где 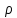 - удельное сопротивление материала намоточного провода. - удельное сопротивление материала намоточного провода.Для меди 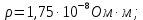 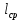 – средняя длина одного витка, м, определяется исходя из геометрических параметров катушки: – средняя длина одного витка, м, определяется исходя из геометрических параметров катушки: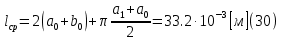 Сила тока i в катушке рассчитывается в соответствии с электрической схемой включения, по формуле: 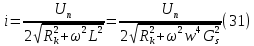 где 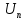 -напряжение питания, В; -напряжение питания, В; 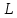 - индуктивность катушек возбуждения; - индуктивность катушек возбуждения; 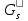 - суммарная проводимость при нулевом отклонении ротора, [Гн]. - суммарная проводимость при нулевом отклонении ротора, [Гн].В соответствии со схемой замещения (см. рисунок 3) суммарная проводимость при нулевом положении ротора: 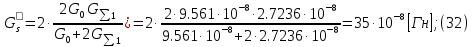 На первом этапе расчёта, в соответствии с методическим указанием [4] будем считать, что 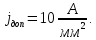 Определив предварительно магнитные проводимости при нулевом положении ротора, необходимые для расчета тока в катушках, и выполнив последовательно подстановку (28) и (30) в (29), (31) и далее в (27), с учетом (24), (25), (26), получим выражение, содержащее два неизвестных: диаметр намоточного провода без изоляции 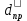 и диаметр намоточного провода с изоляцией и диаметр намоточного провода с изоляцией 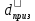 . На первом этапе расчета будем считать, что диаметр провода с изоляцией и без изоляции равны: . На первом этапе расчета будем считать, что диаметр провода с изоляцией и без изоляции равны: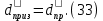 При таком допущении полученное выражение с двумя неизвестными преобразуется в уравнение с одним неизвестным параметром-диаметром намоточного провода. После определения по ГОСТ 26615-85 выбирается ближайший провод, к рассчитанному. При сделанном допущении следует учитывать условие 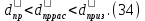 Проведем вывод формулы, в соответствии с алгоритмом приведенным. Подставим (28) в (29), после чего в формулу (31): 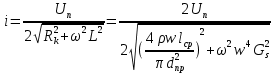 Полученное выражение подставим в формулу (27): 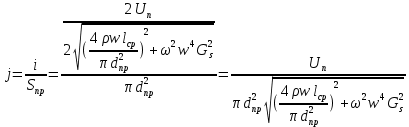 Проведем ряд преобразований и упрощений: 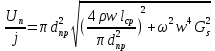 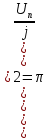 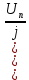 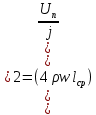 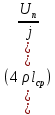 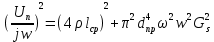 С учетом (24) полученное выражение примет вид: 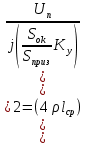 С учетом (26) полученное выражение примет вид: 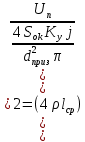 Проведем ряд преобразований и упрощений: 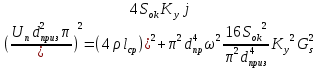 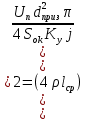 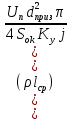 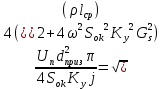 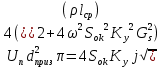 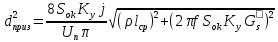 С учетом проведенного ряда преобразований и упрощений формула диаметра примет вид: 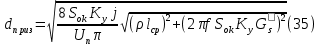 С учетом численных значений диаметр будет равен: 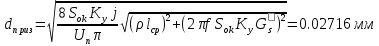 Для определения диаметров по условию (46), воспользуемся ГОСТом 26615-85: 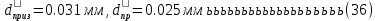 При выбранном диаметре намоточного провода производится окончательный расчёт числа витков (37), активного сопротивления катушки (40), плотности тока (42). Таким образом, число витков равно: 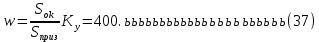 Площадь сечения провода с изоляцией равна: 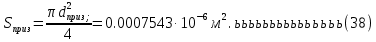 Площадь сечения провода без изоляции равна: 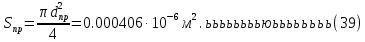 Активное сопротивление равно: 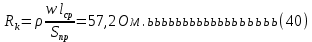 Сила тока равна: 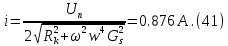 Плотность тока в катушке равна: 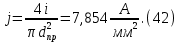 2.4 Расчёт параметров сигнальной катушки  Рисунок 14 - Эскиз сигнальной катушки Геометрические размеры катушки в соответствии с конструктивными параметрами (см. рисунок 14): 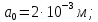 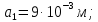 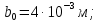 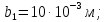 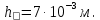 Диаметр провода примем из соображений конструктивной идентичности катушек возбуждения и сигнальной: 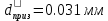 ; ;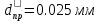 . .Рассчитаем параметры сигнальной катушки: 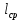 – средняя длина одного витка (м), определяется исходя из геометрических параметров катушки: – средняя длина одного витка (м), определяется исходя из геометрических параметров катушки: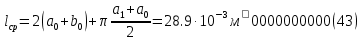 Площадь окна катушки намоточного провода равна: 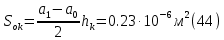 Площадь сечения провода с изоляцией равна: 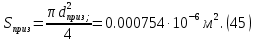 Площадь сечения провода без изоляции равна: 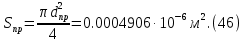 Таким образом, число витков равно: 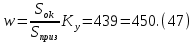 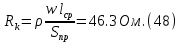 2.5 Расчет функции преобразования Рассмотрим движение ротора относительно статора на угол α. Зависимость выходного ЭДС от угла α описывается уравнением: 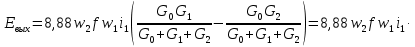 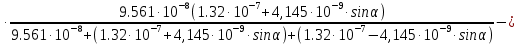 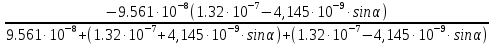 Подставим углы и произведем расчет зависимости выходного 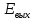 от угла α. Результаты расчета приведены в таблице 1. от угла α. Результаты расчета приведены в таблице 1.
Таблица 1 - Зависимость 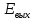 от перемещения ротора от перемещения ротораEвых,В 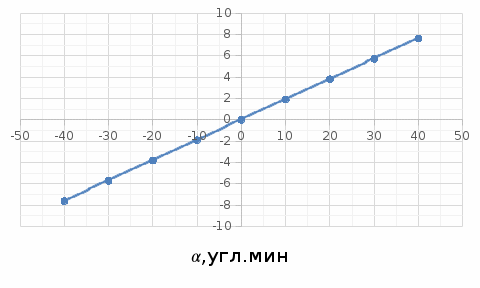 Рисунок 15 - График зависимости выходного ЭДС от угла 𝛼. Средняя крутизна характеристики определяется по формуле: 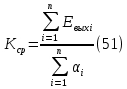 где 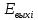 - значение выходного напряжения, В - значение выходного напряжения, В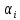 - значение угла рабочих перемещений, угл.мин. - значение угла рабочих перемещений, угл.мин.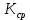 должна удовлетворять требуемой крутизне характеристики (не менее 35 мВ/угл.мин). должна удовлетворять требуемой крутизне характеристики (не менее 35 мВ/угл.мин). Итак, 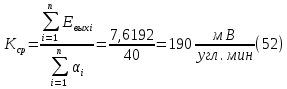 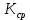 соответствует требованиям заданным параметрам. соответствует требованиям заданным параметрам.Расчёт погрешности линейности определяется по формуле: 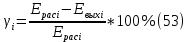 где 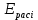 - расчетное значение линейной характеристики. - расчетное значение линейной характеристики.Расчетное значение линейной характеристики выходного ЭДС определяется: 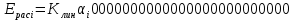 (54) (54)где 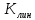 - коэффициент линейной характеристики, мВ/угл.мин. - коэффициент линейной характеристики, мВ/угл.мин.Результаты расчетов приведены в таблице 2.
Таблица 2 - Зависимость погрешности линейности от угла , % 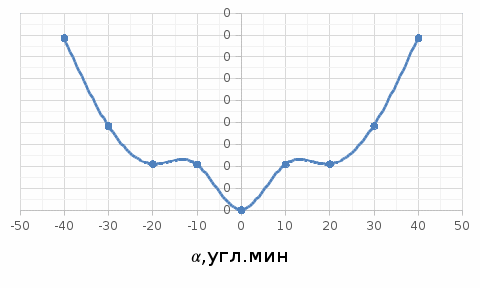 Рисунок 16 – График зависимости погрешности линейности от угла. Таким образом, максимальная погрешность равна: 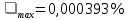 . . |

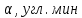
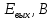
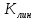 ,мВ/угл.мин
,мВ/угл.мин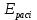 ,В
,В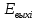 ,В
,В