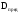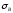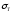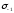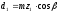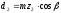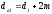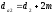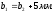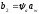курсовая. 2 расчет. 2. расчет зубчатой передачи редуктора. Выбор материала для колеса и шестерни
 Скачать 138.14 Kb. Скачать 138.14 Kb.
|
 2. РАСЧЕТ ЗУБЧАТОЙ ПЕРЕДАЧИ РЕДУКТОРА. 2.1. Выбор материала для колеса и шестерни. Колесо Материал колеса выбирается в зависимости от передаваемой мощности по ([I], табл. 3.1), а механические свойства материала по ([I], табл. 3.2), перевод твердости НВ в твердость HRC по ([I], рис. 3.1). Колесо: Сталь 45; Нормализация. Шестерня Материал шестерни выбирается аналогично колесу и той же марки, но термообработку берем улучшение т.к. зубья шестерни входят в зацепление чаще зубьев колеса. Шестерня: сталь 45; Улучшение. 2.1.1. Допускаемые контактные напряжения при расчетах на прочность определяется отдельно для шестерни и колеса. 2.1.1.1. Определяем коэффициент долговечности для зубьев шестерни и колеса: 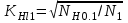 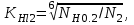 где NH0 – число циклов перемены напряжений, со-ответствующее переделу выносливости, согласно ([I], табл. 3.3), определяется в зависимости от средней твердости поверхности зубьев: Шестерня: 262 НВ, тогда NH01= 25 млн. циклов Колесо: 207 НВ, тогда NН02=16,5 млн. циклов. 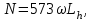 N – число циклов нагружения зубьев колеса и шестерни за весь срок службы; 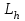 – рабочий ресурс привода: – рабочий ресурс привода: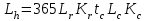 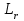 – срок службы привода (по условию); – срок службы привода (по условию);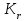 – коэффициент годового использования, (Кr = 1); – коэффициент годового использования, (Кr = 1);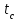 – продолжительность смены, (8 часов); – продолжительность смены, (8 часов);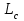 – число смен (Lc = 3); – число смен (Lc = 3);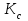 – коэффициент сменного использования (Kc = 0.85) – коэффициент сменного использования (Kc = 0.85)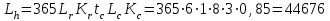 час. час.Р  абочий ресурс привода принимаем: 40000 час. абочий ресурс привода принимаем: 40000 час.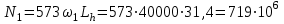 циклов. циклов.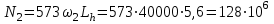 циклов. циклов.тогда: 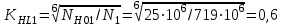 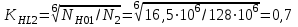 Согласно ([I], стр. 55), 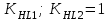 . .2.1.1.2. По формулам ([I], табл. 3.1), определяем допускаемые контактные напряжения для колеса и шестерни. 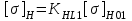  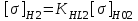 где 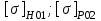 – допускаемые напряжения при числе циклов переменных напряжений определяются для конических передач с прямыми зубьями из условия: – допускаемые напряжения при числе циклов переменных напряжений определяются для конических передач с прямыми зубьями из условия: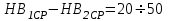 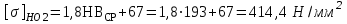 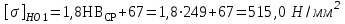 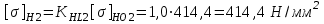 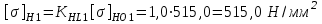 Расчет передачи ведут по меньшему значению. 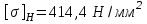 2.1.2. Допускаемые напряжения изгиба. 2.1.2.1. Определяем коэффициент долговечности для зубьев шестерни и колеса: 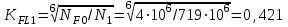 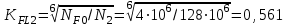 NF0 – число циклов перемены напряжений для всех сталей, соответствующее пределу выносливости, согласно ([I], стр. 56), принимаем: 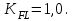 2.1.2.2. По формуле ([I], табл. 3.1), определяем допускаемое напряжение изгиба для колеса и шестерни. 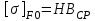 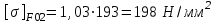 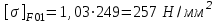 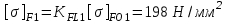 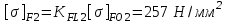 Т  аблица 3. аблица 3.
2.2 Проектный расчет. 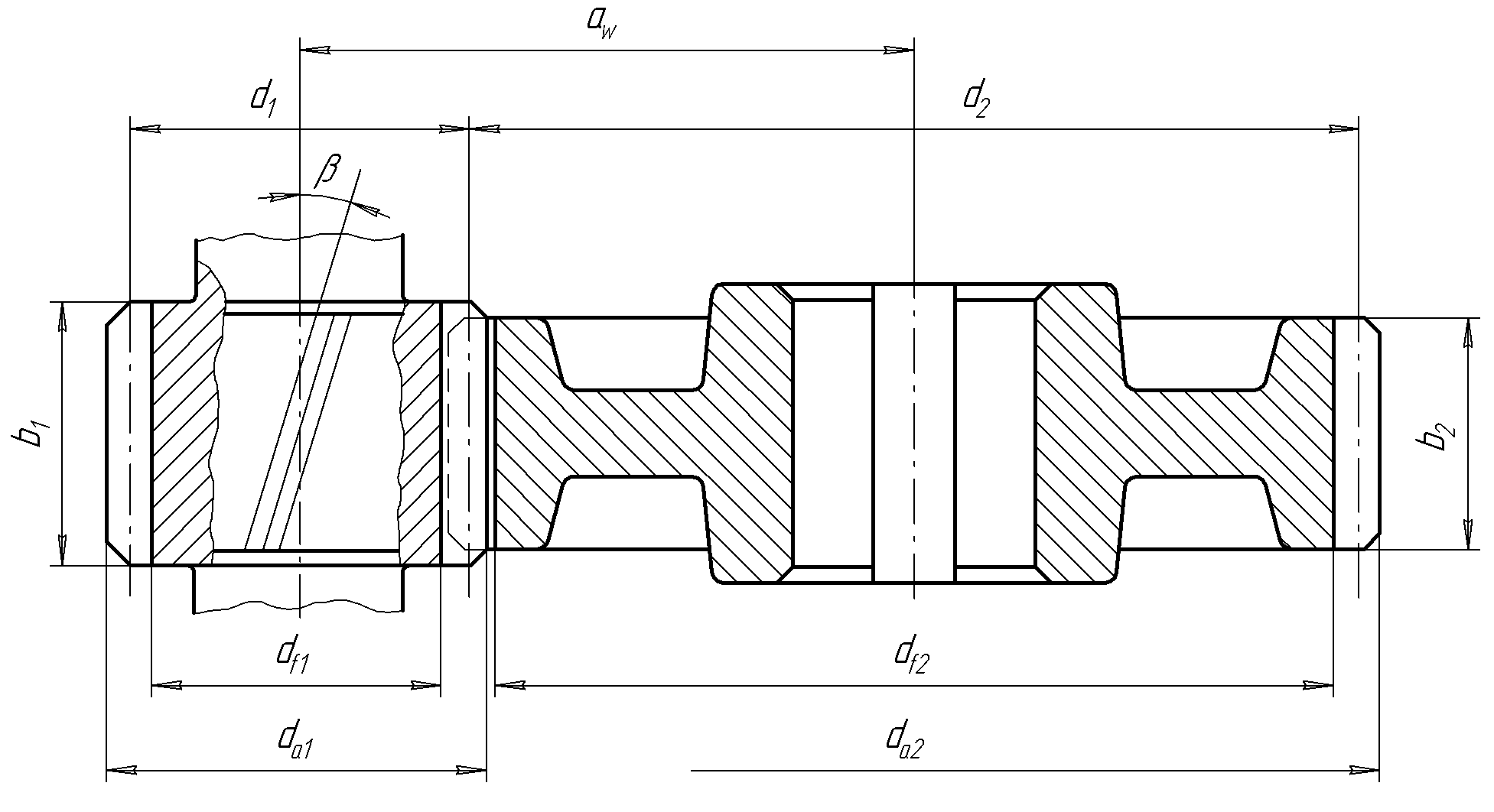 Рис 1. Геометрические параметры цилиндрической зубчатой передачи. 2.2.1 Определяем межосевое расстояние. 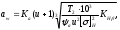 где 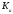 – вспомогательный коэффициент, принимаем: – вспомогательный коэффициент, принимаем: 43 для косозубых передач. 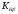 – коэффициент, учитывающий распределения нагруз- – коэффициент, учитывающий распределения нагруз- ки по ширине венца, принимаем 1,0. 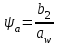 – коэффициент ширины венца колеса, принимаем 0,3 для симметричного расположения шестерни. – коэффициент ширины венца колеса, принимаем 0,3 для симметричного расположения шестерни.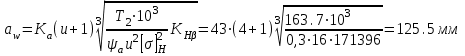 Полученное значение округляем по ГОСТ 6636-69 принимаем: 125 мм. 2  .2.2. Определяем модуль зацепления, мм. .2.2. Определяем модуль зацепления, мм.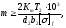 где 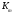 – вспомогательный коэффициент, принимаем: 5,8 для косозубых колес. – вспомогательный коэффициент, принимаем: 5,8 для косозубых колес.Д 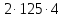 елительный диаметр колеса, мм. 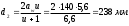 =200 мм 5 . Ширина венца колеса, мм. 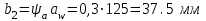 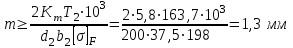 Полученное значение округляем по ГОСТ 6636-69, принимаем 1,5 мм. 2.2.3. Определяем угол наклона зубьев, 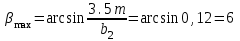 градуса. градуса.Принимаем угол наклона зубьев: 6 градусов. 2.2.4. Определяем суммарное число зубьев шестерни и колеса: 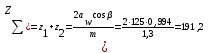 Принимаем: 191. 2.2.5. Уточняем угол наклона зубьев, 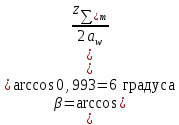 2.2.6. Определяем число зубьев шестерни. 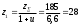 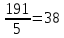 2 191-38=153 .2.7. Определяем число зубьев колеса. 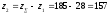 2.2.8. Определяем фактическое передаточное число и проверяем отклонения от заданного. 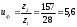 153/38=4,02 2.2.9. Определяем фактическое межосевое расстояние. 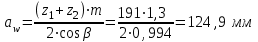 . .2.2.10. Определяем основные геометрические параметры шестерни и колеса: Т  аблица 4. аблица 4.
2.3. Проверочный расчет 2.3.1. Проверка зубьев по контактным напряжениям. 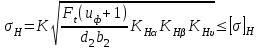 где F1 – окружная сила в зацеплении, Н. 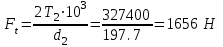 . .K– вспомогательный коэффициент, для косозубых передач: K = 376. 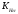 – коэффициент, учитывающий распределения нагрузки между зубьями, принимаем по ([I], рис. 4.2) в зависимости от окружной скорости колеса, 1,1. – коэффициент, учитывающий распределения нагрузки между зубьями, принимаем по ([I], рис. 4.2) в зависимости от окружной скорости колеса, 1,1.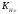 – коэффициент динамической нагрузки, определяется по ([I], табл. 4.3) в зависимости от окружной скорости колеса, – коэффициент динамической нагрузки, определяется по ([I], табл. 4.3) в зависимости от окружной скорости колеса,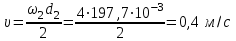 . .и степени точности передачи, определяется по ([I], табл. 4.3) принимаем 9-ю степень точности, тогда: 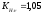 . .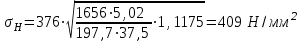 . .Условие контактной прочности выполняется. 2.3.2. Проверяем напряжения изгиба зубьев шестерни и колеса. Колесо: 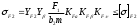 Ш  естерня: естерня: 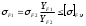 где 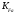 – коэффициент, учитывающий распределение нагрузки между зубьями, принимаем по ([I], стр. 66) в зависимости от окружной скорости шестерни и степени точности, принимаем: – коэффициент, учитывающий распределение нагрузки между зубьями, принимаем по ([I], стр. 66) в зависимости от окружной скорости шестерни и степени точности, принимаем: 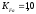 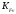 – коэффициент динамической нагрузки определяется аналогично, принимаем по ([I], стр. 66) – коэффициент динамической нагрузки определяется аналогично, принимаем по ([I], стр. 66) 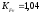 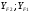 – коэффициенты формы зуба шестерни и колеса, определяются в зависимости от эквивалентного числа зубьев шестерни и колеса, определяется по ([I], табл.4.4) интерполирование в зависимости от эквивалентного числа зубьев шестерни и колеса. – коэффициенты формы зуба шестерни и колеса, определяются в зависимости от эквивалентного числа зубьев шестерни и колеса, определяется по ([I], табл.4.4) интерполирование в зависимости от эквивалентного числа зубьев шестерни и колеса.Интерполируя значения ([I]табл. 4.4): 3,7 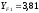 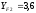 = 3,6 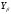 – коэффициент учитывающий наклон зуба, принимаем: – коэффициент учитывающий наклон зуба, принимаем: 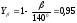 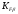 – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев колес принимаем: – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев колес принимаем: 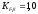 Колесо: 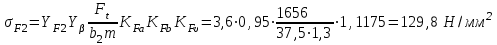 Условие выполняется. Шестерня: 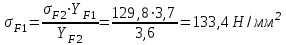 условие выполняется. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||