РГР по Оптимизации1.xlsx. Расчет распределение нагрузки между агрегатами тэц
 Скачать 186.19 Kb.
|
|
Некоммерческое акционерное общество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ ИМЕНИ ГУМАРБЕКА ДАУКЕЕВА» Кафедра «Тепловые энергетические установки» РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №1,2 Вариант-1 По дисциплине: «Оптимизационные задачи в теплоэнергетике» На тему: «Расчет распределение нагрузки между агрегатами ТЭЦ» Специальность: 7М07102-Теплоэнергетика Выполнил: Әбубәкір Мөлдір Группа: МТЭ(ТЭС)н-20-2 Приняла: проф. каф. ТЭУ Кибарин А.А. _______________________ «___» _______________ 20__г. (оценка) (подпись) Алматы 2021 Цель работы: Составить модель и алгоритм расчета распределения нагрузки между агрегатами ТЭЦ. Задание: На базе представленной модели рассчитать и заполнить матрицу коэффициентов. Для решения системы линейных алгебраических уравнений использовать симплекс-метод. Таблица 1
1 Описание стандартной программы решения задачи линейного программирования симплекс-методом Программа определяет экстремум функции Z=  при ограничениях вида: 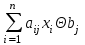 ; xj 0 ; bj 0 ; I=1,m; = «», «=», «»где  -заданные вещественные числа; хj –искомые переменные. Ввод Рисунок 1-Блок-схема Описание параметров: А- входной двухмерный массив (матрица) размерности МхN1, где М=m, N1 =n+1, состоящий из элементов aij (и столбцов) и дополнительно нулевого столбца с номером N1. В массив размерности М, содержащий элемент bi, при выходе b содержит значения искомых неизвестных; с–массив размерности МхN1, первые n элементов которого содержат значения сj , остальные элементы равны нулю, b-массив размерности М, содержащий признаки типов ограничений: Nb(i)  При выходе в Nb –индексы неизвестных по возрастанию, значения которых расположены в соответствующей последовательности в массиве b. Остальные неизвестные, индексы которых перечислены в массиве Nb, равны нулю, Nj- массив размерности N1 содержит следующие значения: Nj(j)=-j, если ожидается (на основе оценки), что в решение войдет хj0, Nj(j)=j - во всех остальных случаях j=1, N1; М-число ограничений, М=m; N1-число неизвестных, увеличенное на единицу, т.е. N1 = n+1; EPS-относительная погрешность вычислений (10-6); z – результирующее значений функции, если получено оптимальное решение. IER-входной параметр, IER0 задача на максимум, IER0, задача на минимум. При выходе IER=1–функция не ограничена, IER=-1 несовместимость условий (не все искусственные переменные выведены из базиса). 2 Основные теоретические положения решения задач оптимизации при распределении нагрузки на турбоагрегаты ТЭС Одним из эффективных способов повышения экономичности использования оборудования тепловых станций является оптимальное ведение работы агрегатов, установленных на станции. Для теплоэлектроцентралей особенно характерна установка разнотипного оборудования с различными экономическими показателями. Поэтому вопрос о распределении нагрузки между турбоагрегатами, вырабатывающими электрическую и тепловую нагрузку особенно актуален. Постановка задачи поиска оптимального распределения нагрузки между работающими агрегатами базируется на рассмотрении зависимостей расходов топлива на работающие агрегаты станции, от многочисленных факторов: Вi = ( Q ni , Q тi ,N эi, Р тi) , (2.1) где Вi – расход топлива на i-й агрегат станции; Q ni , Q тi – расход тепла на промышленный и теплофикационные отборы пара i-го агрегата; Nэi–электрическая мощность, вырабатываемая i-м агрегатом; Р тi – давление теплофикационного отбора i-го агрегата. Суммарный расход топлива на станции Вст определяется как: Вст =  , (2.2)где n – число агрегатов на станции. Оптимальному распределению нагрузки между агрегатами соответствуют такие значения Q ni, Q тi, Nэi , при известных величинах Q nст, Qтст, при которых значение Вст имеет минимальное значение и обеспечиваются заданные значения производственной Qnст и отопительной Qтст тепловых нагрузок станции. Таким образом, математическая постановка задачи сводится к минимизации целевой функции вида: Вст = min (2.3)При ограничениях:  = Q пст = Q тст или 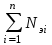 = N эст (2.4)Qni min Qni Qni max Q ti min Qti Qti max Nэi min Nэi Nэi max В самом общем случае эта задача является задачей нелинейного программирования и ее решение возможно при известных функциях или алгоритме расчета расхода топлива для работающих агрегатов. Функции вида (1.1) называются энергетическими характеристиками агрегатов. 3 Составление математической модели Рассмотрим задачу на примере работы турбины Т-100/120-130. Объект представляет собой станцию, схема которой представлена на рисунке 1.1. Таким образом, в качестве объекта исследования принимается станция с заданным составом оборудования.  Рисунок 2 Энергетическая характеристика турбины, установленной на станции выписываем из таблицы 1.1. Q=10,5Pт+2N-1,13Nт +Qт NT=0,635(Qт -13) / Pт0,1 , со встроенным пучком NT=0,7(Qт1 -30) / Pт0,14 , Qт1 = Qт+Qпучка Поскольку Qн р ,ка ,тр - величины постоянные, минимизировать можно расходы тепла на станции Qст = Qi , поэтому целевая функция для рассматриваемой задачи будет иметь вид: Q=10,5Pт+2N-1,13*(0,635(Qт -13) / Pт0,1) +Qт Преобразуя данное выражение, получим: Y= 2N+(-0,717/ (Pт0,1)+1)* Qт+10,5Pт+9,32/ (Pт0,1) (1.14) Запишем систему ограничений: Qт =Qт ст Qт Qтмin Qт Qтмах N Nмin N Nмах Вводим обозначения: N–Х1, Qт–Х2, С1=2; С2=-0,717/(Pт)0,1+1; Qх=10,5* Pт+9,32/(Pп2)0,1; Получим математическую модель задачи линейного программирования: Y=C1*Х1+ C2*Х2
В последней постановке минимизируется величина Y, а не Q ст в данном случае, это не влияет на результат, поскольку в левой части уравнения суммируется постоянная величина. Система ограничений записана в удобной для представления матрице ограничений и для использования выбранного алгоритма. В качестве алгоритма принимаем симплекс-метод, который может быть реализован с помощью стандартной программы. Блок-схема алгоритма решения представлена на рисунке 1. При выборе значений, с использованием 4, правых частей для ограничений полагаем Nмin=85МВт, Nмах=110МВт,Qтмах=184МВт, Qтмin=57, Qт ст=150 МВт. |