инвестиции Пензенский институт. инвест в 25 пенза. 2. Расчетная часть 5

• Название: 2. Расчетная часть 5
• Анкор: инвестиции Пензенский институт
• Дата: 07.08.2022
• Размер: 430.77 Kb.
• Имя файла: инвест в 25 пенза.docx
• Тип: Документы; #641951
• страница: 1 из 3

СОДЕРЖАНИЕ

1.Понятие фактора времени. Методы учета фактора времени в инвестиционных расчетах. Экономический смысл приведения разновременных затрат и результатов к одному моменту времени 2

2. Расчетная часть 5

Список использованной литературы 22

1. Понятие фактора времени. Методы учета фактора времени в инвестиционных расчетах. Экономический смысл приведения разновременных затрат и результатов к одному моменту времени

Инвестиционный процесс носит долговременный характер, в результате чего между началом этапа вложения капитальных затрат по проекту и началом этапа получения учетной прибыли от него (возврата инвестиций) проходит достаточно большой период времени. Длительность этого периода зависит от формы протекания инвестиционного процесса. Существуют три основных формы протекания инвестиционного процесса: последовательная, параллельная и интервальная. При параллельном протекании инвестиционного процесса формирование инвестиционной прибыли начинается обычно еще до полного завершения процесса инвестирования капитала. При последовательном протекании процесса инвестиционная прибыль формируется сразу после окончания инвестирования средств в проект. В случае интервального протекания инвестиционного процесса между периодом завершения инвестирования капитала и формированием инвестиционной прибыли проходит определенный период времени.

Следовательно, между вложением средств в инвестицию, полным возвратом этих средств и получением инвестиционной прибыли проходит значительный промежуток времени. Т.е. движение номинальных потоков денежных средств инвестиции осуществляется с значительным лагом времени, а следовательно такие потоки должны быть приведены в сопоставимый вид по фактору времени. Для этого необходимо осуществить корректировку размеров номинальных денежных потоков инвестиции с целью получения текущей (сегодняшней) их оценки. Текущая оценка предполагаемых поступлений зависит от двух факторов:

От времени поступления таких потоков.

От альтернативной стоимости не использования денежных средств в обороте, т.е. от размера текущей ставки процентного дохода по депозитным банковским вкладам.

С точки зрения движения финансовых потоков, инвестиционный процесс ассоциируется с накоплением средств на депозитном счету по сложному проценту. Т.е. такая схема депозита, когда основной вклад и проценты, регулярно по нему начисляемые, не изымаются (не используются) собственником продолжительный период времени (более 1 года). Основные операции (функции), осуществляемые с использованием сложного процента накопления сопоставимы с элементарными инвестиционными операциями и используются при проведении базовых инвестиционных расчетов. Функции сложного процента изучаются в разделе финансовой математики.

Функциями сложного процента, используемыми в базовых инвестиционных расчетах, являются:

Накопление денежной единицы (единичного вклада) S

Текущая стоимость денежной единицы ν

Текущая стоимость аннуитета α

Взнос на амортизацию денежной единицы РМТ

Будущая стоимость аннуитета Sα (накопление периодической денежной единицы)

Фактор фонда возмещения SFF.

Текущая стоимость денежной единицы ν показывает сегодняшний эквивалент стоимости денежного вклада, который мы ожидаем к получению через t лет, если сегодняшняя ставка сложного процента і.

Процесс определения сегодняшнего (текущего) эквивалента будущего денежного потока также называют дисконтированием, а коэффициент приведения – коэффициентом дисконтирования

Формула коэффициента дисконтирования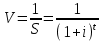

Взнос на амортизацию денежной единицы РМТ показывает размер регулярного периодического платежа, поступающего t лет на погашение кредита, приносящего процентный доход i. Из этого взноса погашается и основная сумма кредита и проценты за его использование.

Будущая стоимость аннуитета Sα позволяет узнать чему будет равна в конце ожидаемого периода t стоимость серии одинаковых взносов, депонированных под i процентов в конце каждого интервала поступления. Формула коэффициента будущей стоимости аннуитета: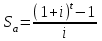



Фактор фонда возмещения SFF показывает, чему должен быть равен размер регулярного периодического платежа, поступающего t лет на сложный депозит под i процентов, с целью образования известной суммы к концу периода. Формула коэффициента фонда возмещения: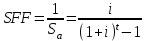



Все формулы финансовой математики представлены для случая, если начисления процентов и поступления на вклад осуществляются 1 раз в году. Если же частота накопления и начисления должна быть больше чем один раз в год, все формулы трансформируются одинаковым образом: ставка процента i делится на частоту накопления σ, а период накопления t, выраженный в годах, умножается на частоту накопления σ.