РАЗДЕЛ СК. 2. Расчетноконструктивный раздел 1 Расчет плиты междуэтажного перекрытия
 Скачать 3.39 Mb. Скачать 3.39 Mb.
|
 2. Расчетно-конструктивный раздел 2.1 Расчет плиты междуэтажного перекрытия В расчетно-конструктивной части дипломного проекта рассчитана и сконструирована плита междуэтажного перекрытия ПК60.15-8АтVт. 2.1.1 Конструктивная схема Плита укладывается на стену из газобетонных блоков по слою цементно-песчаного раствора. 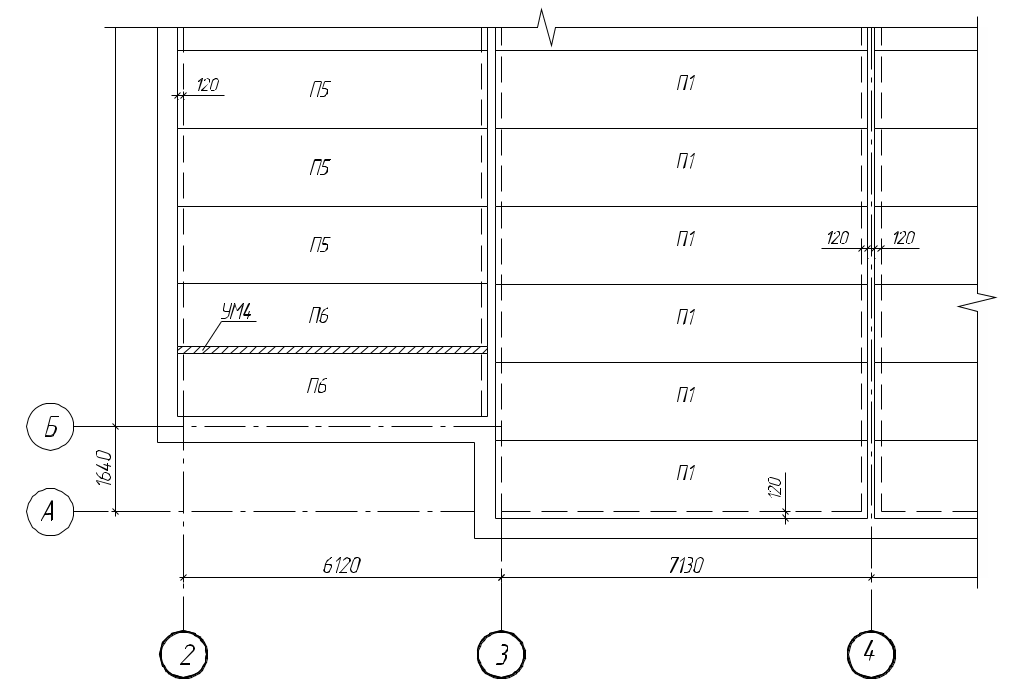 Рис. 2.1 Схема расположения плит перекрытия 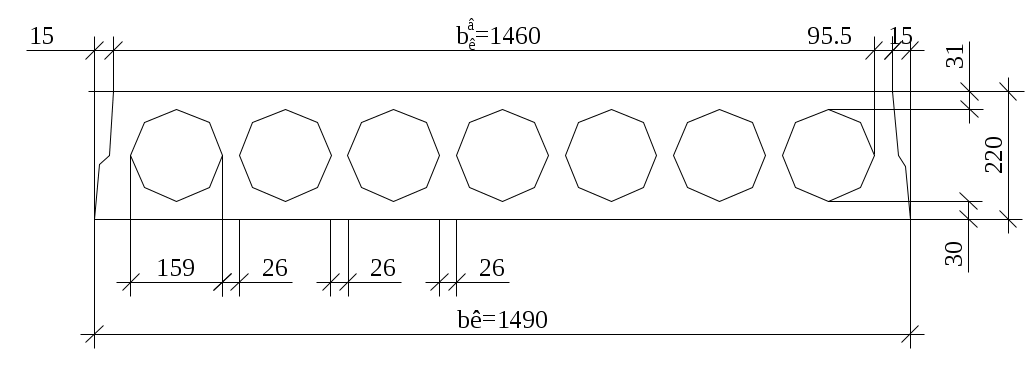 Рис.2.2. Поперечное сечение плиты перекрытия 2.1.2 Расчетная схема и нагрузки Расчетная схема плиты представляет собой статически определимую однопролетную балку, загруженную равномерно распределенной нагрузкой, в состав которой входят постоянная, включающая вес пола, собственный вес плиты, и временная.  Рис.2.3. Расчетная схема плиты перекрытия Нормативная нагрузка (кН/м²) от собственной массы плиты: где ρ = 2500 кг/м³ — плотность железобетона; Аполн — площадь поперечного сечения плиты по номинальным размерам, м²; Апуст — суммарная площадь пустот в пределах габарита сечения, м². Подсчёт нормативных и расчётных нагрузок с подразделением на длительно и кратковременно действующие выполняется в табличной форме. Таблица 2.1 Нормативные и расчётные нагрузки на плиту перекрытия
2.1.3 Статический расчёт Для выполнения расчётов по первой и второй группам предельных состояний нужно вычислить следующие усилия: Изгибающий момент (кН∙м) от полной расчётной нагрузки: Изгибающий момент (кН∙м) от полной нормативной нагрузки: Изгибающий момент (кН∙м) от нормативной длительно действующей нагрузки: Поперечная сила (кН) от полной расчётной нагрузки: где l0 – расчетный пролет, определение которого показано на рис. 2.3.
Подбор сечения  Рис.2.4. Расчетное сечение плиты Вычисляем размеры эквивалентного сечения. В расчете поперечное сечение пустотной плиты приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот равновеликими по площади квадратными со стороной h1. Высота полки: Приведенная толщина ребер: где Рабочая высота сечения: где Проверяем отношение 2.1.4 Характеристики прочности бетона и арматуры Плита перекрытия запроектирована из тяжелого бетона класса В25, подвергаемого тепловой обработке при атмосферном давлении. Продольная арматура класса Ат-800 с электротермическим натяжением на упоры форм. В зависимости от принятого класса бетона и арматуры определяются характеристики бетона и арматуры. Коэффициент условий работы бетона Начальный модуль упругости бетона Продольная арматура класса Ат-800 с электротермическим натяжением на упоры форм: 2.1.5 Определение начальных напряжений в арматуре Начальное напряжение в арматуре определяем из условия принятой передаточной прочности бетона: Предварительное напряжение арматуры: Проверяем выполнение условия: где Условие выполняется. Найдем предельное отклонение предварительного напряжения по формуле: Коэффициент точности натяжения: При проверке по образованию трещин в верхней зоне плиты обжатии принимаем: Предварительное напряжение с учетом точности натяжения: Окончательное предварительное натяжение арматуры с учетом минимального значения суммарных потерь 2.1.6 Расчет прочности плиты по сечению, нормальному к продольной оси Расчетное сечение представляет балку таврового сечения полкой в сжатой зоне. Проверяем условие [17, п. 3.19]: т.е. граница сжатой зоны проходит в полке и расчет производим как для прямоугольного сечения шириной b=b'f=1460мм. Граничная высота сжатой зоны [16, п. 3.1.2.3]: 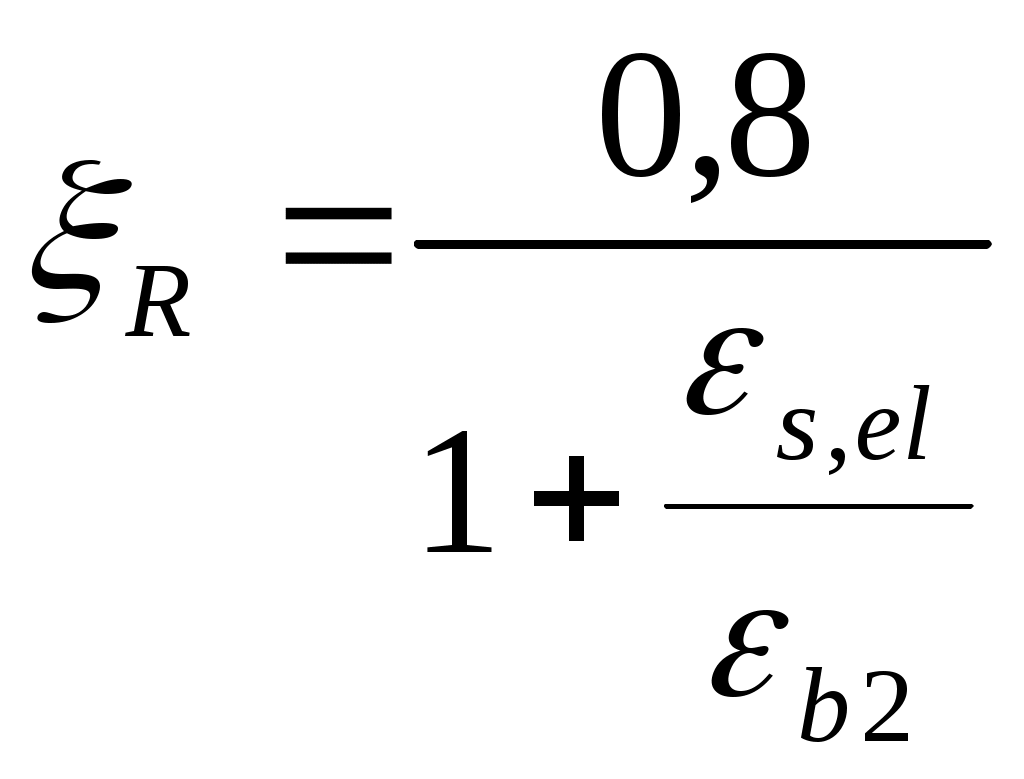 (2.18) (2.18)εb2 – предельная относительная деформация сжатого бетона, принимаемая равной 0,0035. 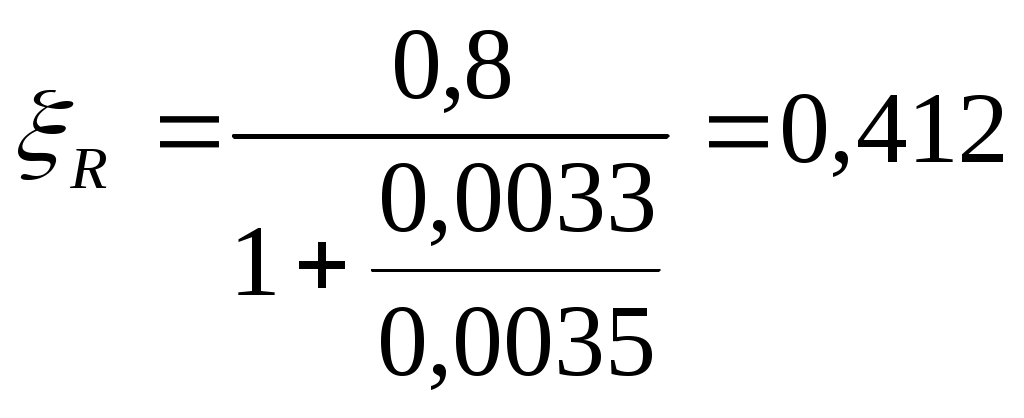 Т.к. Определяем площадь поперечного сечения рабочей предварительно напряженной арматуры [13, п. 3.14]: Принимаем 214 Ат-800 с площадью 2.1.7 Проверка прочности нормального сечения Высота сжатой зоны [16, ф. 36]: где Скорректируем а и h0: Рабочая высота панели: Несущая способность сечения [16, ф. 35]: Вывод: подобранное сечение удовлетворяет по несущей способности. 2.1.8 Расчет прочности плиты по сечению, наклонному к продольной оси Расчет предварительно напряженных элементов по бетонной полосе между наклонными сечениями производят из условия [16, п. 3.1.5.2]: φb1 - коэффициент, принимаемый равным 0,3. Условие выполняется, прочность бетонной полосы обеспечена. Расчет предварительно напряженных изгибаемых элементов по наклонному сечению производят из условия [16, п. 3.1.5.3]: где Qsw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении: где φb2- коэффициент, принимаемый равным 1,5. Условие выполнено, прочность наклонного сечения обеспечена. По расчёту поперечная арматура не требуется. В ребрах устанавливается конструктивно каркасы, продольные стержни которых состоят из арматуры Ø4, 3 В500, поперечные - из арматуры Ø 3 B500. Чтобы обеспечить прочность полок панели на местные нагрузки, в пределах пустот в нижней зоне сечения предусмотрена сетка С-2 в продольном направлении Ø5 В500 с шагом 300мм, в поперечном направлении - Ø4 В500 с шагом 70мм. В верхней зоне предусмотрена сетка С-1 в продольном направлении Ø3 В500 с шагом 300мм, в поперечном - Ø3 В500 с шагом 200мм. 2.1.9 Расчет монтажной петли Для монтажных петель применяется арматурная сталь класса A240. Диаметр петель назначается по требуемой площади поперечного сечения (см²) одной петли, определяемой при условии распределения веса плиты на три петли с учетом коэффициента динамичности 1,4 и коэффициента, учитывающего сгиб петли 1,5. где Rs=215MIIa - расчетное сопротивление арматуры класса A-I; qcвн=3,18 кН/м2 - нормативная нагрузка от собственного веса плиты; bк=1,49м - конструктивная ширина плиты; lпл = 5,58м - конструктивная длина плиты. Принимаем 4 петли Ø12 с Asфакт.= 1,131см² каждая, что больше As1=0,86см². 2.1.10 Определение геометрических характеристик приведенного сечения для расчета плиты по предельным состояниям второй группы. 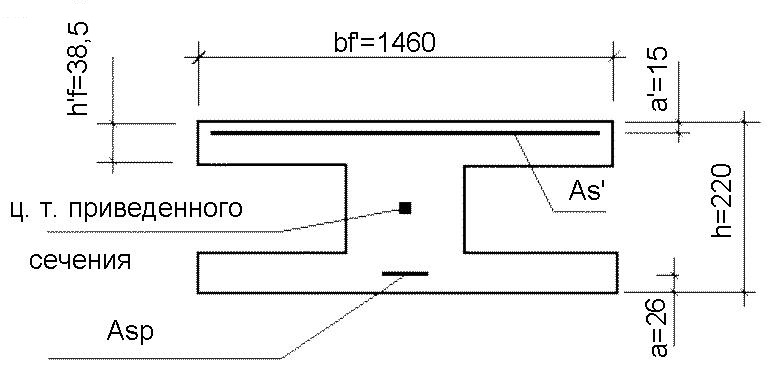 Рис.2.5. Геометрические характеристики сечения Определяем геометрические характеристики приведенного сечения: где Es= 200·103мПа – модуль упругости арматуры Eb= 30·103мПа – модуль упругости бетона класса В25 Площадь приведенного сечения: где где 0,568см² – площадь сечения продольной арматуры сеток С1 Статический момент относительно нижней грани сечения плиты: Расстояние от центра тяжести приведенного сечения до нижней грани плиты: Момент инерции приведенного сечения относительно центра тяжести: 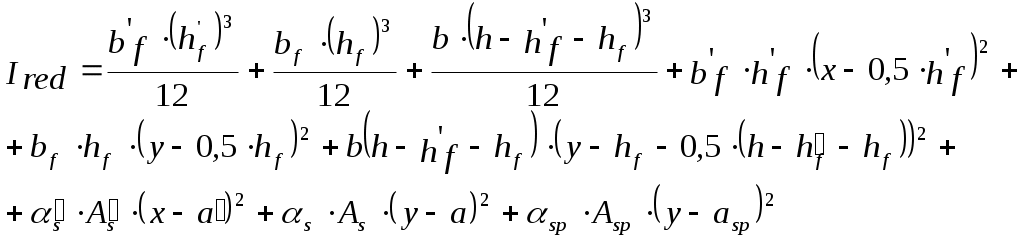 (2.28) (2.28)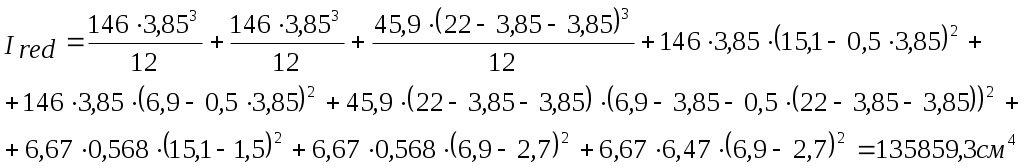 Момент сопротивления сечения для растянутой грани сечения: Расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести и тоже наименее удаленной от растянутой зоны [16, п. 4.2.2.5]: Упругопластический момент сопротивления по растянутой зоне: где 2.1.11 Потери предварительного напряжения арматуры Предварительное напряжение в арматуре без учета потерь принимаем [17, п. 2.26]: Определяем первые потери: – от релаксации напряжений в арматуре [16, п. 2.2.3.3]: – от температурного перепада σsp2=0, так как при пропаривании форма нагревается вместе с панелью; – потери от деформации формы σsp3 и анкеров σsp4 при электротермическом натяжении арматуры равны нулю. Усилие обжатия с учетом первых потерь: Сумма первых потерь: σsp(1) = σsp1 = 21,6МПа Эксцентриситеты усилия где Напряжение в бетоне при обжатии [16, п. 2.2.3.10]: Устанавливаем значение передаточной прочности бетона из условия [17, п.2.3]: Принимаем Определяем вторые потери напряжений – потери от усадки [16, п.2.2.3.7] где Вычисляем сжимающие напряжения в бетоне на уровне центра тяжести площади напрягаемой арматуры от усилия обжатия: – потери напряжений в рассматриваемой напрягаемой арматуреот ползучести бетона определяют по [16, п. 2.2.3.8]: 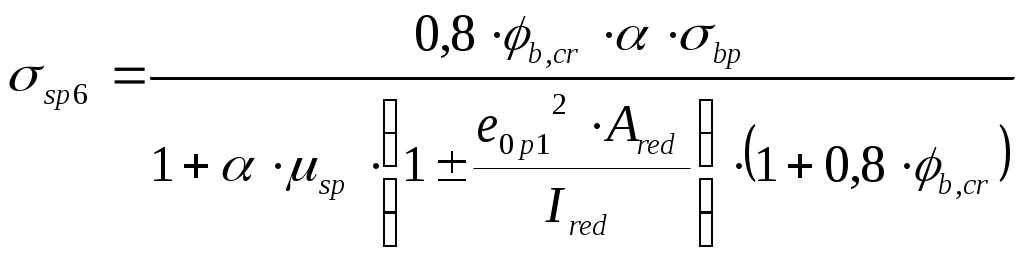 , (2.40) , (2.40) где φb,сr = 2,5 - коэффициент ползучести бетона по [16, табл. 5], μsp– коэффициент армирования, равный 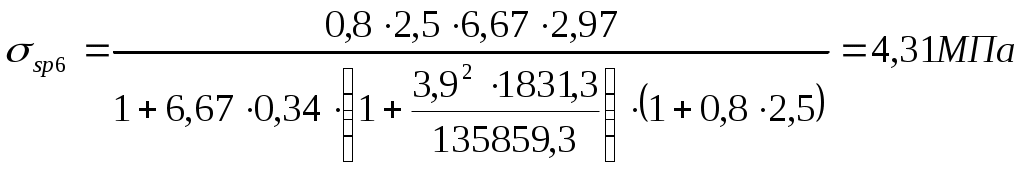 Вторые потери для арматуры: Суммарная величина потерь напряжения: Принимаем значение всех потерь Усилие обжатия с учетом всех потерь: 2.1.12 Оценка трещинообразования нижней зоны балки в стадии эксплуатации Расчет по образованию трещин производят на действие полных нормативных нагрузок. Расчет заключается в проверке условия: где Условие выполняется, следовательно, трещины образовываться не будут. 2.2 Расчет монолитного участка 2.2.1 Сбор действующих нагрузок Подсчёт нормативных и расчётных нагрузок на монолитный участок выполняется в табличной форме. Таблица 2.2 Нормативные и расчётные нагрузки на монолитный участок
Нагрузка от собственной массы монолитного участка: Определяем расчетную и нормативную нагрузки с учетом ширины монолитного участка. Определяем максимальный изгибающий момент от действия расчетных нагрузок: Максимальная поперечная сила на опоре от действия расчетных нагрузок: 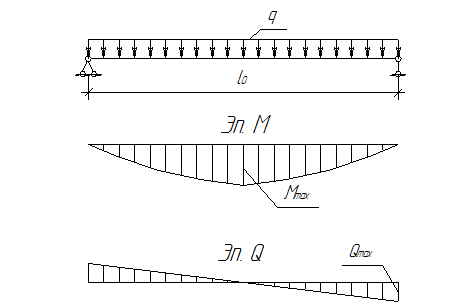 Рис. 2.6. Расчетная схема Для монолитных участков применяем легкий бетон класса В15, с расчетным сопротивлением Rb=8,5МПа. Армирование производим сетками с рабочей арматурой класса А400. Расчетное сопротивление арматуры Rs=355МПа. 2.2.2 Определение требуемого сечения арматуры Подбор продольной арматуры осуществляем по изгибающим моментам как для балки прямоугольного сечения с шириной b=40см и высотой h, равной принятой толщине плиты hпл. 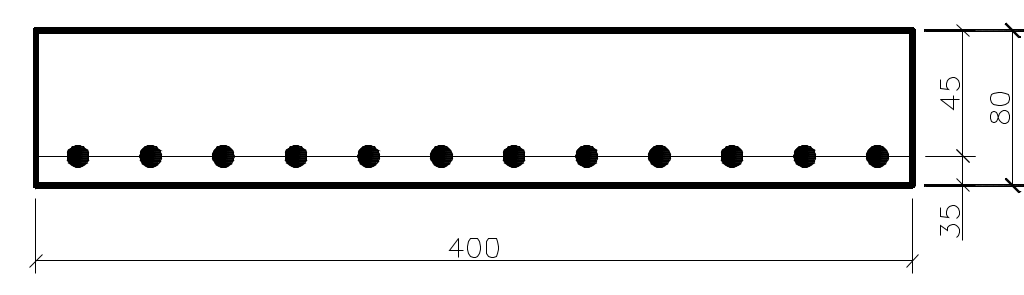 2.4. Расчетное сечение Рабочая высота монолитного участка, см, где a=1,5см– расстояние от центра тяжести арматуры до ближайшей грани сечения. Производим конструктивный расчет: Определяем параметр По полученному значению Определяем требуемую площадь рабочей арматуры, см2, для участка протяженностью 1м. По требуемой площади рабочей арматуры принимаем 5 стержней d8 класса AIII (As=2.52 ) с шагом 150мм на 1 м.п. монолитного участка УМ-5. 2.3. Расчет прочности по наклонным сечениям Необходимость расчета определяется условием: Где Q – поперечная сила от внешней расчетной нагрузки: Условие прочности выполняется, поперечная арматура устанавливается без расчета. В качестве распределительной арматуры принимаем принимаем AIII диаметром 8мм с шагом 200мм. 2.4. Проверка трещиностойкости Мr < Мcrc Мr = М- момент внешних сил относительно оси, проходящей через ядровую точку, наиболее удаленную от растянутой грани сечения Мcrc- момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин Мcrc=Rbt,crc ·Wpl ·100 +Мrp Мrp -момент усилия P относительно той же оси, что и для определения Мr . Где Р- предварительное усилие. еор- эксцентриситет приложения силы P относительно центратяжести приведенного сечения (см) 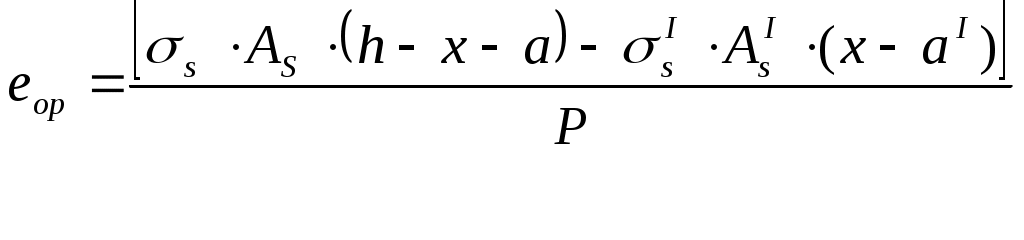 Для изгибаемых элементов без предварительного напряжения усилие Р рассматривают как внешнюю растягивающую силу. Усилие предварительного обжатия с учетом всех потерь: при 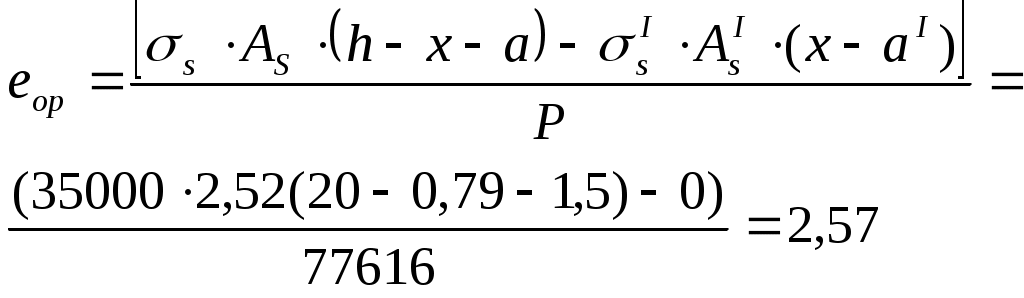 x- высота сжатой зоны. r- расстояние от центра тяжести приведенного сечения до верней ядровой точки. Где 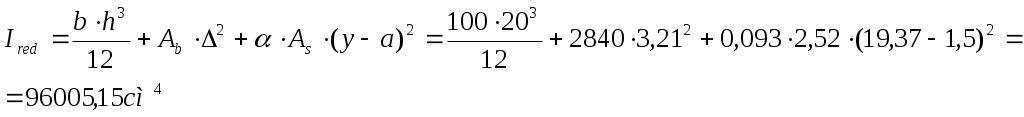 Момент сопротивления приведенного сечения с учетом неупругих деформаций бетона растянутой зоны Момент сопротивления приведенного сечения с учетом неупругих деформаций бетона растянутой зоны Мcrc=Rbt,crc ·Wpl ·100 +Мrp=1,4·7434,6·100 +323,07=104116,4 2.5. Проверка жесткости Прогиб панели k=5/48 для равномерно загруженной свободно опертой балки Величина кривизны 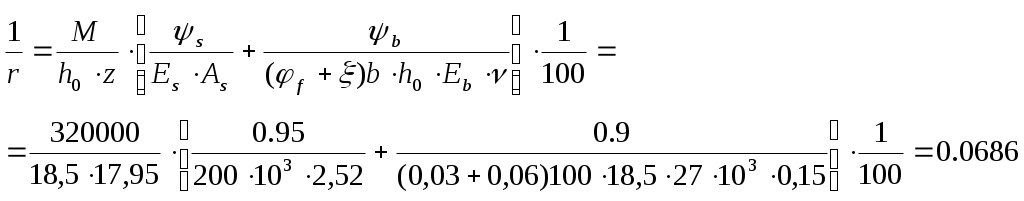 Здесь Плечо внутренней пары сил δ= M/(Rb, ser·b·h02 ·100)=32000/(18,5·103·100·18,52·100)=0,072 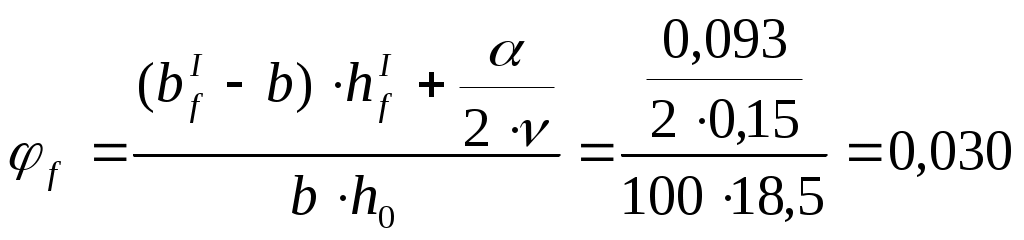 Относительная высота сжатой зоны бетона сечения с трещиной 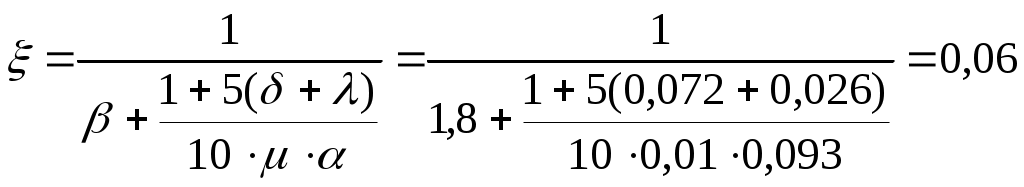 Следовательно, принятое сечение монолитного участка и армирование удовлетворяет требованиям расчета по I и II группам предельных состояний. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
