Сопромат. Р и собственного веса (78 кНм 2 ). Найти перемещение сечения ii (рис 1). Исходные данные F 20 см 2 а2,8 см b3,0 см с1,6 см Р1800 Н Рис 1 Заданная схема Решение
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
|
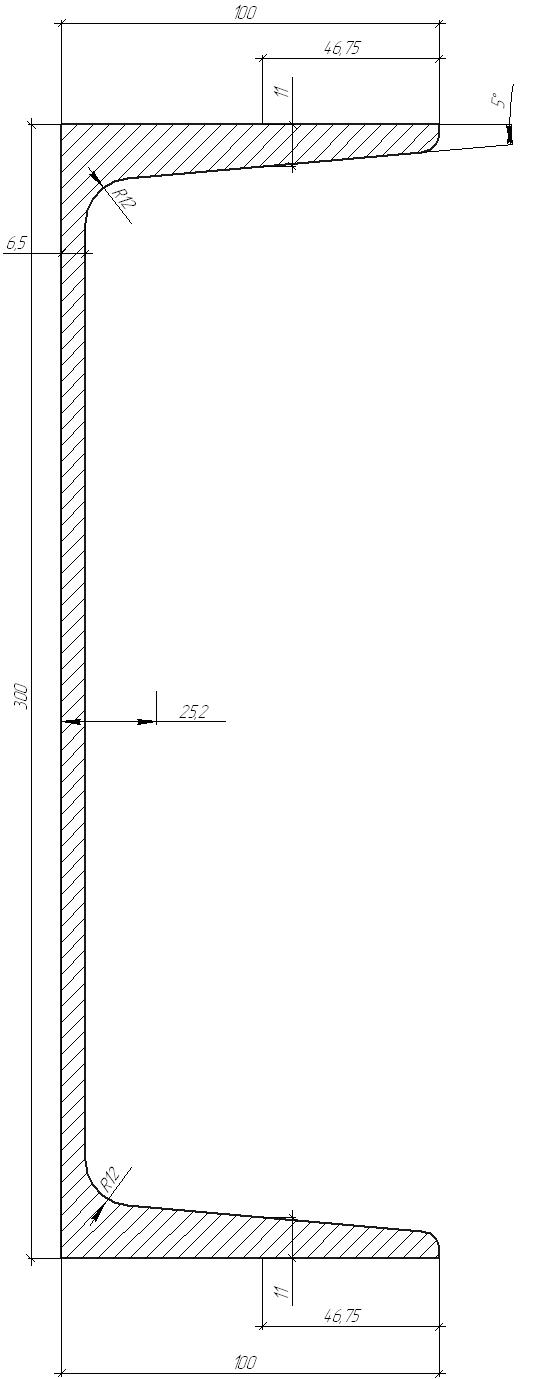
Задача 1 Стальной стержень (Е=2∙105 МПа) находится под действием продольной силы Р и собственного веса (γ=78 кН/м2). Найти перемещение сечения I-I (рис.1.1). Исходные данные: F= 20 см2; а=2,8 см; b=3,0 см; с=1,6 см; Р=1800 Н; 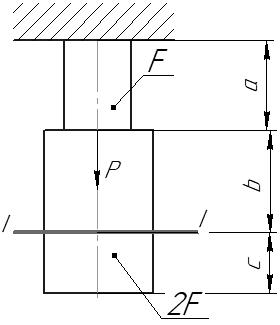 Рис.1.1 Заданная схема Решение Построим схему по заданным размерам и расставим силы 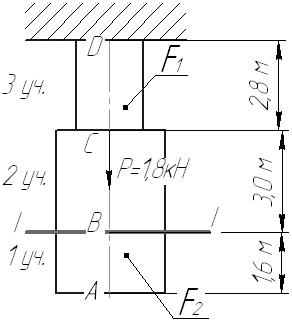 Вес стержня на каждом из участков  Построение эпюр продольных сил Участок АВ,  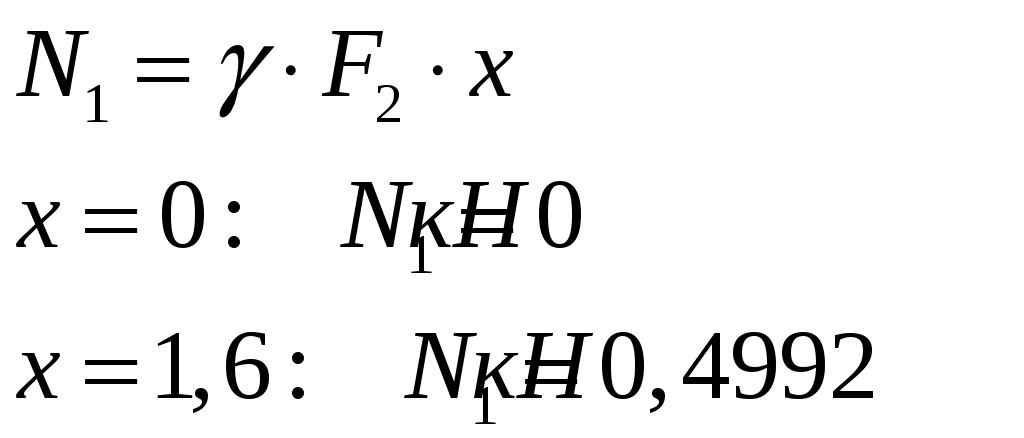 Участок СВ, 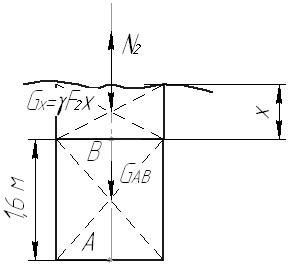 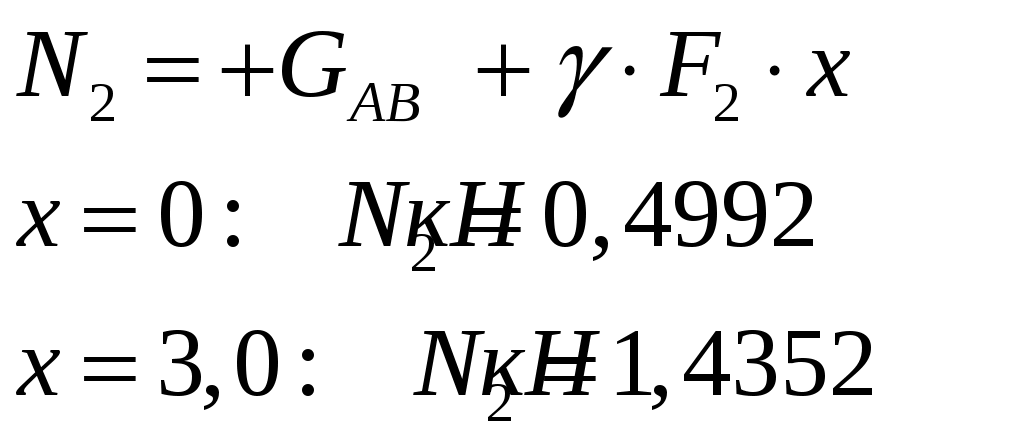 Участок СD, 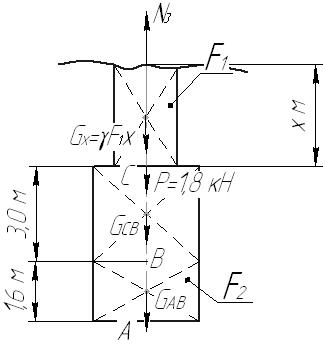 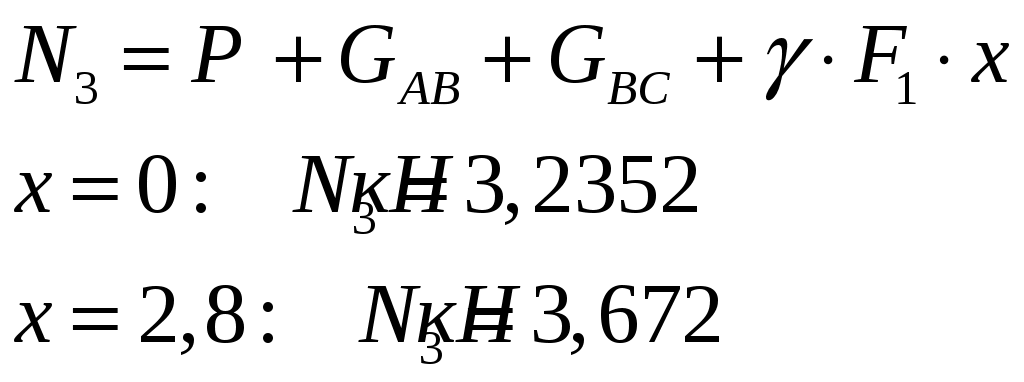 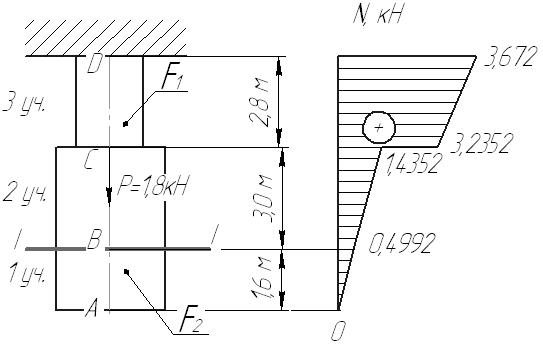 Наиболее опасные сечения: на участке АС – С, а на участке CD – D Напряжения в них  По условию прочности Условие выполняется Перемещение сечения I-I 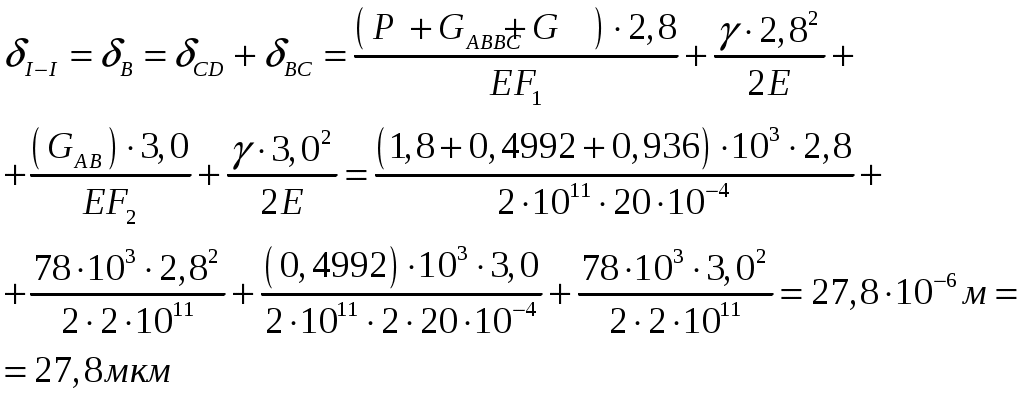 Задача 2 Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис.2.1). Требуется: найти усилия и напряжения в стержнях, выразив их через силу Q; найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ]=160 МПа; найти предельную грузоподъемность системы Q сравнить величины Qдоп, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам. Исходные данные: F= 20 см2; а=2,8 см; b=3,0 см; с=1,6 см 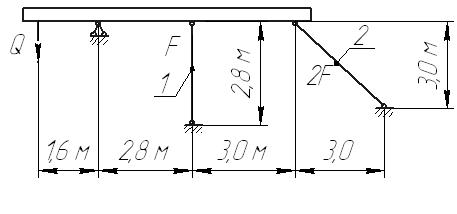 Рис.2.1 Заданная схема Решение Данная система статически неопределима один раз, поскольку четыре неизвестных (Nl,N2,Hk,Rk) не могут быть определены из трех независимых уравнений равновесия. Поэтому, кроме статической стороны задачи (рис. 1. 2, а), необходимо рассмотреть геометрическую (рис. 1.2, б) и физическую стороны задачи. 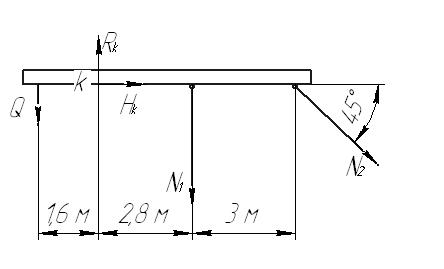 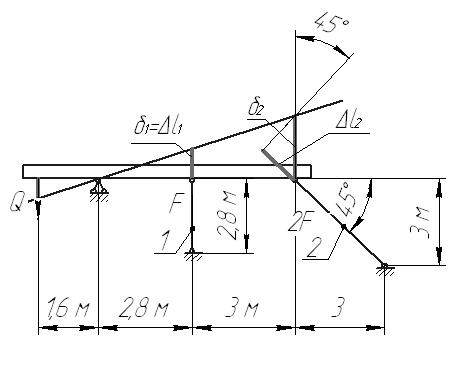 а Рис. 2.2 б Рассмотрение статической стороны задачи (см. рис. 1.2, а) дает следующее уравнение равновесия: ZMk= 0, Под действием силы Q жесткий брус повернется относительно шарнирно неподвижной опоры по часовой стрелке. Вследствие малости, перемещения характерных точек жесткого бруса по дугам окружностей можно заменить перемещениями по касательным к дугам окружностей. В нашем случае перемещение δ1 концевого сечения первого стержня совпадает с его продольной деформацией Δl1. Второй стержень, чтобы совместить начальное положение его концевого сечения с конечным, надо растянуть на Δ l2 и повернуть вдоль касательной по часовой стрелке (касательная будет перпендикулярна продольной оси второго стержня). При этом Из рис. 1.2, б следует: 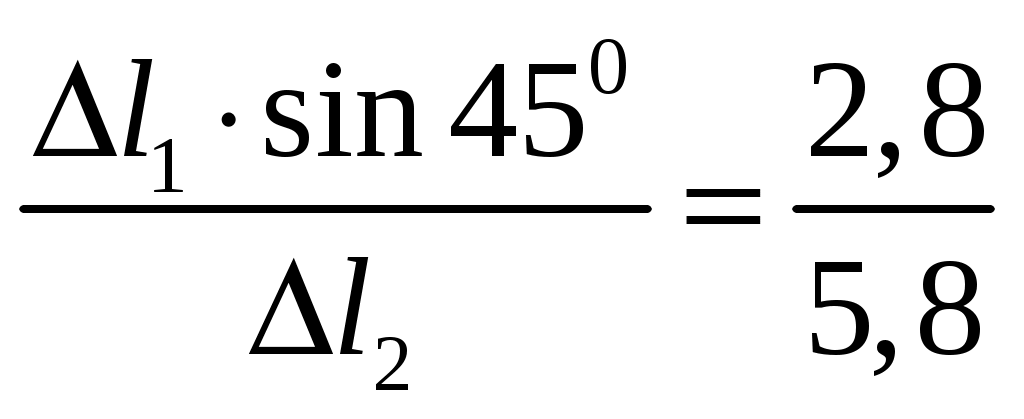 , отсюда , отсюда 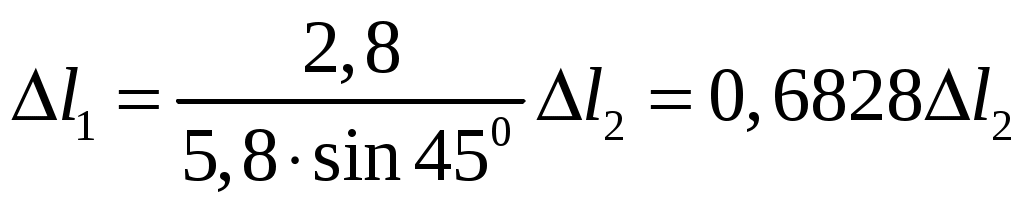 Здесь При составлении уравнения равновесия помним о соответствии статической стороны задачи геометрической, т. е. растягивающим деформациям должны соответствовать растягивающие усилия и наоборот. Выразить деформации стержней 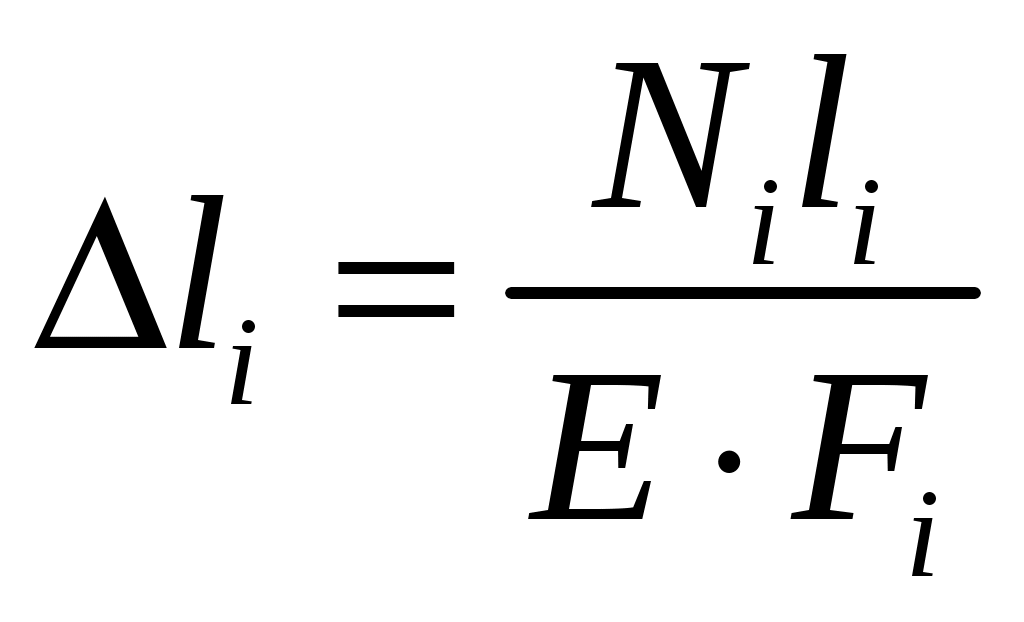 ): ):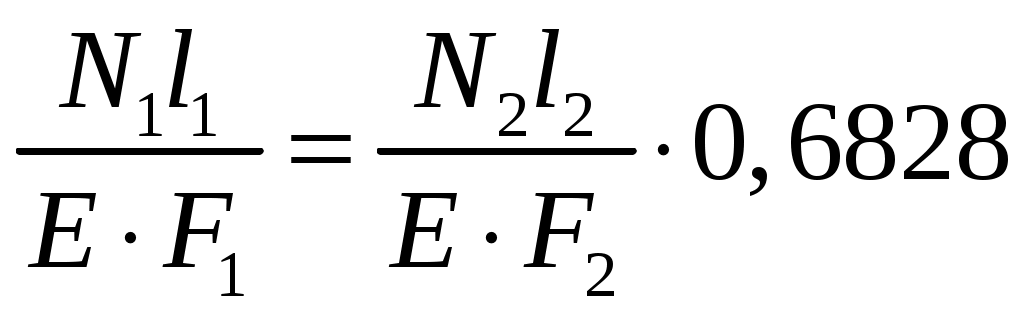 ; с учетом ; с учетом 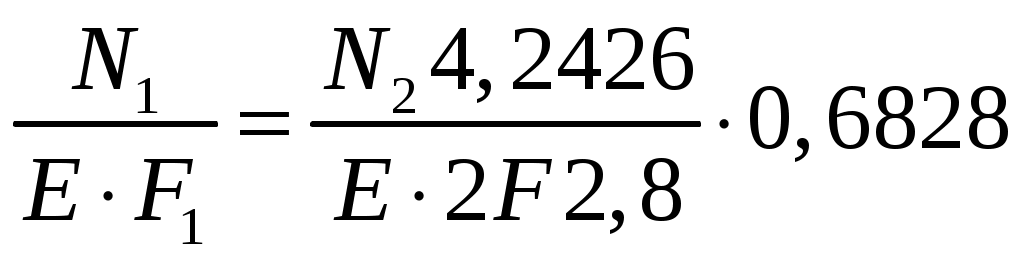 Имеем Решая совместно систему полученных уравнений, определим значения N1 и N2 в долях от Q:  , , 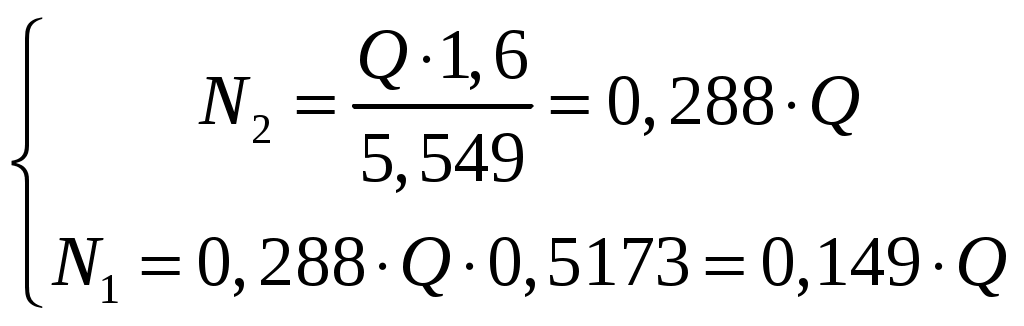 Напряжения в поперечных сечениях стержней 1 и 2 будут равны: 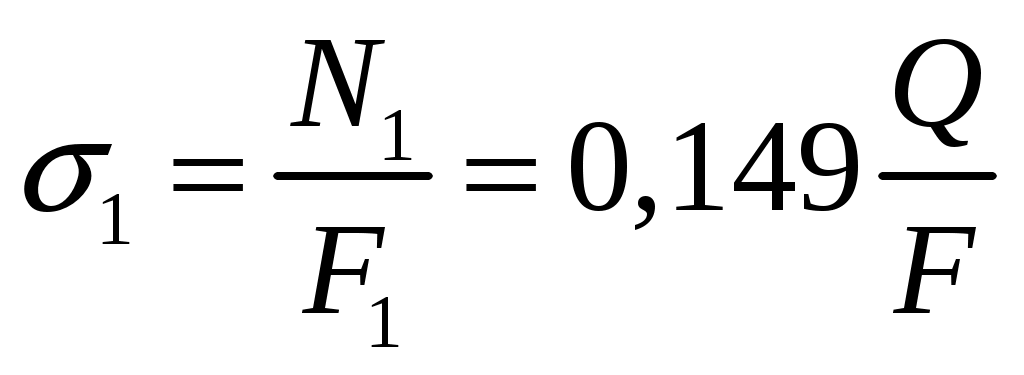 , , 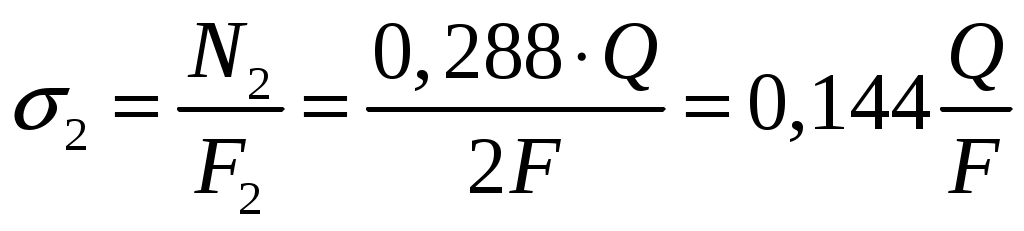 Допускаемую нагрузку находим из условия прочности по нормальным напряжениям, приравняв большее из напряжений в двух стержнях допускаемому напряжению: Предельную грузоподъемность системы ZMk= 0,  , , 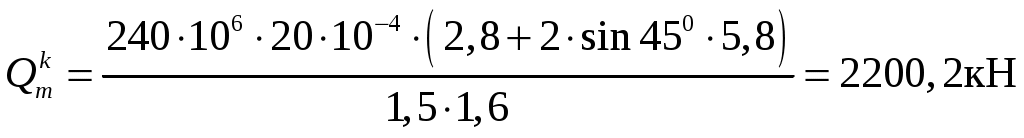 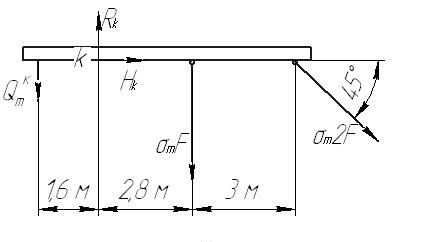 Рис. 2.3 Сравним величины Qдоп, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам Задача 5 К стальному валу приложены три известных момента: М1, М2, М3. Требуется: Установить при каком значении момента Х угол поворота правого концевого сечения вала равен нулю; Для найденного значения Х построить эпюру крутящих моментов; при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; построить эпюру углов закручивания; найти наибольший относительный угол закручивания (на 1 м). Исходные данные: а=1,8 см; b=2,0 см; с=1,6 см; М1=1800 Нм; М2=1000 Нм; М3=1600 Нм; τ=80 МПа; 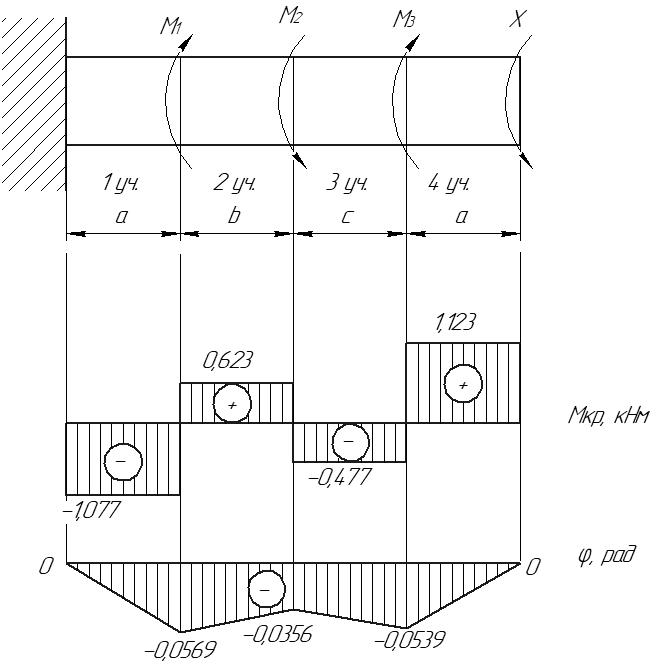 Рис.5.1 Заданная схема Решение Угол закручивания на каждом грузовом участке вала определяется по следующей формуле  (1) (1)где Mкрi −– крутящий момент на i-м грузовом участке; li – длина i−го грузового участка; G – модуль сдвига материала вала; Jρ – полярный момент инерции вала круглого поперечного сечения. Запишем выражения для крутящих моментов на каждом грузовом участке через величины М1, М2, М3, и X: Подставив полученные величины в выражение (1) и используя условие задачи, получим следующее значение неизвестного момента, приложенного к правому концу вала: 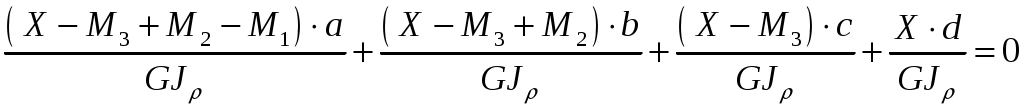 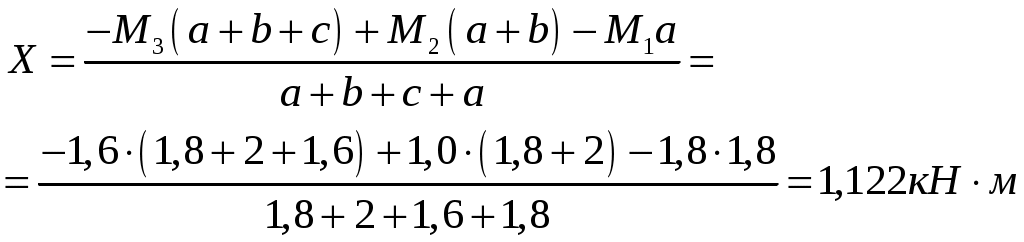 Знак «плюс» означает, что момент Х направлен в сторону, указанную в заданной схеме Используя выражения для крутящих моментов на каждом грузовом участке и полученное значение момента X, вычислим величины крутящих моментов на границах участков: 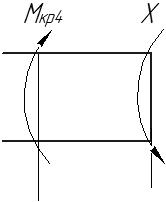 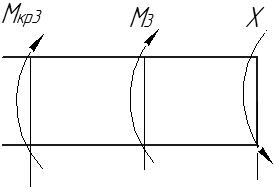  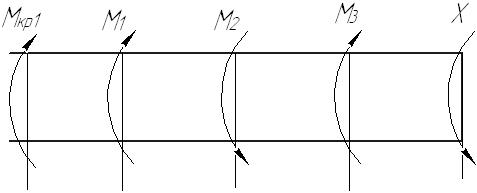 По полученным данным строим эпюру Мкр Запишем условие прочности вала при кручении:  (2) (2)где Mкр max− максимальное значение крутящего момента; Wρ − полярный момент сопротивления сечения вала. Полярный момент сопротивления круглого поперечного сечения определяется по формуле:  (3) (3)где d – диаметр вала. Тогда, используя выражения (2) и (3) получаем 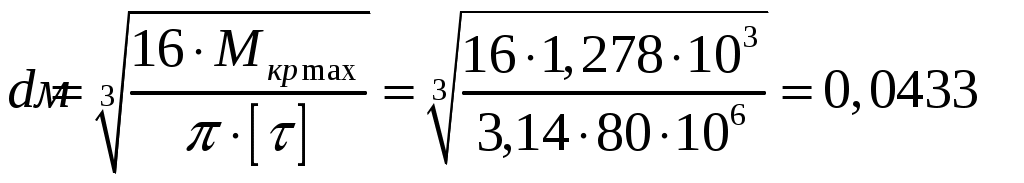 (4) (4)Окончательно принимаем диаметр вала d=45мм. Находим значение полярного момента инерции поперечного сечения вала по формуле 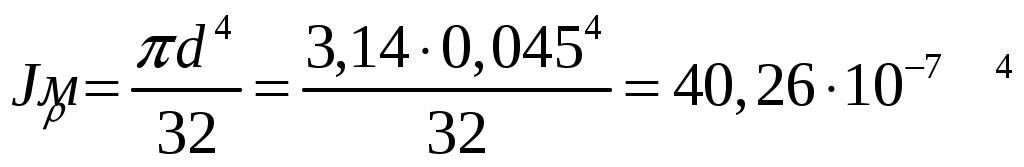 Используя формулу (1) и принимая величину модуля сдвига стали равной G=8⋅1010Па, вычисляем величину углов закручивания на каждом грузовом участке 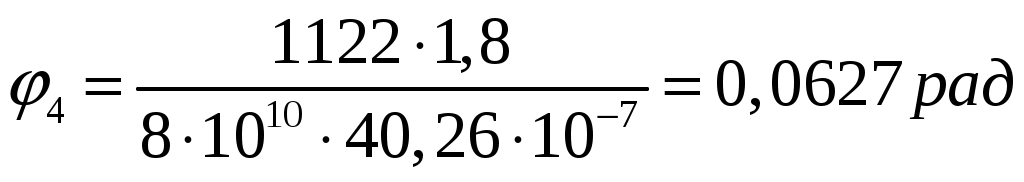  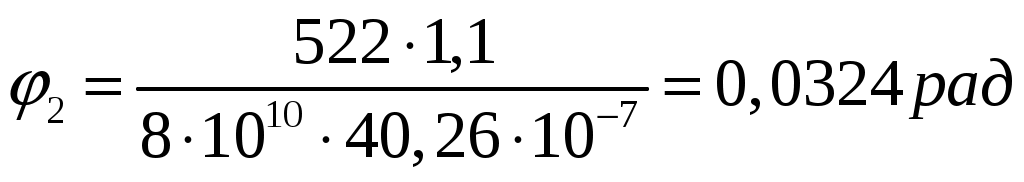 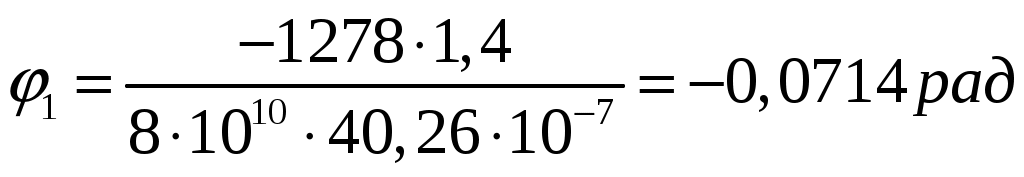 Определяем ординаты эпюры углов закручивания что соответствует условию задачи. По полученным значениям строим эпюру углов закручивания вала . Исходя из построенной эпюры , определяем наибольший относительный угол закручивания на 1 м его длины 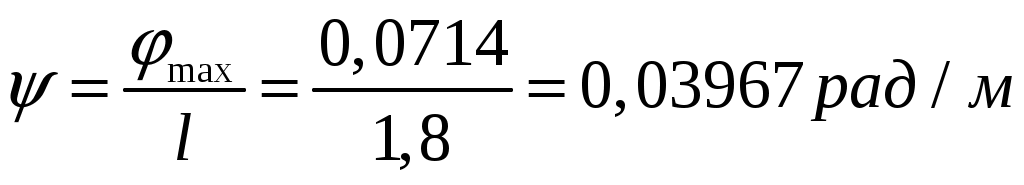 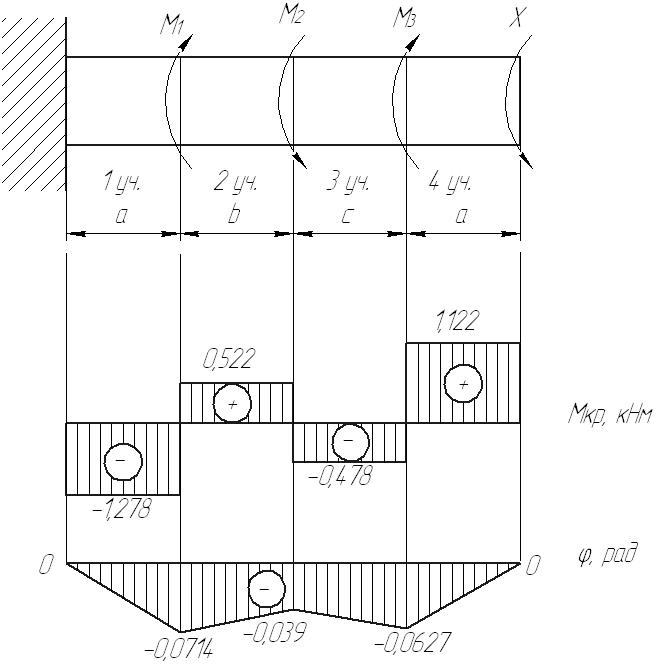 Рис. 5.2 Эпюры Задача 7 Для заданного поперечного сечения, состоящего из швеллера и равнобокого уголка или из двутавра и равнобокого уголка, или из швеллера и двутавра (рис.7.1), требуется: определить положение центра тяжести; найти осевые (экваториальные) и центробежный моменты инерции относительно случайных осей, проходящих через центр тяжести (zc и yc); определить направление главных центральных осей (u и v); найти моменты инерции относительно главных центральных осей; вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси. Исходные данные: Швеллер №30; равнобокий уголок 125х125х12 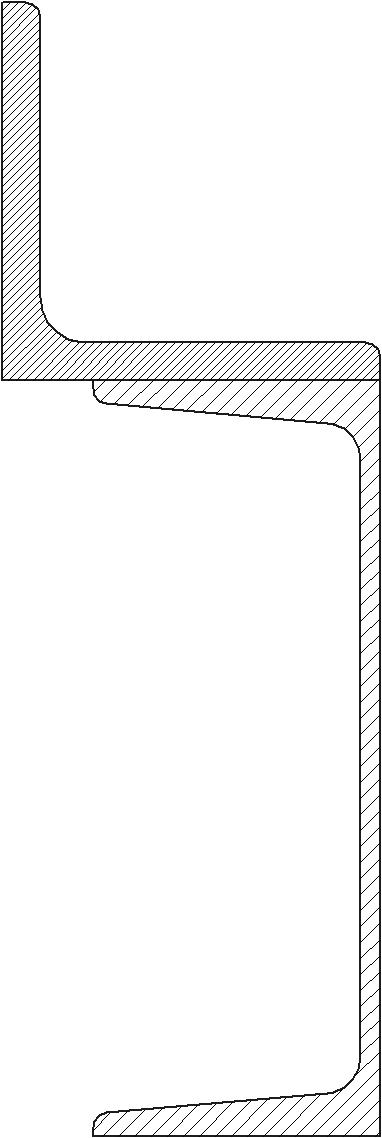 Рис.7.1 Заданная схема Решение Исходные данные:
1. Определим положение центра тяжести сечения, за расчётные примем оси крайнюю левую снизу точку сечения.  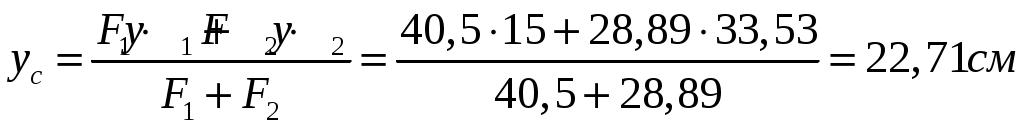 Центр тяжести находится на линии соединяющей центры тяжести частей 2. Определим моменты инерции относительно центральных осей. а) момент инерции относительно оси хС 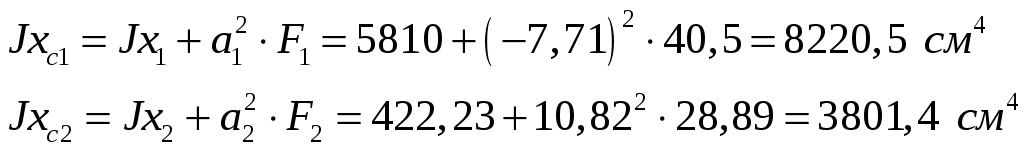 б) момент инерции относительно оси уС 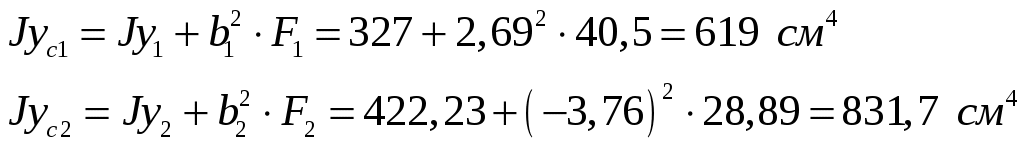 в) центробежный момент инерции Для уголка его собственные центральные оси 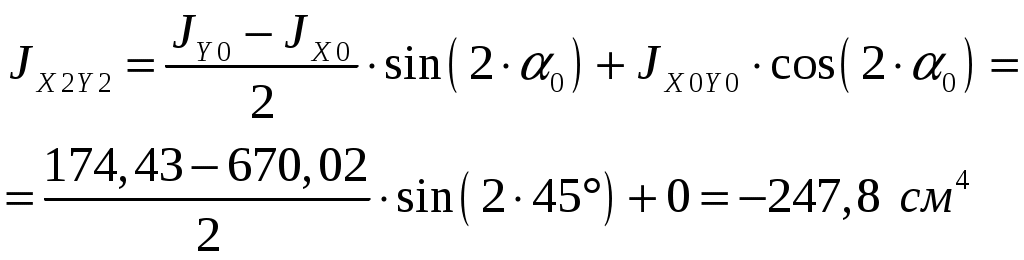  3. Определим положение главных центральных осей.  Т.к. 0 имеет положительное значение, то откладываем его против часовой стрелки. 4. Определим max и min значения главного момента инерции.  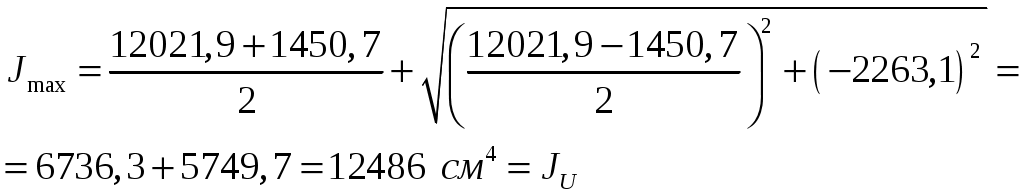 Проверка: 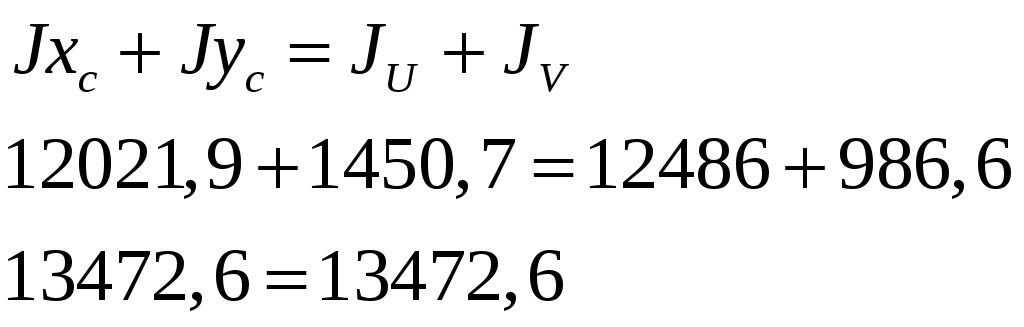 Строим сечение и откладываем, центры тяжести и все оси 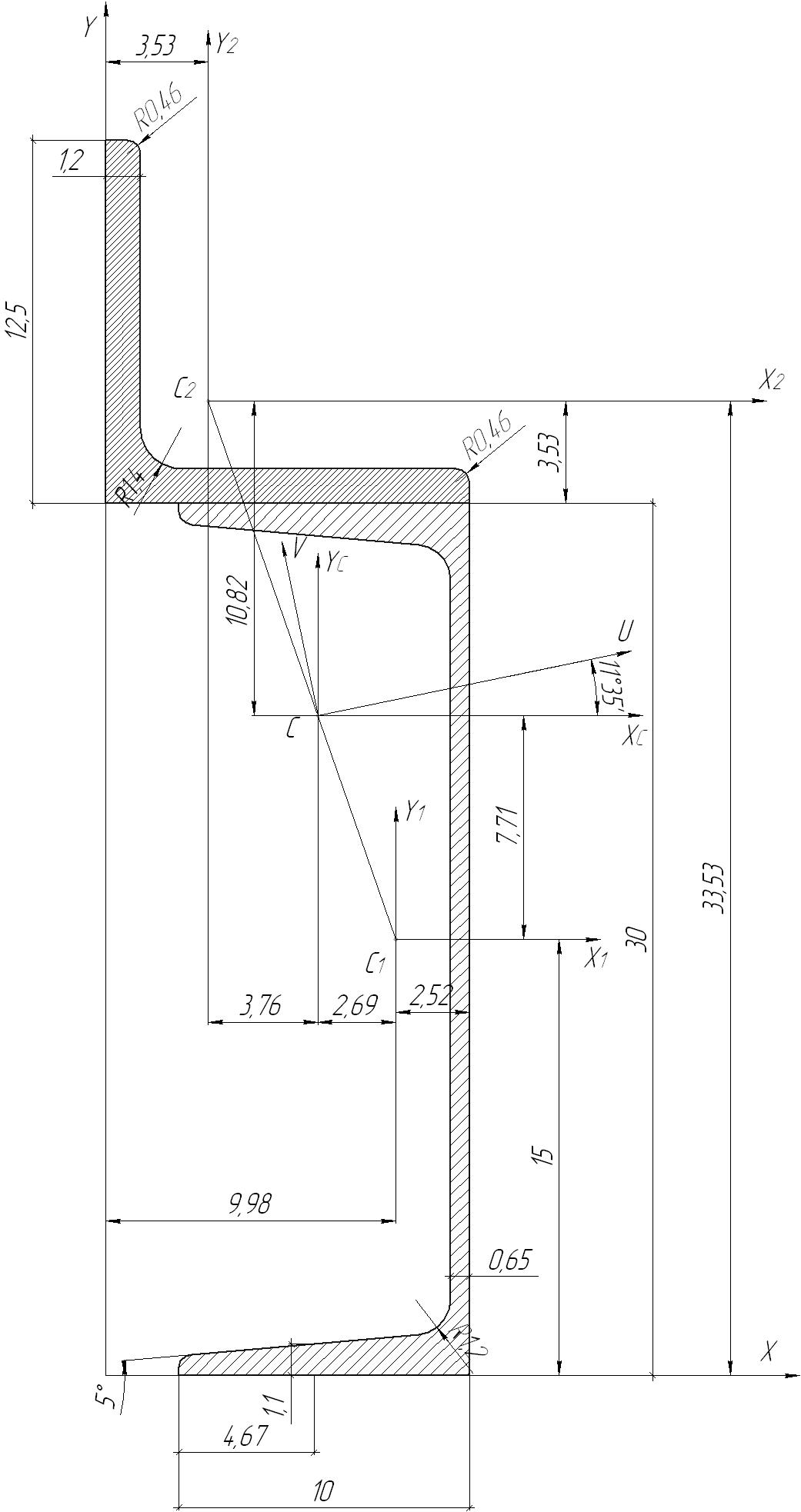 Рис. 7.2 Задача 8 Для заданных двух схем балок (рис.8.1) требуется написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти Мmax и подобрать: а) для схемы (а) деревянную балку круглого поперечного сечения при [σ]=8 МПа; б) для схемы (б) стальную балку двутаврового поперечного сечения при [σ]=160 МПа. Исходные данные: l1=2,0 м; l2=6 м; а1 /а=8; а2/а=10; а3 /а=1; М=8кНм; Р=10 кН; q=6кН/м 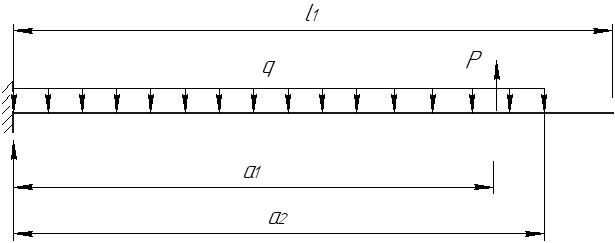 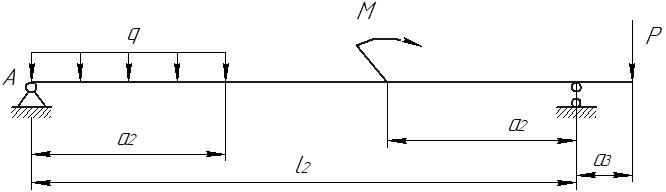 Рис.8.1 Заданные схемы Решение Схема а Построим сечение по заданным размерам с указанием всех нагрузок и сил 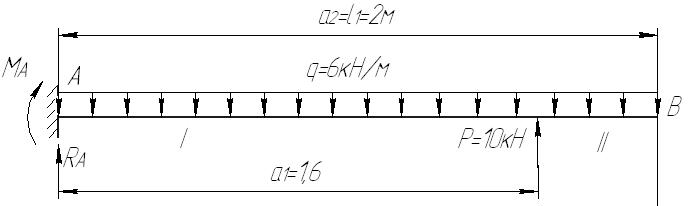 Рис.8.2 Реакции опор Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA =- MA- q a22/2 +Pa1 = - MA - 6·22/2 + 10·1.6 = - MA - 6·2·1 + 10·1.6 = = - MA + 4 = 0 ⇒ ⇒ MA = 4 кНм; Сумма проекций всех сил на вертикальную ось должна равняться нулю: ∑Y = RA - qa2 + P =RA - 6·2 + 10 = RA - 2 = 0 ⇒ ⇒ RA = 2 кН; Для проверки вычислим сумму моментов всех сил относительно точки B: ∑MB = - MA - RA l1 + q a2( l1 – a2/2) - P(l1- a1) = =-4 - 2·2 + 6·2 ·(2 - 2/2) - 10·(2 - 1.6) = -4 - 4 + 12 - 4 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках.
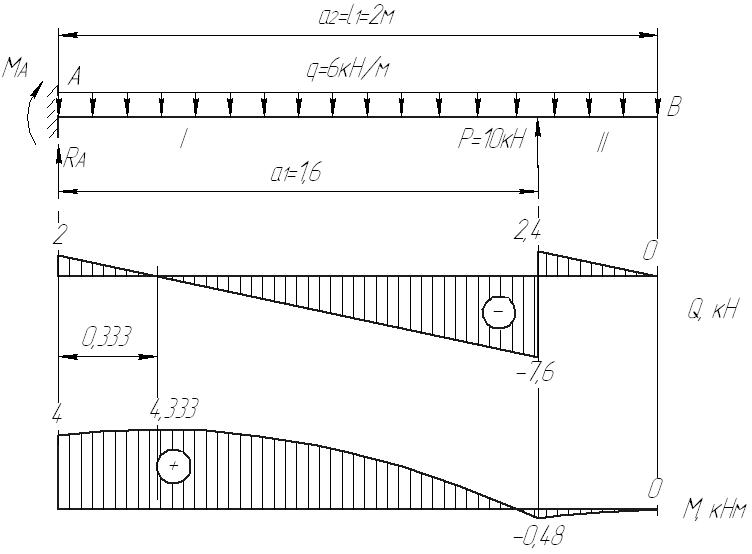 Рис.8.3 Опасное сечение на расстоянии 0,333м от защемления Осуществим подбор круглого сечения 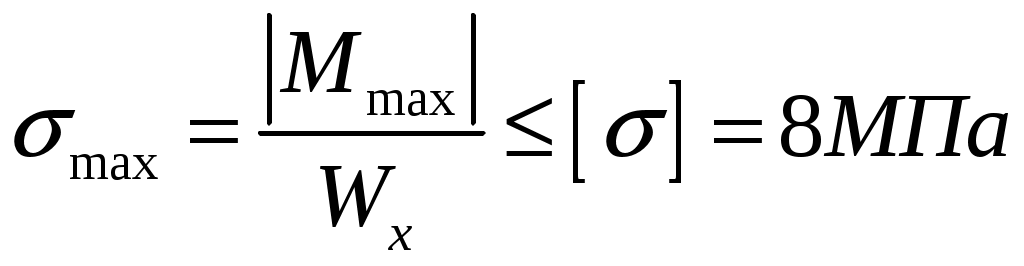 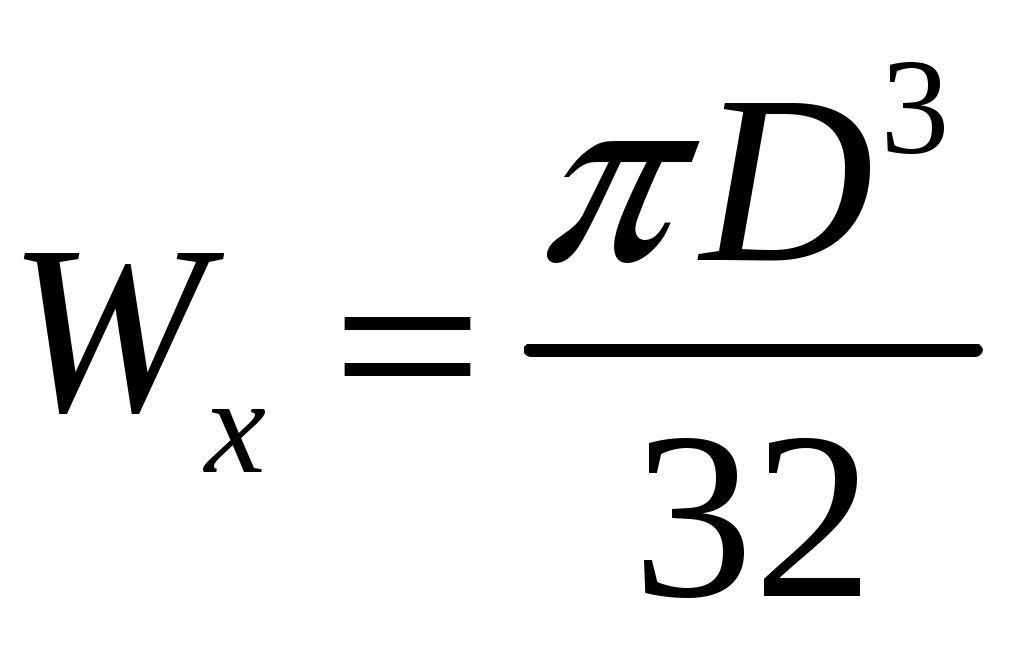 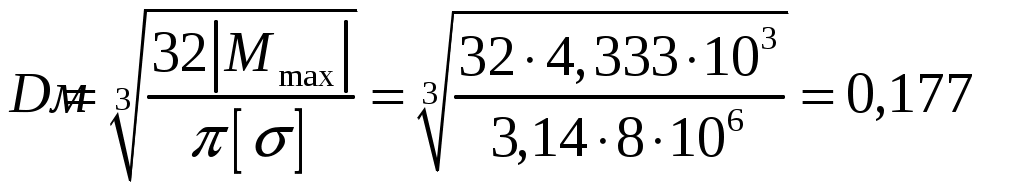 , принимаем 0,18 м , принимаем 0,18 мСхема б Построим сечение по заданным размерам с указанием всех нагрузок и сил 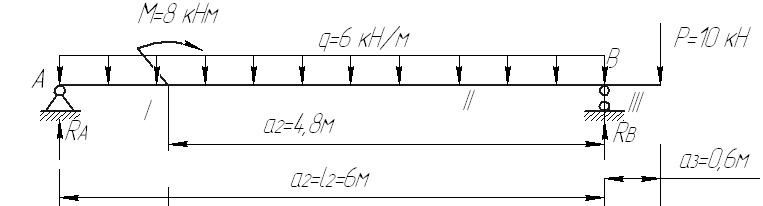 Рис.8.4 Реакции опор Сумма моментов всех сил относительно точки B должна равняться нулю: ∑MB = - RA l2 + qa2( l2 - a2/2) + Pa3 - M =- RA·6 + 6·6·(6 - 6/2) + 10·0.6 - 8 = = - RA·6 + 6·6·3 - 10·0.6 - 8 = - RA·6 + 94 = 0 ⇒ ⇒ RA = 94/6 = 15.6667 кН; Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB l2 - qa22/2 - P(l2 +a3) - M = RB·6 - 6·62/2 - 10·6.6 - 8 = = RB·6 - 6·6·3 - 10·6.6 - 8 = RB·6 - 182 = 0 ⇒ ⇒ RB = 182/6 = 30.3333 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = RA + RB - qa2 - P = 15.6667 + 30.3333 - 6·6 - 10 = = 15.6667 + 30.3333 - 36 - 10 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках.
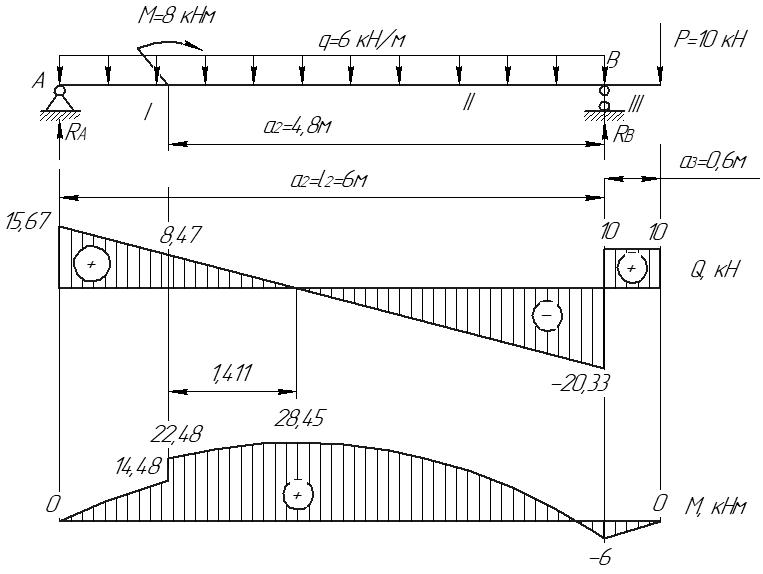 Рис.8.5 Опасное сечение на границе участков первого и второго участков Осуществим подбор двутаврового сечения 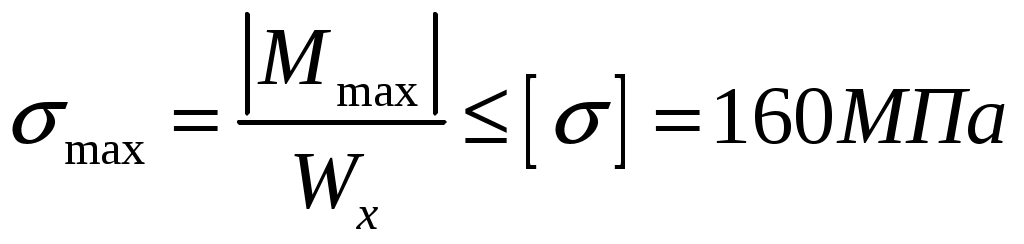 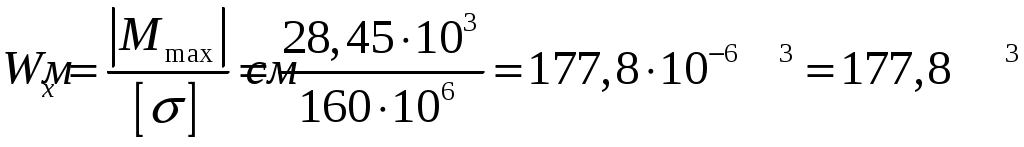 По сортаменту подбираем двутавр № 20 ГОСТ8239-97 Задача 10 Для балки, изображенной на рис.10.1, требуется: Найти изгибающий момента на левой опоре (в долях ql2); построить эпюры Q и М; построить эпюру прогибов, вычислив три ординаты в пролете и две на консоли. Исходные данные: α=0,8; β=1,0; k=6 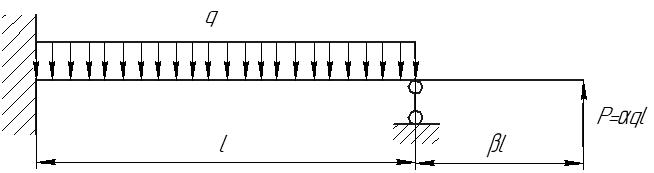 Рис.10.1 Заданная схема Решение При действии вертикальной нагрузки в данной балке возникают три опорные реакции: две в заделке – R0 и M0, и вертикальная реакция правой опоры RВ Для вычисления этих реакций мы можем составить всего два уравнения статики: ΣМ=0, ΣFy=0. Следовательно, система один раз статически неопределима. Отметим, что уравнение проекций на ось Х в данном случае составлять не имеет смысла, так как горизонтальных нагрузок в балке нет. Для вычисления R0 и M0 составим систему двух уравнений – сумму моментов относительно точки В и уравнение метода начальных параметров для определения прогиба балки в сечении над опорой В, который в действительности равен нулю. В обоих уравнениях реакция RВ отсутствует. ΣМВ=0 Уравнение прогибов в точке В имеет вид: 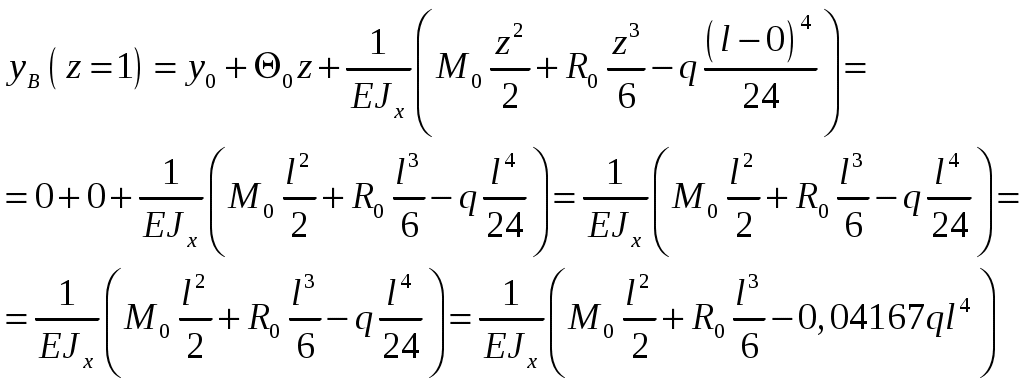 Разделим обе части последнего уравнения на 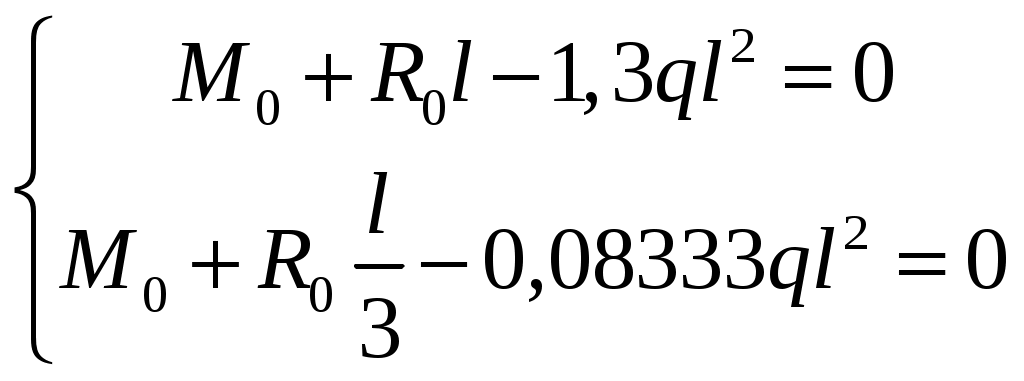 Вычтем из первого уравнения второе, получим Подставим R0 в первое уравнение системы (не имеет значения, можно и во второе подставить): Составим уравнение проекций на ось Y для вычисления опорной реакции RВ. R0+RB+P+F-ql =0, откуда: RB= -R0-P-F+ql = -1,825ql -0,8ql+ql= -1,625 ql Все опорные реакции найдены. Запишем выражения для поперечных сил и изгибающих моментов на участках балки. Участок 1. Заходим слева. 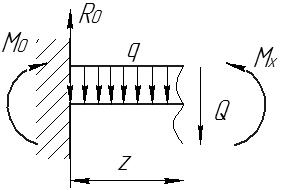 Рис.10.2 Поперечная сила: При z=0 При z=0,5l При z=l Изгибающий момент: При z=0 При z=0,5l При z=l Участок 2. Заходим справа.  Рис.10.3 Поперечная сила: Изгибающий момент: При z=0 При z=0,8l Выполним проверку построенных эпюр поперечных сил и изгибающих моментов. На первом участке балки действует равномерно распределённая нагрузка. Эпюра поперечной силы имеет вид наклонной прямой, убывающей слева направо, а эпюра моментов изменяется по закону квадратной параболы, выпуклостью вверх, т.е навстречу действия нагрузки. На границе первого и второго участков эпюра моментов имеет излом от реакции опоры. На втором участке, где распределённая нагрузка отсутствует, поперечная сила постоянна, а изгибающий момент изменяется по линейному закону. Построим эпюру прогибов, вычислив три ординаты в пролете и две – на консоли. Вычисление прогибов в пролёте балки Пролет балки разбиваем на четыре участка с границами: z=0,5; 0,5l; 0,5l; l. Вычисляем прогибы с помощью метода начальных параметров. Запишем уравнение прогибов на первом участке (рис. 2): 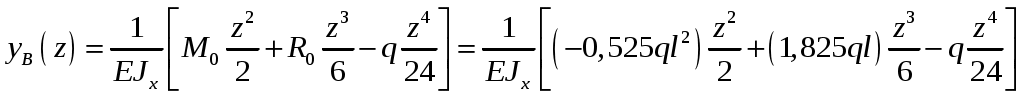 Вычислим прогибы в сечениях первого участка: 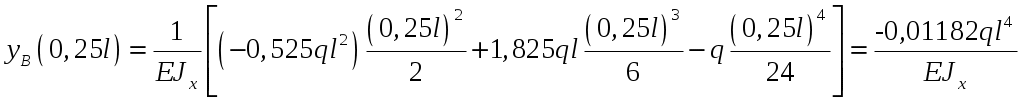 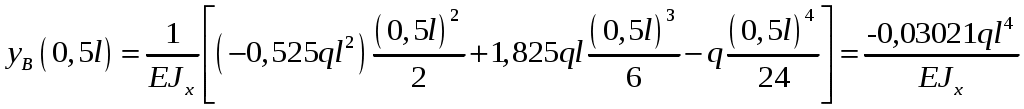 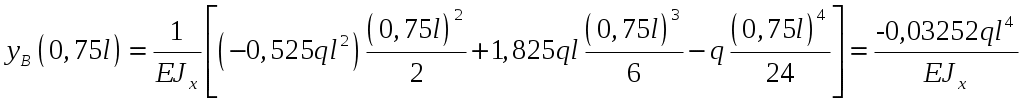 Отрицательный прогиб вниз. 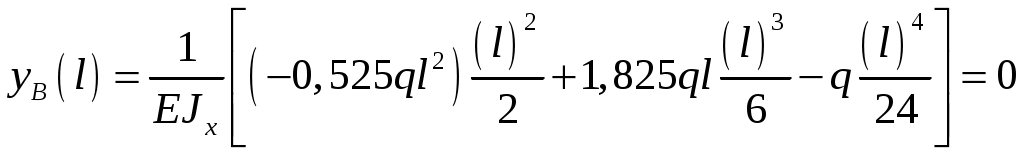 как и должно быть на опоре. 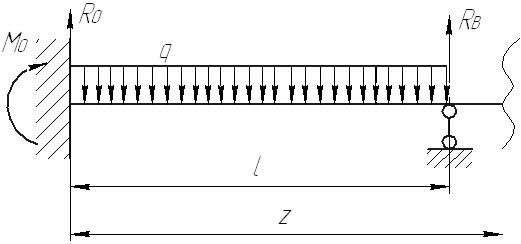 Рис.10.4 Уравнение прогибов на консоли: 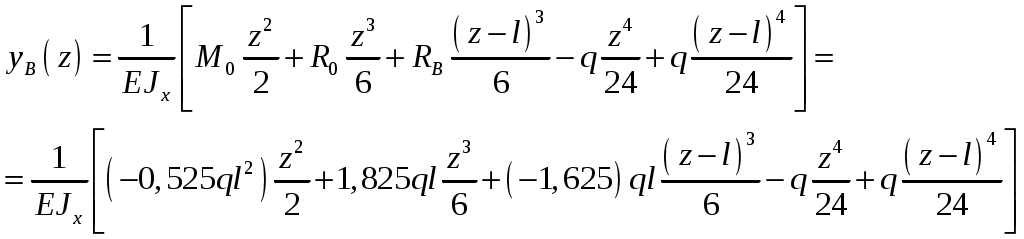 Прогиб в середине консоли при z=1,5l: 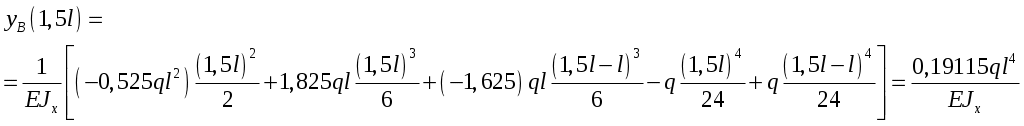 Прогиб в конце консоли при z=2,0l: 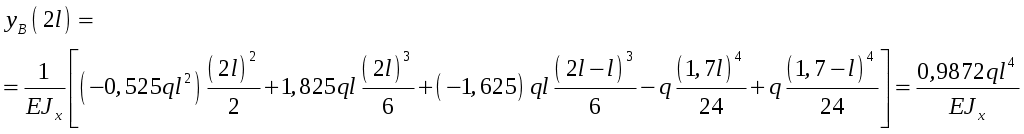 Эпюра прогибов (или искривление оси балки под нагрузкой) показана на рисунке 10.5. Следует отметить, что точки перегиба эпюры прогибов соответствуют сечениям балки, в которых значение изгибающего момента равно нулю. На участках балки, где эпюра моментов отложена на верхних волокнах, эпюра прогибов имеет выгиб вверх, что соответствует растяжению сверху. И наоборот, на участке, где эпюра моментов отложена снизу, ось балки выгнута вниз. Сечения балки, близкие к заделке, не испытывают прогибов и углов поворота.  Рис.10.5. Эпюры поперечных сил, изгибающих моментов и прогибов |