пример. лист1. 2 синтез зубчатого передаточного механизма
 Скачать 268.55 Kb. Скачать 268.55 Kb.
|
 2 СИНТЕЗ ЗУБЧАТОГО ПЕРЕДАТОЧНОГО МЕХАНИЗМА (лист 1 графической части проекта) В данном курсовой работе зубчатый механизм состоит из планетарного механизма типа AI-2 и пары прямозубых цилиндрических колес внешнего зацепления (z5, z6) и служит для передачи вращательного момента от вала электродвигателя к валу кривошипа и получения заданной частоты вращения кривошипа. Рисунок 2.1-Схема привода исполнительного механизма 2.1 Синтез эвольвентного зубчатого зацепления Исполняем синтез зубчатого зацепления парой эвольвентных цилиндрических прямозубых колес внешнего зацепления z5 и z6 (см лист 1 курсовой работы). 2.1.1 Исходные параметры синтеза, выбор коэфициентов смещения Для расчета геометрических параметров эвольвентного зацепления используем такие исходные параметры: - число зубьев шестерни z5 =14; - число зубьев колеса z6 = 16; - модульm5-6 = 7 мм; -условия проэктирования Ơ1=Ơ2 при ε=1.2; - коэффициенты смещения шестерни х5 = 0,42;и колеса х6 = 0,44. Значения коэфициентов смещения для шестерни и колеса выбираем с помощью блокирующего контура (рис 1.2), исходя из заданного условия получения максимально возможной износостойкости зубьев колеса и шестерни при значении коэфициента торцевого перекрытия εa=1.2.  Рисунок 1.2 –Блокирующий контур   Допустим, что для нарезания колес будет использован инструмент реечного типа с нормальным исходным контуром ГОСТ 13755-81, Допустим, что для нарезания колес будет использован инструмент реечного типа с нормальным исходным контуром ГОСТ 13755-81,Параметры которого: - угол профиля зубьев = 20 ; - коэффициент высоты головки зуба  = 1; = 1;- коэффициент граничной высоты  = 2; = 2;- коэффициент радиального зазора с* = 0,25. 2.1.2 Расчет геометрических параметров качественных показателей зацепления с помощью ПЭВМ Расчет параметров зубчатого зацепления выполнен с помощью ПЭВМ по приведенным ниже расчетным зависимостям [1]. 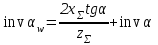 , (2.1) , (2.1)где  ; ; 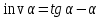 ; z= z5 + z6 . ; z= z5 + z6 .Уравнение (1.1) решено относительно w методом последовательных приближений. Межосевое расстояние зацепления: 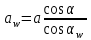 , (2.2) где , (2.2) где 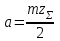 - делительное межосевое расстояние. - делительное межосевое расстояние.Делительные диаметры колес:  (i=5,6). (2.3) (i=5,6). (2.3)Начальные диаметры колес:  (i = 5,6). (2.4) (i = 5,6). (2.4)Основные диаметры колес: 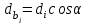 , (i = 5,6). (2.5) , (i = 5,6). (2.5)Диаметры впадин колес: 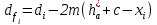 , (i = 5,6). (2.6) , (i = 5,6). (2.6)Диаметры вершин колес 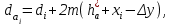 (i = 5,6), (2.7) (i = 5,6), (2.7)где  - коэффициент уравнительного смещения; - коэффициент уравнительного смещения; - коэффициент воспринимаемого смещения. - коэффициент воспринимаемого смещения.Окружной делительный шаг зубьев:  (2.8) (2.8)Окружной основной шаг зубьев: 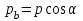 (2,9) (2,9)Окружной начальный шаг зубьев: 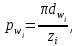 (i = 5,6). (2.10) (i = 5,6). (2.10)Толщины зубьев по делительным окружностям:  , (i = 5,6). (2.11) , (i = 5,6). (2.11)Толщины зубьев по основным окружностям 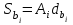 , (i = 5,6), (2.12) , (i = 5,6), (2.12)где  . .Толщины зубьев по начальным окружностям: 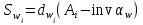 , (i=5,6). (2.13) , (i=5,6). (2.13) , ,Углы профилей зубьев колес в точке на окружности вершин: 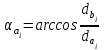 , (i=5,6). (2.14) , (i=5,6). (2.14)Толщины зубьев по окружности вершин: 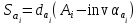 , (i = 5,6). (2.15) , (i = 5,6). (2.15)Радиусы кривизны активного профиля зубьев колеса в нижней точке: 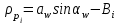 , (i = 5,6), (2.16) , (i = 5,6), (2.16)где  Радиусы кривизны в граничных точках профилей зубьев колес: 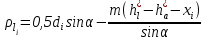 , (i = 5,6). (2.17) , (i = 5,6). (2.17)Коэффициент торцового перекрытия: 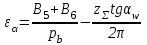 , (i = 5,6). (2.18) , (i = 5,6). (2.18)Результаты машинного расчета приведены в табл. 4.1. По ним составлена сводная таблица параметров зацепления (см. лист 2 графической части проекта). Коэффициенты удельного скольжения в контактных точках зубьев: - для шестерни  - для колеса 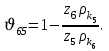 Определение значений 56 и 65 для положений контактной точки 1…9 на теоретической линии зацепления АВ при делении ее на 10 равных частей и нумерации, начинающейся с 0, произведено с помощью ПЭВМ.  Результаты расчета см. в табл. 1.1. В точке 0: 56 = -; 65 = 1. В точке 10: 56 = 1; 65 = -.    2.1.3 Проверочные расчеты Для проверки правильности результатов, полученых на ПЭВМ, проведем такие расчеты. Проверка межосевого растояния и начальных диаметров колес:  мм (2.19) мм (2.19)110.18 мм=110.18 мм-верно Проверка диаметров окружностей вершин и окружностей впадин: 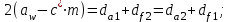 (2.20) (2.20)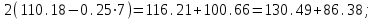 216.87 мм=216.87 мм=216.87 мм-верно. Проверка начальных толщин зубов колес и начального окружного шага: 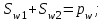 где где  =23.08 мм; (2.21) =23.08 мм; (2.21)11.63+11.43=23.08 мм-верно Проверка выбора коэфициентов смещения; Подрезание зубьев отсутствует при 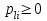 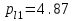 мм >0 –подрезания нет мм >0 –подрезания нет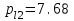 мм >0 –подрезания нет мм >0 –подрезания нет Заострение зубьев отсутствует при 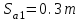 . (2,22) . (2,22)0,3m=0.3·7=2.1 мм;  >2,1 мм –заострение отсутствует; >2,1 мм –заострение отсутствует;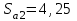 >2,1 мм –заострение отсутствует; >2,1 мм –заострение отсутствует;Заклинивание(интерференция зубьев) отсутствует при 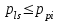 . . -интерференции нет; -интерференции нет;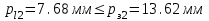 -интерференции нет; -интерференции нет;Исходя из правильности проверки, делаем вывод про то, что расчет зубчатой пары выполнен верно.  2.1.4 Построение картины зацепления и диаграмм коэффициентов удельного скольжения По данным табл. 1.1 на листе 1 графической части роботы в масштабе M 4:1   ) строим картину эвольвентного зацепления, изобразив по три зуба каждого из колес, и диаграммы коэффициентов удельного скольжения 56 и 65 в прямоугольной (на линии параллельной теоретической линии зацепления АВ) и в круговой (на рабочих профилях зубьев) системах координат. ) строим картину эвольвентного зацепления, изобразив по три зуба каждого из колес, и диаграммы коэффициентов удельного скольжения 56 и 65 в прямоугольной (на линии параллельной теоретической линии зацепления АВ) и в круговой (на рабочих профилях зубьев) системах координат.На построенную картину зацепления наносим: 1) рабочую часть линии зацепления ab; 2) рабочие участки профилей зубьев; 3) рабочие профили в момент начала и в момент конца зацепления; 4) дуги зацепления по начальным окружностям; 5) углы перекрытия 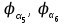 и угловые шаги 5, 6 ; и угловые шаги 5, 6 ;6) линии зацепления n-n для обоих возможных направлений вращении колес.  |
