Лекция. Основы тригонометрии. Лекция Основы тригонометрии. Градусное и радианное измерение углов
 Скачать 69.27 Kb.
|
Радианная мера любого угла АОВ есть отношение длины дуги АВ, описанной произвольным радиусом из центра О и заключенной между сторонами угла, к радиусу ОА этой дуги.
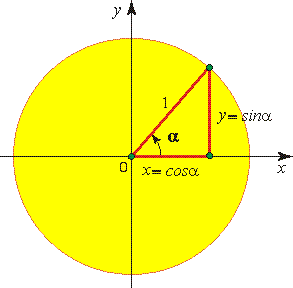
А° — угол в градусах, α — угол в радианах. Градусная мера угла в 1 радиан равна: Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.  Так как π = 3,14, то 1 рад = 57,3° Если угол содержит α радиан, то его градусная мера равна  И наоборот  1 рад ≈ 57,29578 °. 1° ≈ 0,017453 рад. 1' ≈ 0,000291 рад. 1'' ≈ 0,0000048 рад. Пример 1. Найти радианную меру угла равного 1) 30°, 2)135° Решение: 1) 30° = 30·π / 180 = π/6 2) 135° = 135·π/180 = 3π/4 Пример 2. Найти градусную меру угла выраженного в радианах 1) π/3 , 2) 4·π/5 Решение: 1) π/3 = 180°/3 = 60° 2) 4π/5 = 4·180°/5 = 144° ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе. Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему. Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему. Угла поворота В тригонометрии на угол начинают смотреть более широко - вводят понятие угла поворота. Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞ до +∞. В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины - угла поворота. Они даются через координаты x и y точки A1, в которую переходит так называемая начальная точкаA(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности. 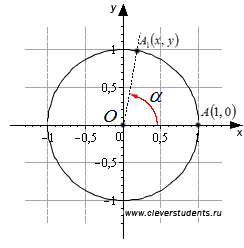 Синус угла поворота α - это ордината точки A1, то есть, sinα=y. Косинусом угла поворота α называют абсциссу точки A1, то есть, cosα=x. Тангенс угла поворота α - это отношение ординаты точки A1 к ее абсциссе, то есть, tgα=y/x. Котангенсом угла поворота α называют отношение абсциссы точки A1 к ее ординате, то есть, ctgα=x/y. Синус и косинус определены для любого угла α, так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α. А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α, при которых начальная точка переходит в точку с нулевой абсциссой (0, 1) или (0, −1), а это имеет место при углах 90°+180°·k, k∈Z (π/2+π·k рад). Действительно, при таких углах поворота выражение tgα=y/x не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α, при которых начальная точка переходит к в точку с нулевой ординатой (1, 0) или (−1, 0), а это имеет место для углов 180°·k, k∈Z (π·k рад). Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k, k∈Z (π/2+π·k рад), а котангенс – для всех углов, кроме 180°·k, k∈Z (π·k рад).
Окружность с центром в начале координат, радиус которой равен 1, называется единичной окружностью. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
Основные тождества:  Знаки тригонометрических функций:  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
часть полного оборота вокруг своей начальной точки против часовой стрелки ;
часть градуса; 
.
