2. Вычислить пределы последовательностей
 Скачать 43.13 Kb. Скачать 43.13 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ _________Математика____________________________________________ Группа Во21ГУ171В ______ Студент Васичева Лада В. МОСКВА 2021___ 1. Выполнить деление комплексных чисел. 1.1 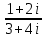 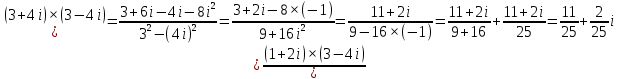 1.2 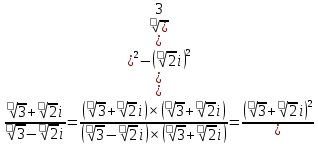  2. Вычислить пределы последовательностей. 2.1 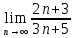 Приведем выражение под знаком предела к очевидному виду. Делим каждый член выражения на n. 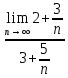 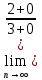 = =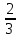 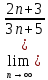 = =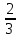 2.2 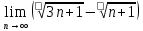 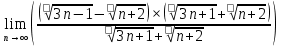 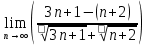 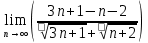 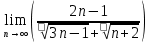 Ответ: Выражение определено как 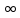 . .3. Используя признаки Даламбера и Коши исследовать сходимость рядов. 3.1 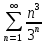 По Даламберу рассмотрим отношение общего последующего члена ряда к предыдущему члену ряда и найдем предел этого отношения. 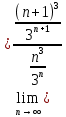 |) |)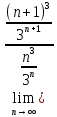 ) )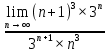 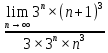 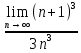 Применяем формулу сокращенного умножения. 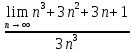 Делим каждый член выражения на 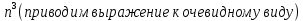 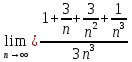 | |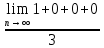  Ответ: Так как значение предела меньше 1, ряд сходится абсолютно. 3.2 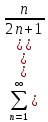 По признаку Коши ищем 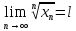 В нашей задаче 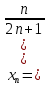 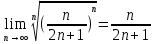 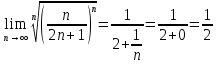 Ответ: выражение 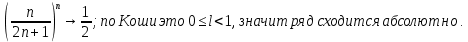 4. Найти производные функций. 4.1 y=sin(lnx) По формуле для производной сложной функции (f(g( 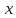 )))x )))x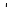 =f'g (g( =f'g (g(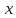 )) ))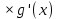 g(x) внутренняя функция, здесь g(x)=lnx f(g) внешняя функция, здесь f(g)=sin(g) Сначала по таблице производных находим g'(x)= (lnx)'x = 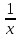 По таблице производных находим f'(g)=(sing) g ' = cosg Полученные производные подставляем в формулу: (f(g(x)))x '=cos g 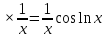 Ответ: Производная от сложной функции y=sin ln x определяется так (sin ln x)'= 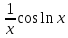 4.2 y=ln 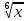 1) g(x)= 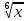 f(g)= ln g 2) f((g(x)))x ' = f'g (g(x)) 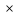 g'(x) g'(x)3) g'x (x)=( 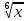 )x '= ( )x '= (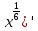 x = x =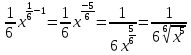 4) f'g(g)=(lng)'g = 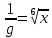 5) Подставим значения производных. y' =(ln 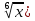 x '= x '=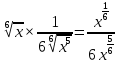 = =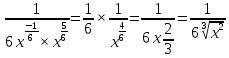 Ответ: (ln 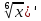 x = x = 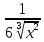  5. Вычислить неопределённый интеграл. 5. Вычислить неопределённый интеграл.5.1 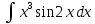 = =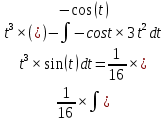 = =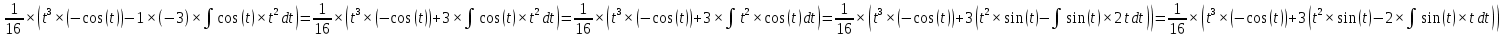 = =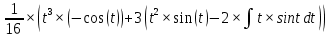 = =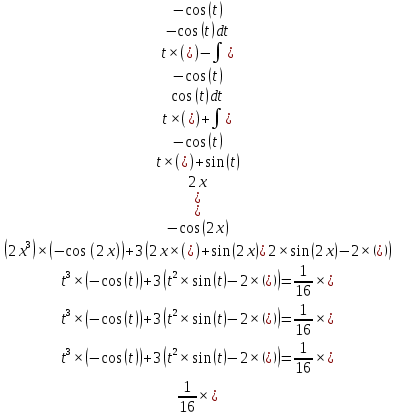 = =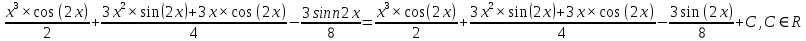 5.2 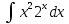 u= 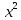 dv= 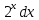 du=2xdx v= 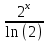 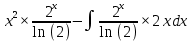 = = 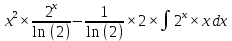 = =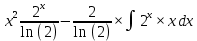 = =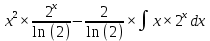 = =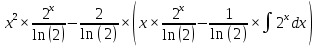 = =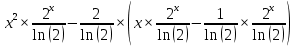 = =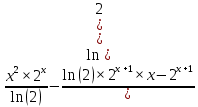 +C, C +C, C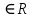 6. Найти производные первого и второго порядка. 6.1 z= 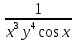 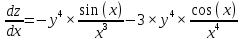 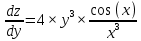 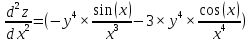 'x 'x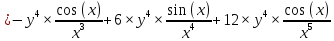 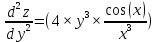 'y 'y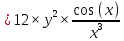 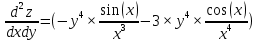 'y 'y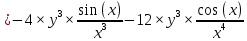 6.2 z= 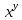 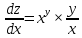 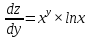 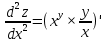 x x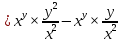 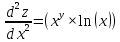 'y 'y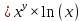 2 27. Найти сумму матриц. 7.1 А= 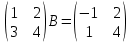 A+B= 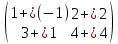 = = 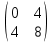 7.2 A= 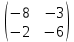 B= B= 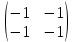 A+B= 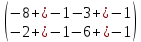 = =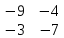 8. Найти произведение матриц. 8.1 A= 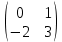 B= B=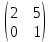 A 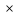 B= B=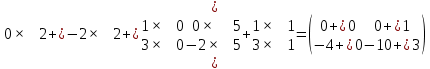 = =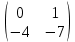 8.2 A= 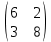 B= B=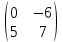 A 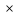 B= B= 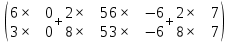 = =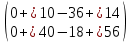 = = 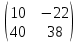 9. Найти определители матриц. 9.1. A= 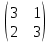 |A|= 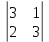 = 3 = 3 3-1 3-1 2=9-2=7 2=9-2=7Ответ: |A|=7 9.2. A= 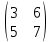 |A|= 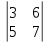 =3 =3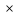 7-6 7-6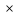 5=21-30=-9 5=21-30=-9Ответ: |A|=-9 10. Решить систему уравнений. 10.1. 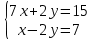 1) Сложим почленно 1 и 2 уравнения. 8x=22 x= 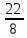 x= 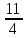 2) Из 1 уравнения найдём y. 2y=15-7x y= 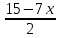 3) Подставим значение x в выражение для y. y= 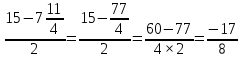 Ответ: x= 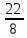 ; y= ; y=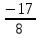 10.2. 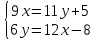 6y=12x-8 6y-12x=-8 -12x=-8-6y x=  Подставим значение x в уравнение 9x=11y+5 9 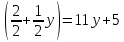 6+ 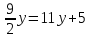 Умножим обе части на 2 12+9y=22y+10 9y-22y=10-12 -13y=-2 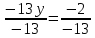 y= 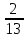 x= 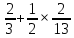 x= 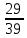 Ответ: x= 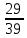 ; y= ; y=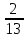 11. Для заданных векторов найти смешанное произведение [ 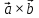 ] ]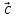 11.1. ( 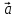 =1; -2; 1) =1; -2; 1) 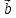 = (2; 1; -2) = (2; 1; -2) 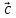 = (1; 1; 1) = (1; 1; 1)([ 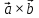 ] ]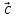 )= )=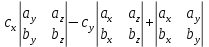 ([ 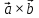 ] ]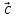 )=1 )=1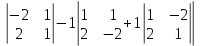 =1(-2-2)-1(-2-2)+1(1-(-4))= -4+4+5=5 =1(-2-2)-1(-2-2)+1(1-(-4))= -4+4+5=5Ответ: ([ 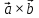 ] ]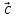 )=5 )=511.2. ( 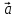 =1; 1; 2) =1; 1; 2) 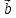 = (1; -1; 3) = (1; -1; 3) 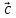 = (-2; -2; 1) = (-2; -2; 1)([ 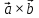 ] ]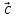 )=-2 )=-2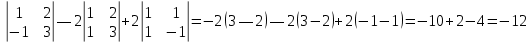 Ответ: ([ 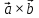 ] ]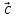 )=-12 )=-12 |
