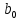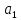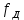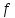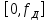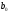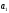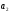2. Выполнение домашнего задания
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
111Equation Chapter 1 Section 11. Цель работы Провести экспериментальный анализ рекурсивных цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики фильтров, их взаимосвязь со значениями коэффициентов ЦФ; определить области устойчивости рекурсивных фильтров 1 и 2 порядка. 2. Выполнение домашнего задания 2.1 Исходные данные варианта Табл. 1. Таблица значений параметров фильтра
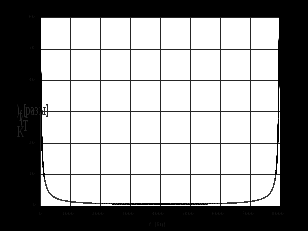
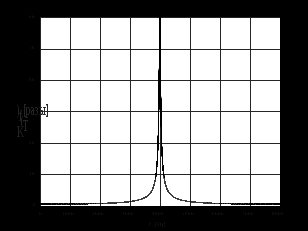
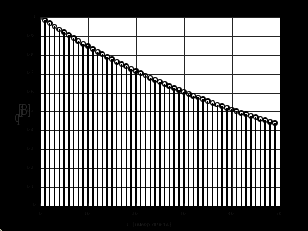
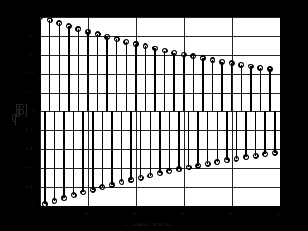
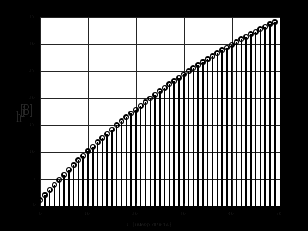
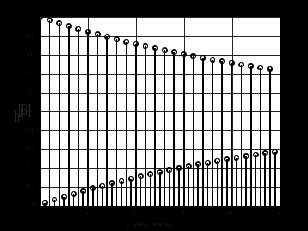
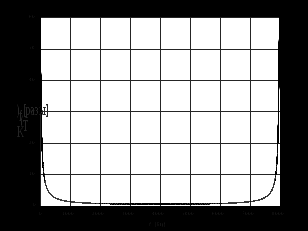
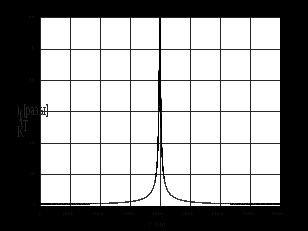
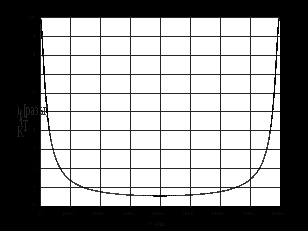
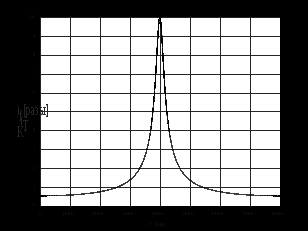
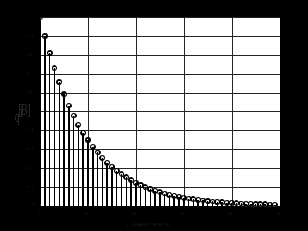
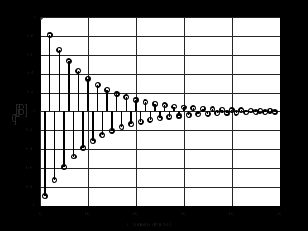
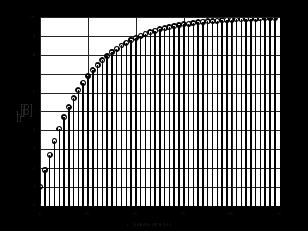
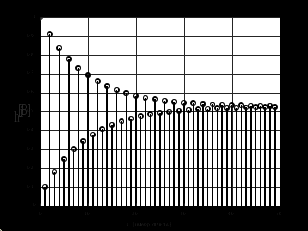
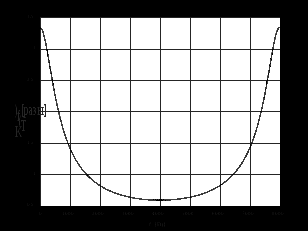
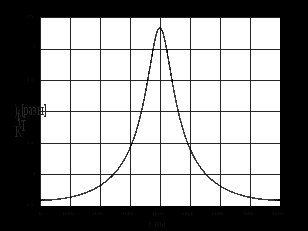
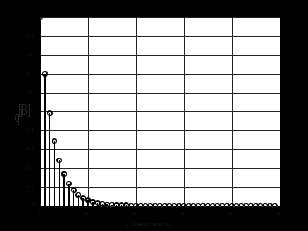
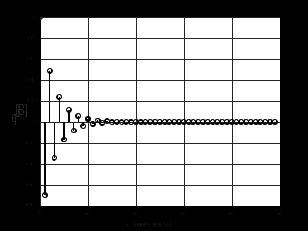
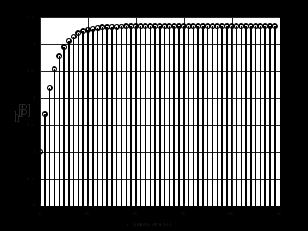
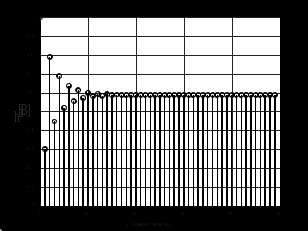
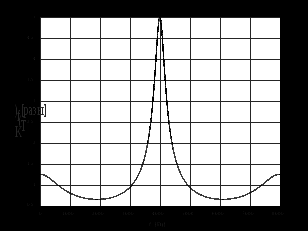
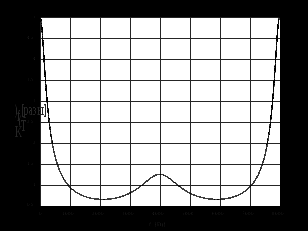
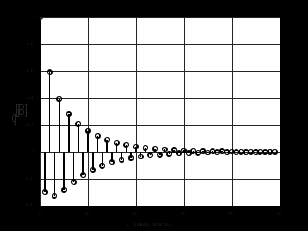
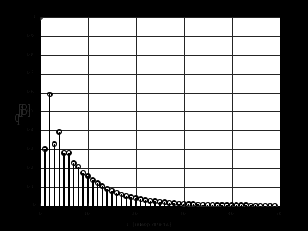
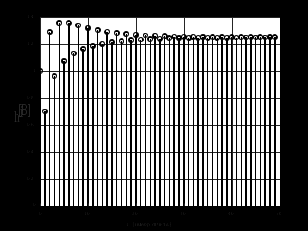
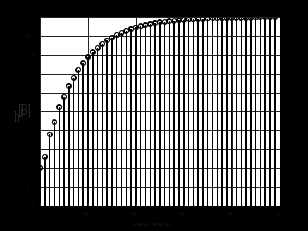
2.2 Запись разностного уравнения и системной функции Разностное уравнение рекурсивного ЦФ-1 (первого порядка) имеет вид: 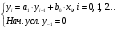 22\* MERGEFORMAT () 22\* MERGEFORMAT ()Построение системной функции 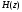 : :Пусть задан дискретный сигнал 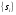 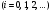 , тогда его односторонним , тогда его односторонним  - преобразованием называется: - преобразованием называется: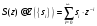 33\* MERGEFORMAT () 33\* MERGEFORMAT ()Свойства  - преобразования: - преобразования:Свойство 1 (линейности): 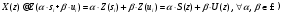 44\* MERGEFORMAT () 44\* MERGEFORMAT ()Свойство 2 (смещения): 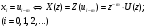 55\* MERGEFORMAT () 55\* MERGEFORMAT ()Пусть на входе ЦФ действует сигнал 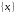 , а на его выходе наблюдается сигнал , а на его выходе наблюдается сигнал 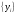 , тогда системной функцией ЦФ называется отношение: , тогда системной функцией ЦФ называется отношение: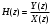 66\* MERGEFORMAT () 66\* MERGEFORMAT ()Находим 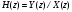 применив к обеим частям уравнения (1) Z преобразование и воспользовавшись свойствами линейности и смещения (свойство 1 и свойство 2): применив к обеим частям уравнения (1) Z преобразование и воспользовавшись свойствами линейности и смещения (свойство 1 и свойство 2):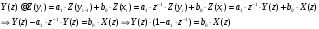 77\* MERGEFORMAT () 77\* MERGEFORMAT ()Отсюда получаем: 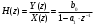 88\* MERGEFORMAT () 88\* MERGEFORMAT ()2.3 Структурная схема ЦФ Структурная схема цифрового фильтра строится на основе разностного уравнения (1). Ниже представлена структурная схема рекурсивного ЦФ 1-го порядка: 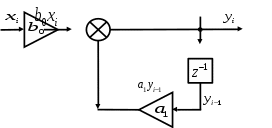 Рис. 1. Структурная схема рекурсивного ЦФ 1-го порядка ( 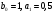 ) )2.4 Расчёт и построение импульсной реакции, переходной характеристики, амплитудно-частотной характеристики и фазо-частотной характеристики ЦФ Ниже представлена схема получения импульсной характеристики ЦФ:  Рис. 2. Схема получения ИХ По определению ИХ (см. рис. 2): 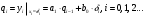 99\* MERGEFORMAT () 99\* MERGEFORMAT ()где 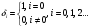 1010\* MERGEFORMAT () 1010\* MERGEFORMAT ()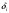 – единичный импульс Кронекера – единичный импульс Кронекера Из (8) с учётом начального условия и (9) последовательно получаем: 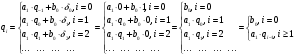 1111\* MERGEFORMAT () 1111\* MERGEFORMAT ()Ниже представлена импульсная характеристика ЦФ 1-го порядка: 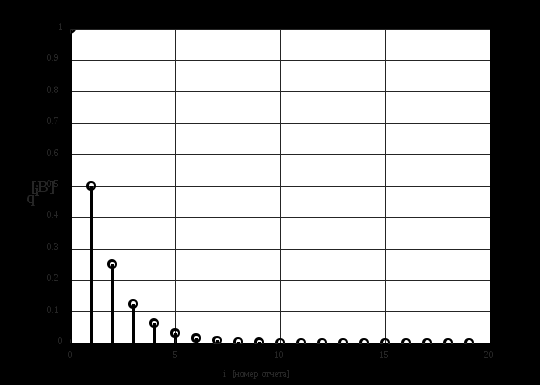 Рис. 3. Импульсная характеристика ЦФ 1-го порядка ( 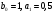 ) )Ниже представлена схема получения переходной характеристики ЦФ: 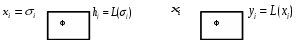 Рис. 4. Схема получения ПХ Переходной функцией 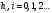 цифрового фильтра называется его отклик на дискретный единичный скачок: цифрового фильтра называется его отклик на дискретный единичный скачок: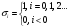 1212\* MERGEFORMAT () 1212\* MERGEFORMAT ()По определению фильтр называется устойчивым если при ограниченном входном воздействии 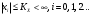 его выход (отклик) также ограничен, т.е. его выход (отклик) также ограничен, т.е. 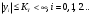 Следовательно, из определения выше следует, что для устойчивости ЦФ при действии на входе 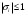 на выходе получаем на выходе получаем 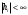 . .Из (11) следует, что: 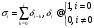 1313\* MERGEFORMAT () 1313\* MERGEFORMAT ()Любой ЦФ является дискретной линейной системой, действие которого на входной сигнал 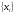 описывается линейным оператором описывается линейным оператором 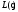 . Это означает, что выходной сигнал . Это означает, что выходной сигнал 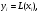 а если а если 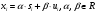 , то , то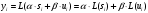 1414\* MERGEFORMAT () 1414\* MERGEFORMAT ()Выражение (13) описывает свойство линейности. Следовательно, если 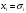 , то из (12) и (13) имеем: , то из (12) и (13) имеем: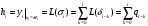 1515\* MERGEFORMAT () 1515\* MERGEFORMAT ()Делаем замену переменных 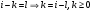 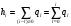 1616\* MERGEFORMAT () 1616\* MERGEFORMAT ()Из (15) c учётом (10) получаем: 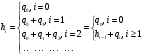 1717\* MERGEFORMAT () 1717\* MERGEFORMAT ()Отсюда получаем метод построения 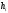 . Сначала, зная уравнение ЦФ строим ИХ . Сначала, зная уравнение ЦФ строим ИХ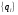 , затем по формуле (16) строим , затем по формуле (16) строим 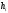 : :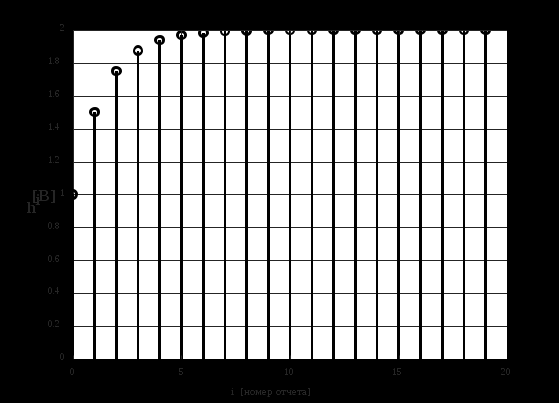 Рис. 5. Переходная характеристика ЦФ 1-го порядка ( 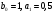 ) )Нахождение комплексного коэффициента передачи: Комплексным коэффициентом передачи ЦФ 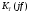 называется функция частоты называется функция частоты 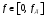 : :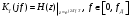 1818\* MERGEFORMAT () 1818\* MERGEFORMAT ()где 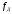 – частота дискретизации, – частота дискретизации, 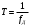 – интервал дискретизации – интервал дискретизацииСвойства комплексных чисел: Если 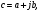 то то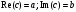 1919\* MERGEFORMAT () 1919\* MERGEFORMAT ()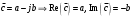 2020\* MERGEFORMAT () 2020\* MERGEFORMAT ()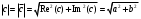 2121\* MERGEFORMAT () 2121\* MERGEFORMAT ()Если 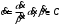 - комплексная дробь, то справедливо: - комплексная дробь, то справедливо: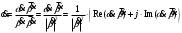 2222\* MERGEFORMAT () 2222\* MERGEFORMAT ()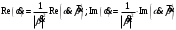 2323\* MERGEFORMAT () 2323\* MERGEFORMAT ()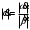 2424\* MERGEFORMAT () 2424\* MERGEFORMAT ()Формулы Эйлера: 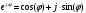 2525\* MERGEFORMAT () 2525\* MERGEFORMAT ()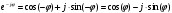 2626\* MERGEFORMAT () 2626\* MERGEFORMAT ()Находим 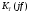 используя (17) и формулы Эйлера (24), (25): используя (17) и формулы Эйлера (24), (25):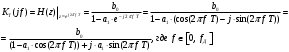 2727\* MERGEFORMAT () 2727\* MERGEFORMAT ()Находим Re и Im от 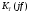 с учётом (21), (22), (23): с учётом (21), (22), (23):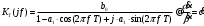 2828\* MERGEFORMAT () 2828\* MERGEFORMAT ()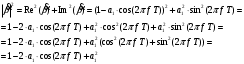 2929\* MERGEFORMAT () 2929\* MERGEFORMAT ()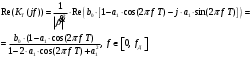 3030\* MERGEFORMAT () 3030\* MERGEFORMAT ()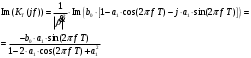 3131\* MERGEFORMAT () 3131\* MERGEFORMAT ()Нахождение АЧХ: Амплитудно-частотной характеристикой (АЧХ) ЦФ, называется функцией частоты: 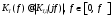 3232\* MERGEFORMAT () 3232\* MERGEFORMAT ()Находим АЧХ 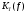 по формуле (31) и с учётом (23): по формуле (31) и с учётом (23):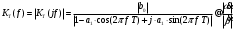 3333\* MERGEFORMAT () 3333\* MERGEFORMAT ()Преобразуем знаменатель с учётом полученного ранее 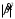 в формуле (28): в формуле (28):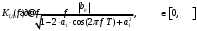 3434\* MERGEFORMAT () 3434\* MERGEFORMAT ()Ниже представлена амплитудно-частотная характеристика ЦФ 1-го порядка: 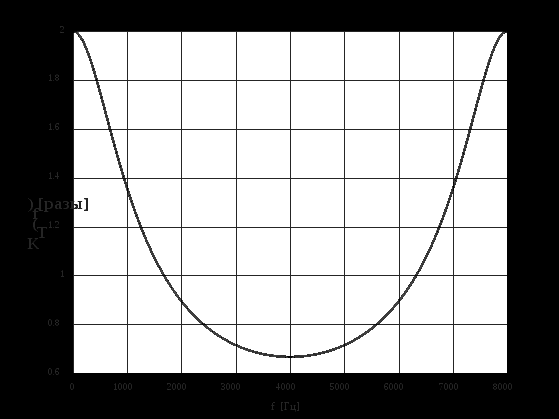 Рис. 6. АЧХ ЦФ 1-го порядка ( 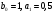 ) )Нахождение ФЧХ: Фазо-частотной характеристикой (ФЧХ) цифрового фильтра называется функция частоты: 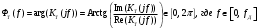 3535\* MERGEFORMAT () 3535\* MERGEFORMAT ()Находим ФЧХ 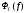 по формуле (34), используя (29), (30): по формуле (34), используя (29), (30):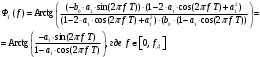 3636\* MERGEFORMAT () 3636\* MERGEFORMAT ()Ниже представлена фазо-частотная характеристика ЦФ 1-го порядка: 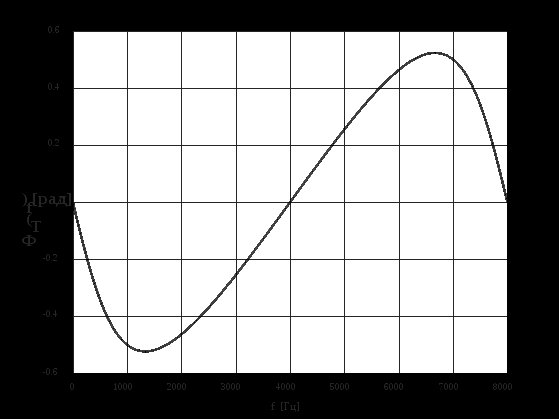 Рис. 7. ФЧХ ЦФ 1-го порядка ( 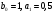 ) )3. Выполнение лабораторной работы 3.1. Исходные параметры фильтров Табл. 2. Таблица значений параметров исследуемых ЦФ 1-го и 2-го порядка
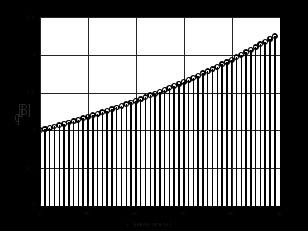
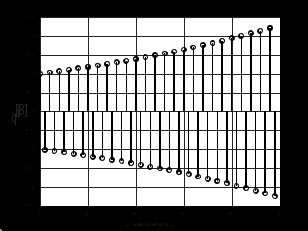
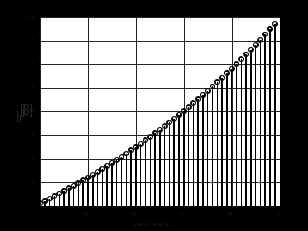
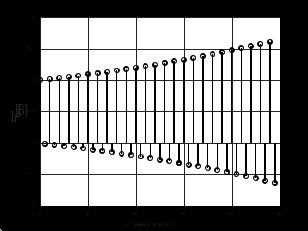
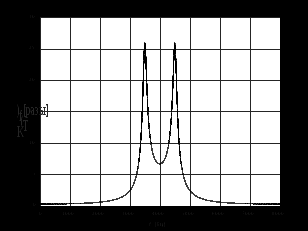
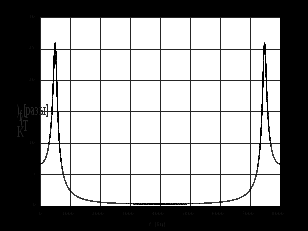
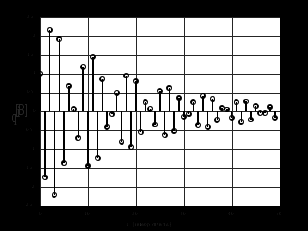
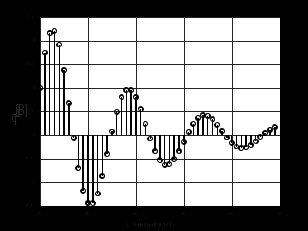
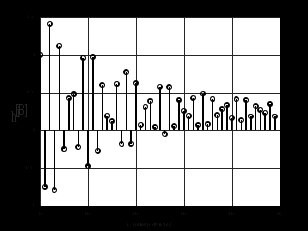
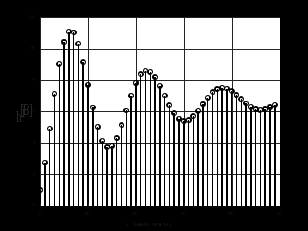
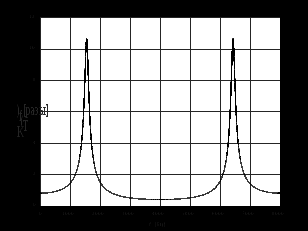
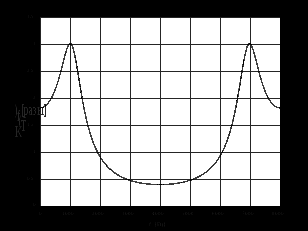
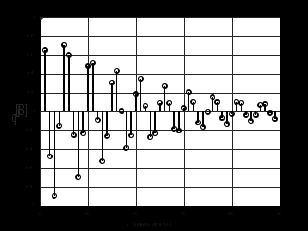
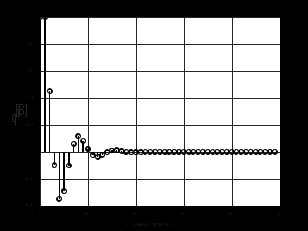
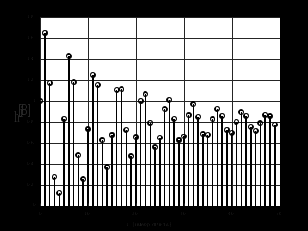
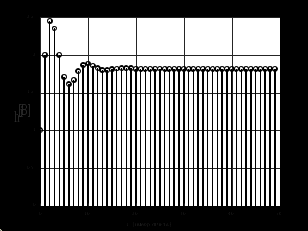
3.2. Структурные схемы исследуемых фильтров Разностное уравнение рекурсивного ЦФ-2 (второго порядка) имеет вид: 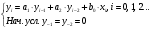 3737\* MERGEFORMAT () 3737\* MERGEFORMAT ()Структурная схема прямой реализации цифрового фильтра строится на основе разностного уравнения (36). Ниже представлена структурная схема рекурсивного ЦФ 2-го порядка: 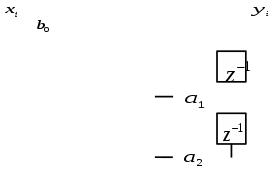 Рис. 8. Структурная схема прямой реализации рекурсивного ЦФ 2-го порядка Для составления канонической схемы цифрового фильтра второго порядка приведём его системную функцию. Находим 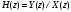 применив к обеим частям уравнения (36) Z - преобразование и воспользовавшись свойствами линейности и смещения (3), (4): применив к обеим частям уравнения (36) Z - преобразование и воспользовавшись свойствами линейности и смещения (3), (4):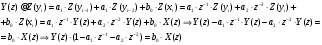 3838\* MERGEFORMAT () 3838\* MERGEFORMAT ()Отсюда и из (5) получаем: 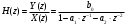 3939\* MERGEFORMAT () 3939\* MERGEFORMAT ()Введём вспомогательную функцию следующего вида: 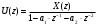 4040\* MERGEFORMAT () 4040\* MERGEFORMAT ()Откуда получаем следующее соотношение для 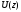 : :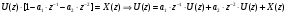 4141\* MERGEFORMAT () 4141\* MERGEFORMAT ()Теперь, с учётом (38) и выведенной функции 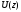 , для изображения отклика ЦФ имеем: , для изображения отклика ЦФ имеем: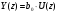 4242\* MERGEFORMAT () 4242\* MERGEFORMAT ()Пусть задано прямое Z – преобразование 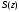 сигнала сигнала 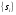 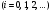 , тогда обратным , тогда обратным  - преобразованием называется: - преобразованием называется: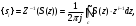 4343\* MERGEFORMAT () 4343\* MERGEFORMAT ()где  – контур, расположенный в области сходимости – контур, расположенный в области сходимости 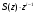 и охватывающий начало координат в z – плоскости (часто используют единичный контур с и охватывающий начало координат в z – плоскости (часто используют единичный контур с 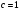 ). ).Применяя к (40) и (41) процедуру обратного Z-преобразования (42) и используя свойства Z-преобразования (3), (4), приходим к соотношениям для последовательностей 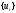 и и 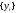 : :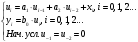 4444\* MERGEFORMAT () 4444\* MERGEFORMAT ()Каноническая структурная схема строится на основе уравнений (43). Ниже представлена структурная схема рекурсивного ЦФ 2-го порядка: 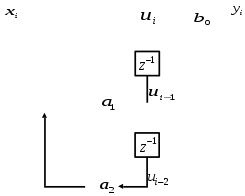 Рис. 9. Каноническая структурная схема рекурсивного ЦФ 2-го порядка 3.3. Результаты экспериментального исследования Ниже приведены формулы, по которым были рассчитаны характеристики ЦФ 1-го порядка. ИХ для ЦФ 1-го порядка находится по формуле (10). ПХ для ЦФ 1-го порядка находится по формуле (16). АЧХ для ЦФ 1-го порядка находится по формуле (33). Ниже приведены формулы, по которым были рассчитаны характеристики ЦФ 2-го порядка. По определению ИХ (см. рис. 2): 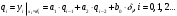 4545\* MERGEFORMAT () 4545\* MERGEFORMAT ()Из (44) с учётом начального условия и (36) последовательно получаем: 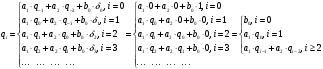 4646\* MERGEFORMAT () 4646\* MERGEFORMAT ()ПХ для ЦФ 2-го порядка находится по формуле (16).  Находим 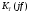 используя (17), (38) и формулы Эйлера (24), (25): используя (17), (38) и формулы Эйлера (24), (25):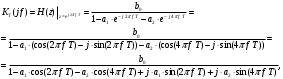 4747\* MERGEFORMAT () 4747\* MERGEFORMAT ()где 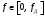 Находим Re и Im от 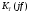 с учётом (21), (22), (23): с учётом (21), (22), (23):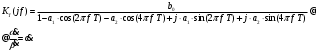 4848\* MERGEFORMAT () 4848\* MERGEFORMAT ()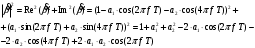 4949\* MERGEFORMAT () 4949\* MERGEFORMAT ()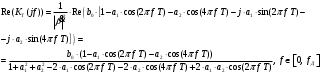 5050\* MERGEFORMAT () 5050\* MERGEFORMAT ()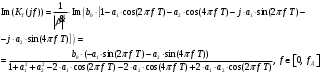 5151\* MERGEFORMAT () 5151\* MERGEFORMAT ()Находим АЧХ 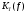 по формуле (31) с учётом (23) и полученного ранее по формуле (31) с учётом (23) и полученного ранее 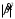 в формуле (48): в формуле (48):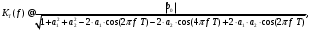 5252\* MERGEFORMAT () 5252\* MERGEFORMAT ()где 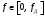 Ниже приведены графики АЧХ, ИХ и ПХ для исследуемых фильтров:
4. Детальные выводы по работе 4.1. Анализ устойчивости Рекурсивные цифровые фильтры первого и второго порядка называются устойчивыми, если их параметры 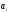 удовлетворяют следующим условиям: удовлетворяют следующим условиям: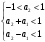 5353\* MERGEFORMAT () 5353\* MERGEFORMAT ()Также стоит отметить, что система является устойчивой, если выполняется требование затухания импульсной характеристики 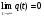 . .На основе приведённых выше критериев устойчивости можно сделать вывод, что неустойчивыми являются фильтр №5 и фильтр №6, а фильтр №1 и фильтр №2 находятся на границе устойчивости. Все остальные фильтры являются устойчивыми, так как для них выполняются приведённые выше условия (52) и их импульсная характеристика затухает. 4.2. Классификация фильтров Критерий классификации фильтров: Фильтр называется фильтром нижних частот (ФНЧ), если его АЧХ примыкает к нулевой частоте. Фильтр называется полосовым фильтром (ПФ), если его АЧХ локализована в середине рабочего диапазона. Фильтр называется фильтром верхних частот (ФВЧ), если его АЧХ примыкает к частоте Найквиста. На основе критерия выше произведём классификацию исследуемых фильтров: Сначала отметим фильтр №1 и фильтр №2, так как их параметры 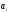 лежат на грани устойчивости. лежат на грани устойчивости.Фильтр №1: 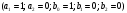 – ФНЧ 1-го порядка. – ФНЧ 1-го порядка.Фильтр №2: 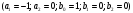 – ФВЧ 1-го порядка. – ФВЧ 1-го порядка.Фильтр №3: 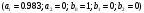 – ФНЧ 1-го порядка. – ФНЧ 1-го порядка.Фильтр №4: 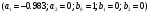 – ФВЧ 1-го порядка. – ФВЧ 1-го порядка.Фильтр №5: 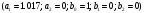 – ФНЧ 1-го порядка. – ФНЧ 1-го порядка.Фильтр №6: 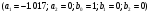 – ФВЧ 1-го порядка. – ФВЧ 1-го порядка.Фильтр №7: 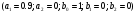 – ФНЧ 1-го порядка. – ФНЧ 1-го порядка.Фильтр №8: 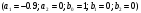 – ФВЧ 1-го порядка. – ФВЧ 1-го порядка.Фильтр №9: 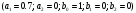 – ФНЧ 1-го порядка. – ФНЧ 1-го порядка.Фильтр №10: 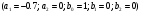 – ФВЧ 1-го порядка. – ФВЧ 1-го порядка.Фильтр №11: 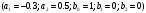 – ФВЧ 2-го порядка. – ФВЧ 2-го порядка.Фильтр №12: 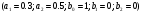 – ФНЧ 2-го порядка. – ФНЧ 2-го порядка.Фильтр №13: 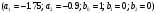 – ФВЧ 2-го порядка. – ФВЧ 2-го порядка.Фильтр №14: 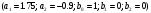 – ФНЧ 2-го порядка. – ФНЧ 2-го порядка.Фильтр №15: 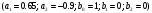 – ФНЧ 2-го порядка. – ФНЧ 2-го порядка.Фильтр №16: 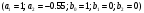 – ФНЧ 2-го порядка. – ФНЧ 2-го порядка.4.3. Анализ поведения АЧХ Проведём сравнение поведения АЧХ однотипных нерекурсивных (из лаб. 26-1) и устойчивых рекурсивных фильтров (из лаб. 26-2). Сравнивая нерекурсивный ФНЧ 1-го порядка (фильтр №1) и рекурсивные ФНЧ 1-го порядка (фильтр №3, фильтр №7, фильтр №9), а также нерекурсивный ФВЧ 1-го порядка (фильтр №2) и рекурсивные ФВЧ 1-го порядка (фильтр №4, фильтр №8, фильтр №10), видно, что рекурсивные фильтры обладают большей крутизной спада АЧХ от полосы пропускания к полосе подавления, как для ФНЧ 1-го порядка, так и для ФВЧ 1-го порядка, по сравнению с нерекурсивными фильтрами. Сравнивая нерекурсивные ФНЧ 2-го порядка (фильтр №3, фильтр №4) и рекурсивные ФНЧ 2-го порядка (фильтр №12, фильтр №14, фильтр №15, фильтр №16), видно, что у рекурсивных фильтров, в отличие от нерекурсивных, выше крутизна и пульсации вне полосы пропускания либо отсутствуют, либо меньше выражены, но появляются пульсации в полосе пропускания. Сравнивая нерекурсивные ФВЧ 2-го порядка (фильтр №5, фильтр №6) и рекурсивные ФВЧ 2-го порядка (фильтр №11, фильтр №13), видно, что рекурсивные фильтры обладают большей крутизной, большим уровнем пульсаций в полосе пропускания и меньшим уровнем пульсаций вне полосы пропускания. Проведём сравнение поведения АЧХ для однотипных рекурсивных фильтров первого и второго порядка. Сравнивая ФНЧ 1-го порядка (фильтр №3, фильтр №7, фильтр №9) и ФНЧ 2-го порядка (фильтр №12, фильтр №14, фильтр №15, фильтр №16), видно, что у ФНЧ 1-го порядка отсутствую пульсации как в полосе пропускания, так и вне её, а у ФНЧ 2-го порядка присутствуют пульсации в полосе пропускания и вне полосы пропускания. Сравнивая ФВЧ 1-го порядка (фильтр №4, фильтр №8, фильтр №10) и ФВЧ 2-го порядка (фильтр №11, фильтр №13), видно, что у ФВЧ 1-го порядка отсутствуют пульсации в полосе пропускания и вне полосы пропускания, а у ФВЧ 2-го порядка присутствуют пульсации в полосе пропускания и вне полосы пропускания. 4.4. Недостатки и преимущества исследуемых фильтров Преимущества рекурсивных фильтров заключаются в том, что для получения одних и тех же частотных характеристик, потребуется рекурсивный фильтр сильно меньшего порядка, нежели нерекурсивный, следовательно потребуется и меньшее количество элементов для его реализации. Основной недостаток рекурсивных фильтров заключается в том, что из-за наличия цепей обратной связи, их надо проверять на у |