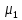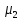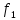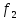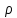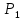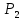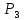12 Курманова Нураида АИСУк19-1 МиИОУ сро№2. 2 зіндік жмыс Пні Басару объектілерін моделдеу жне идентификациялау Таырыбы Бейсызыты модельдерді сызытандыру процедурасы Маманды 6B17108 Автоматтандыру жне басару Орындаан Курманова Н.
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Коммерциялық емес ашық акционерлік қоғам «Ғ. Ж. Дәукеев атындағы АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ» «Автоматтандыру және басқару» кафедрасы №2 Өзіндік жұмыс Пәні: «Басқару объектілерін моделдеу және идентификациялау» Тақырыбы: «Бейсызықты модельдерді сызықтандыру процедурасы» Мамандық: 6B17108 – «Автоматтандыру және басқару» Орындаған: Курманова Н.Н. Нұсқа: 12 Тобы: АИСУк-19-1 Тексерген: проф. Ибраева Л. К. _____________ ____________ «______» ____________________ 2022ж. (бағасы) (қолы) Алматы 2022 Жұмыс мақсаты: Объектінің бейсызықты модель теңдеуін сызықтандыру процедурасын оқу. 2.1 Негізгі сұрақтар: бейсызықты өрнектерді Тейлор қатарына жіктеу жолымен объект моделін сызықтандыру. 2.2 Әдістемелік кепілдемелер Әрқашан объектінің жүріс-тұрысын сызықты теңдеумен бейнелеу мүмкін емес. Осы себепке байланысты аргументтердің берілген диапазонында сызықты емес байланыстар сызықты өрнектермен аппроксимацияланады. Басқа сөзбен айтқанда кіріс аргументердің берілген диапазонында сызықты емес теңдеулерді сызықты теңдеулермен ауыстырамыз - теңдеулерді сызықтандырамыз. Сызықты объектілерде кіріс және шығыс сигналдардың байланыстарын беріліс функциямен жеңіл сипаттауға болады. Осындай идеалдау моделді құру процесін қарапайымдайды. Әдетте сызықты емес элементтерді сызықтандыру сигналдардың өздерінің стационарлы мәндерінен кіші шамаға ауытқулары бар деген шартта орындалады. Сызықты емес теңдеулерді сызықтандырудың негізінде келесідей болжам орнатылған: зерттелетін динамикалық процесте айнымалылар өзгергенде олардың орнықты мәндерінен ауытқулары әрқашан жеткілікті кіші шама болады. Динамикалық айнымалылардың кейбір орнықты мәндерінен ауытқулары кіші шамалар болу шарты әдетте автоматты реттеу жүйесі үшін орындалады. Бекітілген автоматты жүйенің жұмысының өзі осы шартты талап етеді. Сызықтандыру әдетте сызықты емес тәуелділіктерді Тейлор қатарына жіктеу жолымен орындалады; жіктеуді бастапқы стационар режим аймағында орындаймыз және жіктеудің тек қана сызықты мүшелерін қалдырып, соңынан алынған теңдеуден статика теңдеуін алып тастаймыз. Осы процедура көмегімен модель теңдеулері айнымалылары арқылы емес, олардың бастапқы стационар режимінен ауытқулары арқылы жазылады. Алынған теңдеуге Лаплас түрлендіруін қолданып объект моделін беріліс функциясы түрінде жеңіл жазуға мүмкіндік береді. Ұсынылып отырған өзіндік жұмыста №4 зертханалық жұмыста зерттелетін модельді сызықтандыру керек. Бұл жұмыста зерттеу объектісі резервуардағы сұйықтықтың қозғалу процесі болып табылады, оның моделін шығару үшін келесілер қолданылады: - зат массасының сақталу теңдеуі 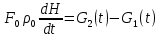 (2.1) (2.1)- кіріс ағыны үшін қозғалу заңы: 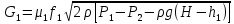 (2.2) (2.2)- шығыс ағыны үшін қозғалу заңы: 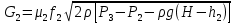 (2.3) (2.3)(2.2) және (2.3) теңдеулерді сызықтандыру үшін, оларды Тейлор қатарына жіктеп, сызықты мүшелерін қалдырамыз: 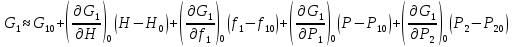 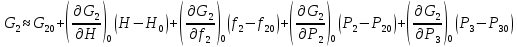 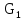 үшін жіктеудің коэффициенттерін табамыз (оларды үшін жіктеудің коэффициенттерін табамыз (оларды 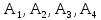 деп белгілейміз): деп белгілейміз):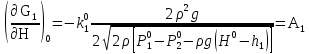 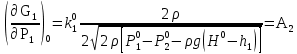 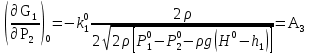 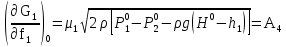 Сол сияқты 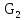 үшін жіктеудің коэффициенттерін табамыз (оларды үшін жіктеудің коэффициенттерін табамыз (оларды 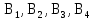 деп белгілейміз). деп белгілейміз).2.3 Тапсырмалар: 1. Зерттеу объектіні оқу, [2] әдебиеттегі, 26 б., 4.2 п. 2. Орнықталған күй аймағында бейсызықты өрнектерді Тейлор қатарына жіктеп, А1, А2, А3, А4, В1, В2, В3, В4 коэффициенттері үшін өрнектерін табыңыз. 3. MatLab Function блогын қолданып, осы коэффициенттерді есептеуге файл-функцияны құрыңыз (осы файл-функция модельдің блок-диаграммасын құру үшін №4 зертханалық жұмыста қолданылады). Коэффициенттердің есептелген мәндерін Display блогына шығарыңыз. 4. [2]-дегі модельдің соңғы түрін және Лаплас түрлендіруін қолданып, әртүрлі каналдар бойынша беріліс функцияларын алыңыз. Жұмыстың орындалу барысы: 1 кесте – Тапсырма нұсқалары
2. Орнықталған күй аймағында бейсызықты өрнектерді Тейлор қатарына жіктеп, А1, А2, А3, А4, В1, В2, В3, В4 коэффициенттері үшін өрнектерін табыңыз. 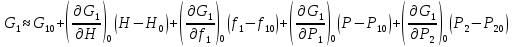 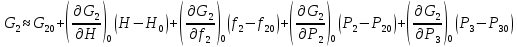 мұндағы «0» индексі орнықталған режимдегі айнымалылар мәндерін белгілейді. 𝐺1 үшін жіктеудің коэффициенттерін табамыз (оларды А1, А2, А3, А4 деп белгілейміз): 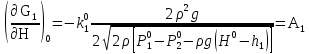 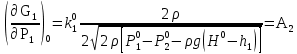 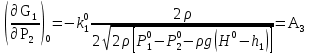 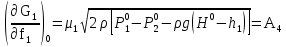 Сол сияқты 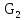 үшін жіктеудің коэффициенттерін табамыз (оларды үшін жіктеудің коэффициенттерін табамыз (оларды 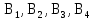 деп белгілейміз). деп белгілейміз).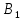 коэффициентінің өрнегін туынды бойынша табамыз: коэффициентінің өрнегін туынды бойынша табамыз: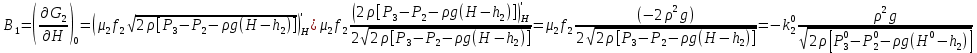 ; ;Осыдан 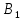 коэффициентінің өрнегі: коэффициентінің өрнегі: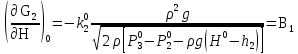 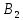 коэффициентінің өрнегін туынды бойынша табамыз: коэффициентінің өрнегін туынды бойынша табамыз: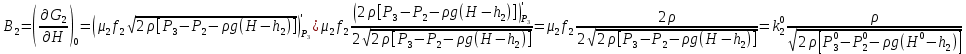 ; ;Осыдан 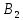 коэффициентінің өрнегі: коэффициентінің өрнегі: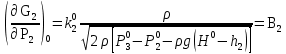 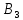 коэффициентінің өрнегін туынды бойынша табамыз: коэффициентінің өрнегін туынды бойынша табамыз: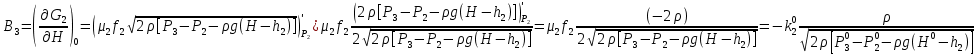 ; ;Осыдан 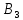 коэффициентінің өрнегі: коэффициентінің өрнегі: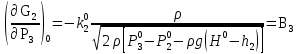 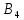 коэффициентінің өрнегін туынды бойынша табамыз: коэффициентінің өрнегін туынды бойынша табамыз: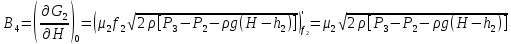 ; ;Осыдан 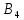 коэффициентінің өрнегі: коэффициентінің өрнегі: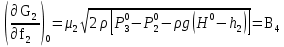 3. MatLab Function блогын қолданып, осы коэффициенттерді есептеуге файл-функцияны құрыңыз (осы файл-функция модельдің блок-диаграммасын құру үшін №4 зертханалық жұмыста қолданылады). (2.1), (2.2), (2.3) теңдеулерден процесс динамикасын сипаттайтын модельдің дифференциалды теңдеуін аламыз: 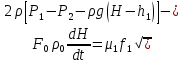 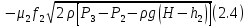 Кірістегі айнымалылар ретінде 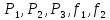 айнымалыларын таңдаймыз. Сиымдылықтағы процестің сызықты моделін алу керек. Жүйенің бастапқы тепе-теңдің күйі айнымалыларын таңдаймыз. Сиымдылықтағы процестің сызықты моделін алу керек. Жүйенің бастапқы тепе-теңдің күйі 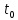 уақытында деп есептейміз. уақытында деп есептейміз.Бастапқы тепе-теңдік күйдегі процестің күй координаталарының мәндерін бағалау үшін статикалық модельді табамыз. Тепе-теңдің күйде келесі шарт орындалады: 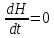 Берілген (2.1) теңдеуден: 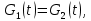 яғни яғни 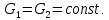 Осыдан: 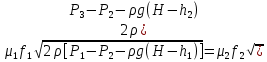 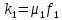 және және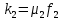 деп белгілейміз. Алдыңғы теңдіктен Н үшін өрнекті табамыз. Осыдан, статикалық модельді аламыз: деп белгілейміз. Алдыңғы теңдіктен Н үшін өрнекті табамыз. Осыдан, статикалық модельді аламыз: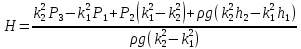 (2.5) (2.5)Алдымен matlab-ты қосып Simulink пакетін ашып, сосын User Defined Functions-ты Library-дан іздеп Simulink ортасына қоямыз, үстін екі рет шерткенде бізге matlab функциясына апарады және соның ішіне біз өзімізге қажетті формуланы жазамыз (1 сурет). Бұл жерде k1 мен k2-ні есептеп аламыз. Функция ішіне кодты жазып болған соң Simulink-те функцияның кіріс және шығыстарын орнатамыз, кіріс шамаларын constant-тармен белгілеп, екі шығысты Mux-қа жалғап дисплейден шыққан мәндерді көреміз (2 сурет). 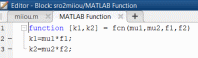 1 Сурет – k1 мен k2 функция коды 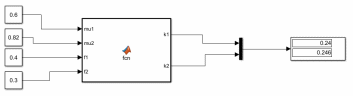 2 Сурет – Simulink-тегі сұлбасы 2 Сурет – Simulink-тегі сұлбасы Келесіде Н-ты табамыз (2.5 формула), ол үшін Matlab функцияны ашып кодтарды тереміз қажет айнымалыларды белгілейміз табу керек айнымалыға меншіктейміз, формуласын жазып Simulink ортасында кіріс мәндерімен шығысын орнатамыз. (3 сурет)  3 Сурет – Н функциясының коды 3 Сурет – Н функциясының коды 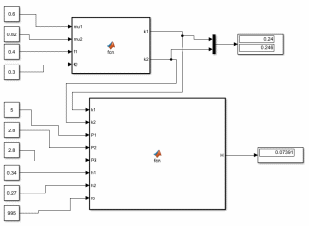 4 Сурет – Simulink-тегі сұлбасы А1, А2, А3, А4, В1, В2, В3, В4 мәндерін табамыз, ол үшін 1 тапсырмадағы есептелген формулаларды пайдаланамыз жоғарыда айтылған мұнда да дәл солай функцияның айнымалыларын енгіземіз және формуланы жазамыз. 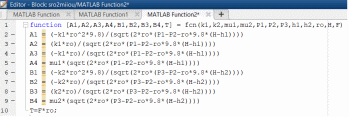 5 Сурет – Функцияның коды 5 Сурет – Функцияның кодыSimulink ортасында кіріс айнымалылары ретінде нұсқа бойынша сан мәндерін аламыз және k1, k2 және H мәндерін алдындағы есептелген бойынша кіріс айнымалы ретінде жалғаймыз. 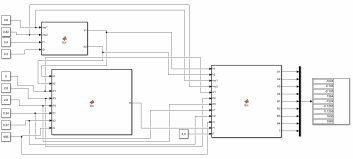 6 Сурет – Simulink-тегі сұлбасы 6 Сурет – Simulink-тегі сұлбасы4. [2]-дегі модельдің соңғы түрін және Лаплас түрлендіруін қолданып, әртүрлі каналдар бойынша беріліс функцияларын алыңыз. 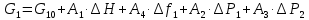 ; ;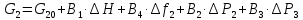 ; ;(2.4) теңдеуді сызықтандыру нәтижесінде алынған сызықты динамикалық модель келесі түрде болады: 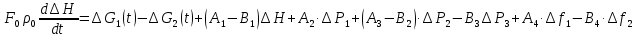 Жазуды қысқарту үшін келесідей белгілеулерді қолданамыз: 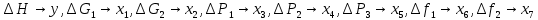 Сызықты модельдің соңғы түрі: 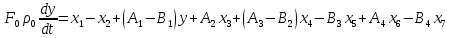 Беріліс функцияға көшу үшін 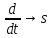 Лаплас операторын қолданып, кіріс және шығыс сигналдарының Лаплас түріндегі бейнесіналып (мысалы Лаплас операторын қолданып, кіріс және шығыс сигналдарының Лаплас түріндегі бейнесіналып (мысалы 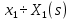 ) және ) және 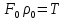 (F = 3,4 №3 зертханалық жұмыс бойынша) деп белгілеп, келесі түрде аламыз: (F = 3,4 №3 зертханалық жұмыс бойынша) деп белгілеп, келесі түрде аламыз: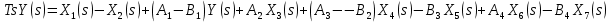 . .Осы алгебралық теңдеуден әртүрлі каналдар бойынша беріліс функцияларын анықтаймыз: 1-ші канал бойынша беріліс функциясын табамыз, ол үшін біз алдымен теңдеуді ықшамдаймыз: 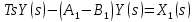 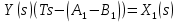 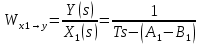 Сан мәндерін қойғанда: 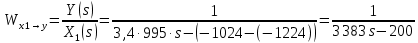 2-ші канал бойынша беріліс функциясын табамыз: 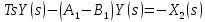 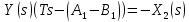 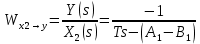 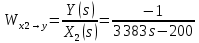 3-ші канал бойынша беріліс функциясын табамыз оны табу дәл бірінші және екінші беріліс функцияларын тапқанмен бірдей, тек кірудегі сигнал мәні өзгереді: 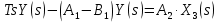 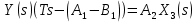 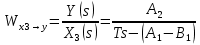 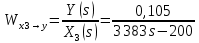 4-ші канал бойынша беріліс функциясын табамыз: 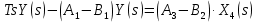 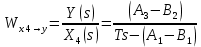 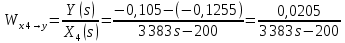 5-ші канал бойынша беріліс функциясын табамыз: 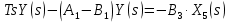 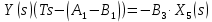 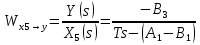 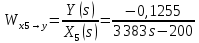 6-ші канал бойынша беріліс функциясын табамыз: 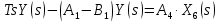 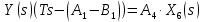 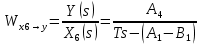 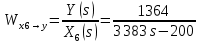 7-ші канал бойынша беріліс функциясын табамыз: 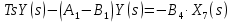 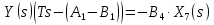 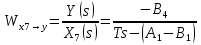 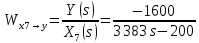 Қорытынды Өзіндік жұмысты орындау барысында объектінің бейсызықты модель теңдеуін сызықтандыру процедурасы үйретілді. Орнықталған күй аймағында бейсызықты өрнектерді Тейлор қатарына жіктеп, А1, А2, А3, А4, В1, В2, В3, В4 коэффициенттері үшін өрнектері табылды. Одан кейін MatLab Function блогы қолданылып, осы коэффициенттерді есептеуге файл-функция құрылды. Коэффициенттердің есептелген мәндері Display блогына шығарылды. [2]-дегі модельдің соңғы түрін және Лаплас түрлендіруі қолданылып, әртүрлі каналдар бойынша беріліс функциялары алынды. |