20 г гелия, заключенного в цилиндре под поршнем, очень медленно переводят из состояния 1
 Скачать 46.5 Kb.
|
|
78. 20 г гелия, заключенного в цилиндре под поршнем, очень медленно переводят из состояния 1 (p1 = 4,1 атм., V1 = 32 л) в состояние II (p2 = 15,5 атм., V2 = 9 л). Какой наибольшей температуры достигает газ при этом процессе, если график зависимости давления от объема – прямая линия (рисунок)? Н  анесем на график сетку изотерм – гипербол  .Чем выше температура газа, тем дальше находится вершина гиперболы от начала координат. Поэтому ясно, что во время процесса I – II газ достигает наибольшей температуры, при которой соответствующая гипербола не пересекает прямую I – II, а только касается ее. Так как точка с координатами p и V, соответствующая максимальной температуре, лежит как на гиперболе, так и на прямой, то ее координаты должны удовлетворять двум уравнениям: уравнению гиперболы  и уравнению прямой  ( и – постоянные). Их мы определим позже. Подставляя p из второго уравнения в первое, получим квадратное уравнение для V:  .Так как гипербола и прямая должны иметь лишь одну общую точку, то это уравнение может иметь только один корень, то есть его дискриминант должен быть равен нулю:  .Решая последнее уравнение относительно T, найдем  .В это выражение нужно подставить значения коэффициентов и . Так как точки I и II принадлежат одной и той же прямой  .Решая эту систему уравнений, найдем  .Поэтому 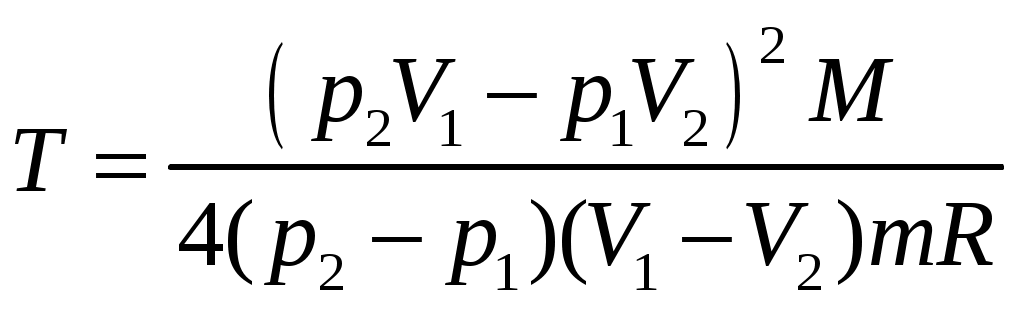 .Подставив численные значения входящих в это выражение величин, получим  . |