2021 РТ2 вариант1 без ответов. 2021г. Рт2 (вариант 1) Часть a в заданиях А12 и А16 может быть два и более правильных ответа, в остальных один правильный ответ
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
2021г. РТ2 (вариант 1) Часть A В заданиях А12 и А16 может быть два и более правильных ответа, в остальных – один правильный ответ.
А2. Среди чисел 1) А3. Среди данных чисел укажите номер нечетного числа, если известно, что число 1) 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. А4. Среди чисел 1) 1; 2) 2; 3) 3; 4) 4; 5) 5.
А6. Значение выражения  равно: равно:1) –1; 2) –2; 3) 0; 4) 1; 5) 2.
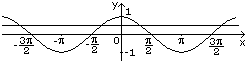
A9. Укажите номер верного утверждения для любых чисел 1) 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. A10. Абсцисса точки пересечения графика функции 1) 7; 2) 5; 3) 44; 4) 54; 5) 12. A11. Укажите номер системы уравнений, которая не имеет решений. 1) 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. A12. Функции заданы графиками на рисунках 1–5. Укажите номера рисунков, на которых изображен график функции, которая не является ни четной, ни нечетной. 1) 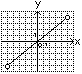 2) 2) 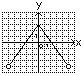 3) 3) 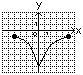 4) 4) 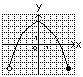 5) 5) 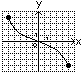 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. А13. Результат разложения многочлена 1) A14. Найдите натуральное число 1) 165; 2) 234; 3) 57; 4) 81; 5) 1431. A15. Из точки 1) A16. Для неравенства 1) Неравенство равносильно неравенству 2) неравенство верно при 3) неравенство равносильно неравенству 4) неравенство верно при 5) неравенство равносильно неравенству 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. A17. Найдите сумму всех натуральных значений 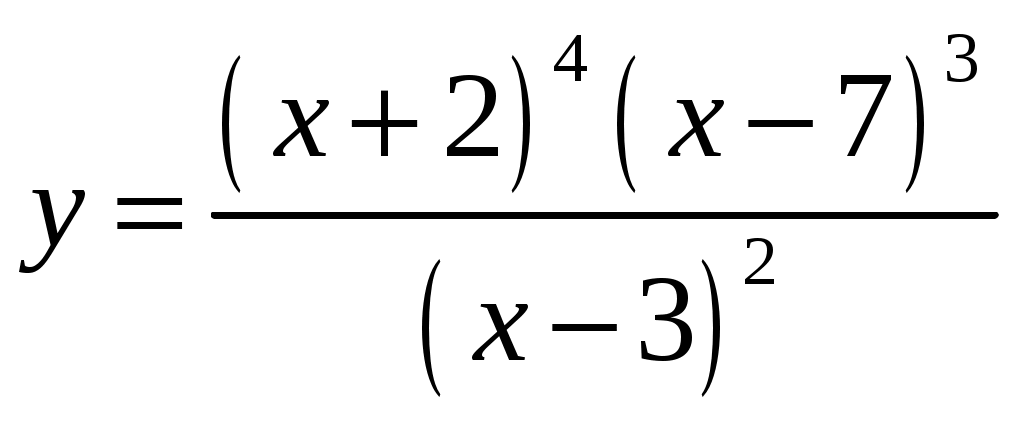 принимает неположительные значения. принимает неположительные значения.1) 25; 2) 22; 3) 12; 4) 42; 5) 27
Часть B B1. Для начала каждого из предложений А–В подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.
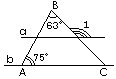
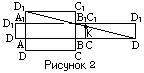
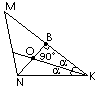
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4 B2. На рисунке изображен тупоугольный равнобедренный треугольник
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 235. B3. Для начала каждого из предложений А–В подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.
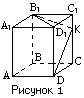
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4 B4. Имеются три бочки общей вместимостью 132 л. Если первую бочку наполнить целиком водой, а затем перелить ее в две другие, то либо третья бочка будет полной, а вторая заполненной наполовину, либо вторая будет полной, а третья заполнится на треть. Найдите объем (в литрах) большей из бочек. B5. Определите наименьшее количество членов арифметической прогрессии 4, 6, 8, …, которые нужно взять (начиная с первого), чтобы их сумма была больше 180. B6. Найдите значение выражения 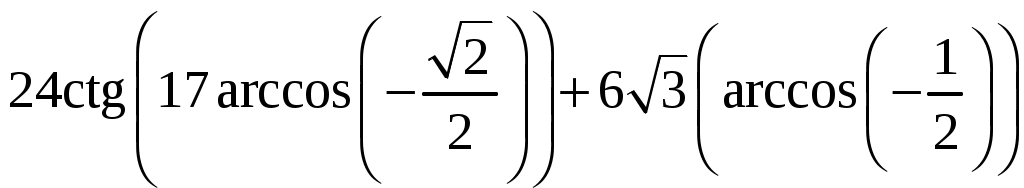 . .B7. В прямоугольном треугольнике B8. Найдите (в градусах) сумму корней уравнения B9. Сечением куба плоскостью является правильный шестиугольник, площадь которого равна B10. Найдите произведение наибольшего целого решения на количество всех целых решений неравенства B11. На сторонах B12. Решите уравнение B13. Бригада каменщиков одинаковой квалификации за рабочий день выложила кирпичную стену. Работу начал один каменщик. Остальные члены бригады присоединялись к нему по одному через равные промежутки времени. В тот момент, когда в работу включился последний каменщик, была выложена B14. Два одинаковых шара радиуса 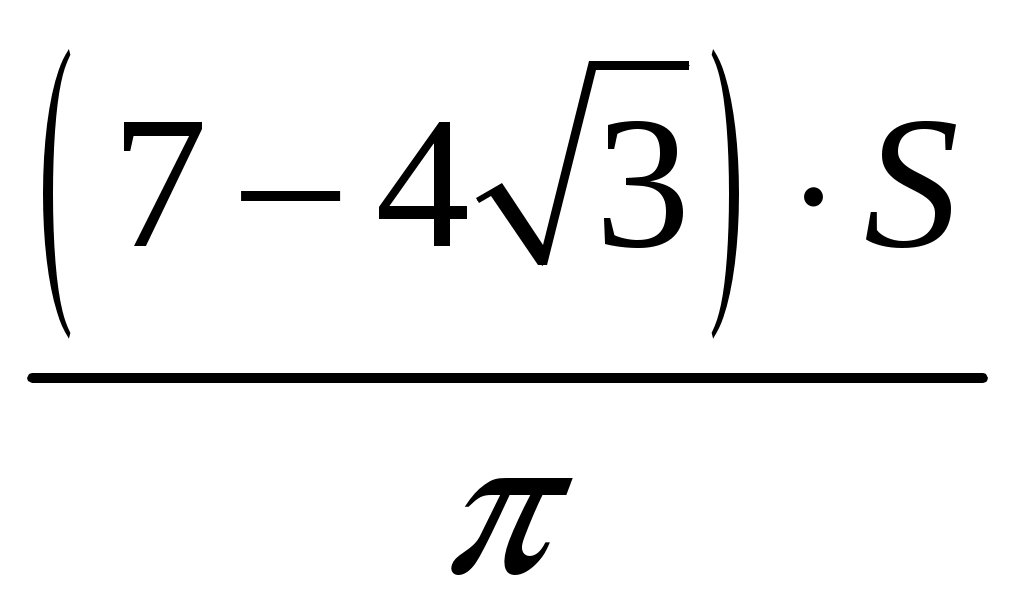 . . |