шпоры 21-30 (29, 30 не нашел). 21. Анализ цикла поршневого двс со смешанным подводом теплоты

• Название: 21. Анализ цикла поршневого двс со смешанным подводом теплоты
• Дата: 09.03.2023
• Размер: 419 Kb.
• Имя файла: шпоры 21-30 (29, 30 не нашел).doc
• Тип: Документы; #976902

21. Анализ цикла поршневого двс со смешанным подводом теплоты. В ДВС с воспламенением рабочей смеси (около ВМТ) от электрической искры время сгорания очень мало, в связи, с чем допустимо принять, что процесс подвода теплоты осуществляется при постоянном объеме (процесс 3 – 2 и процесс 5 – 1). В рассматриваемом цикле степень предварительного расширения ρ равна единице.



Таким образом, термический КПД цикла с подводом теплоты при постоянном объеме зависит от свойств рабочего тела и конструкции двигателя. Это иллюстрируется графиком (приложение 2), который показывает, что термический КПД двигателя увеличивается по мере увеличения степени сжатия ε.

Нагрузка на двигатель в термодинамическом цикле характеризуется количеством теплоты, подводимый к рабочему телу от горячего источника. Для цикла с подводом теплоты при постоянном объеме(V=const).

Следовательно, нагрузка при заданных значениях С_v и Т₂ пропорциональна степени повышения давления λ и не зависит от степени сжатия ε. Это свидетельствует о том, что термический КПД при изменении нагрузки не меняется.

Показывает, что с увеличением количества подведенной теплоты (степень повышения давления λ) среднее давление цикла ρ также увеличивается.

В цилиндрах двигателей внутреннего сгорания с воспламенением от сжатия при такте сжатия сжимается чистый воздух. Вблизи от ВМТ в цилиндр двигателя через форсунку впрыскивается распыленное топливо, которое в среде горячего воздуха самовоспламеняется и сгорает.

Процесс подвода теплоты к рабочему телу принимается в этом случае изобарным (Р=const).
η_t=1-1/(ε^k-1)*(λ*ρ^k-1)/(λ-1+k*λ*(ρ-1)).
Данная формула показывает, что термический КПД рассматриваемого цикла увеличивается при возрастании степени сжатия ε (приложение 2) и уменьшается при возрастании степени предварительного расширения ρ (приложение 2).

При увеличении нагрузки двигателя, то есть при увеличении количества подведенной теплоты, увеличивается степень предварительного расширения ρ и не изменяется степень сжатия. Следовательно, по мере увеличения нагрузки двигателя термический КПД цикла при постоянном давлении уменьшается (приложение 2). Это подтверждается sT – диаграммой (приложение 1), показывающей, что по мере увеличения подвода теплоты выигрыш в работе цикла от дополнительных количеств теплоты постепенно уменьшается.

22. Эксергия Теплоты Максимальную полезную работу (работоспособность) в совре-

менной термодинамике принято называть э к с е р г и е й 1)

. В данном случае вели-

чина — это эксергия источника работы, находящегося в объеме V; будем

обозначать эту величину EV. Таким образом,

EV= (U – U0) – T0(S – S0) -p0(V0 – V).

Э к с е р г и е й т е п л о т ы , отбираемой от горячего источника с температурой T1, называют ту максимальную полезную работу, которая может быть получена за счет этой теплоты при условии, что холодным источником теплоты служит

окружающая среда с температурой T0. Условимся в дальнейшем обозначать

эксергию теплоты Eq.

Чем больше разность температур между горячим и холодным

источниками, тем бóльшая доля теплоты, отбираемой от горячего источника,

может быть превращена в работу в цикле.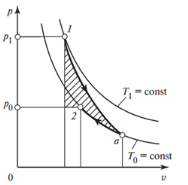






Необходимо отчетливо представлять себе, что поскольку рабочее тело совер-

шает замкнутый процесс, то его внутренняя энергия в результате совершения

цикла не изменяется и поэтому работа может быть произведена только за счет

теплоты Q1, сообщаемой рабочему телу горячим источником. Важно отметить,

что эксергия теплоты не зависит от давления среды p0, так как объем рабочего тела в результате совершенного им кругового процесса остается неизменным, окружающая среда не подвергается в итоге сжатию или расширению и вся работа, произведенная рабочим телом за цикл, может быть использована по нашему усмотрению, т.е. является полезной. Доля теплоты Q1, превращенной в работу в цикле, тем больше, чем выше термический КПД цикла. Как показано ранее, в заданном интервале температур наибольший термический КПД имеет обратимый цикл Карно. Следовательно, максимальная

полезная работа некоторого количества теплоты Q1, отбираемой от горячего

источника с температурой T1, будет получена в том случае, когда в рассматриваемой системе осуществляется обратимый цикл Карно.

Отсюда следует:

где — термический КПД обратимого цикла Карно, осуществляемого в

интервале температур T1—T0.

Как видно из этого уравнения, эксергия (работоспособность) теплоты Еq

тем

больше, чем меньше отношение T0/ T1. Если температуры источников теплоты

равны между собой (T0= T1), то эксергия теплоты в этом случае равна нулю.

Если между двумя рассматриваемыми источниками теплоты осуществляется

необратимый цикл, то полезная работа теплоты, отбираемой от горячего источ-

ника, меньше, чем эксергия (работоспособность) теплоты, поскольку термиче-

ский КПД любого необратимого цикла, как помнит читатель, всегда меньше

термического КПД обратимого цикла Карно.

23. Анализ цикла ГТУ с изобарным подводом теплоты.

В качестве простейших циклов газотурбинных установок (ГТУ) приняты: цикл с изобарным подводом теплоты и цикл с изохорным подводом теплоты. Эти циклы отличаются от соответствующих циклов д. в. с. процессом отвода теплоты — изохорный процесс отвода заменен изобарным. Современные ГТУ в основном работают с изобарным подводом теплоты.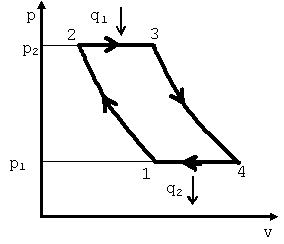


Рис. 7.6. Цикл ГТУ с изобарным подводом теплоты

Теоретический цикл ГТУ с изобарным подводом теплоты (рис. 7.6) состоит из процесса адиабатного сжатия воздуха 1—2 в компрессоре, процесса изобарного подвода теплоты 2—3 в камере сгорания и процесса адиабатного расширения 3—4 продуктов сгорания в соплах газовой турбины. После преобразования кинетической энергии струи газа на рабочих лопатках и процесса отвода теплоты 4—1 от газа в окружающую среду при постоянном давлении р1 цикл завершается.

Полезная работа в цикле равна разности между технической работой турбины и технической работой, затраченной на привод компрессора.

Полезная работа в цикле равна разности между технической работой турбины и технической работой, затраченной на привод компрессора.

Цикл газовой турбины с изобарным подводом теплоты характеризуется степенью повышения давления в цикле .

Можно показать, что .

То есть термический к. п. д. цикла ГТУ с подводом тепла при p=const увеличивается с увеличением степени повышения давления.

24. Теплофикационные циклы с турбинами с отбором пара.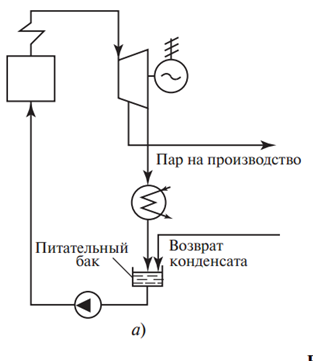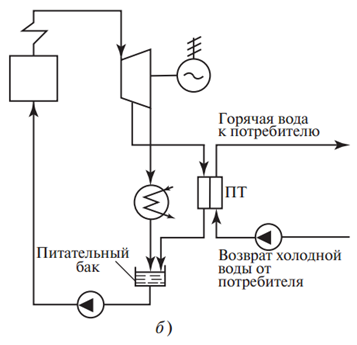





На рис. 11.40 показана схема ТЭЦ с турбинами с отбором пара. В этой схеме

часть пара достаточно высоких параметров отбирается из промежуточных ступе-

ней турбины (с этой точки зрения эта схема напоминает схему установки с реге-

неративными подогревателями). Отобранный пар может быть либо направлен на

производство (так называемый производственный отбор), откуда в установку воз-

вращается конденсат (рис. 11.40, а), либо в специальные подогреватели-теплооб-

менники (ПТ), в которых этот пар нагревает воду, используемую для отопитель-

ных целей (так называемый теплофикационный отбор, рис. 11.40, б). Следует

заметить, что на современных ТЭЦ наиболее распространены турбины с отбо-

ром пара.

Для характеристики экономичности работы ТЭЦ применяется так называемый

коэффициент использования теплоты K, определяемый как отношение суммы

полезной работы, произведенной в цикле, lэ

и теплоты q2, отданной внешнему

потребителю, к количеству теплоты q1, выделившейся при сгорании топлива:

или, что то же самое,



где N — электрическая мощность установки; В — часовой расход топлива;

— теплота сгорания топлива; Q — количество теплоты, отданной внешнему потребителю (за 1 час).

Значение K тем ближе к единице, чем совершеннее установка, т.е. чем

меньше потери теплоты в котлоагрегате и паропроводе, механические потери в

турбине, механическиe и электрические потери в электрогенераторе.

25. Анализ цикла ГТУ с ихохорным подводм теплот.



Теоретический цикл ГТУ с изохорным подводом теплоты (рис. 7.7) состоит из процесса адиабатного сжатия воздуха 1—2 в компрессоре, процесса изохорного подвода теплоты 2—3 в камере сгорания и процесса адиабатного расширения 3—4 продуктов сгорания в соплах газовой турбины. После преобразования кинетической энергии струи газа на рабочих лопатках и процесса отвода теплоты 4—1 от газа в окружающую среду при постоянном давлении р1 цикл завершается.

Цикл газовой турбины с изохорным подводом теплоты характеризуется степенью повышения давления при сжатии и степенью повышения давления при подводе теплоты .

Можно показать, что

Исследование последнего выражения показывает, что термический к. п. д. ГТУ с изохорным подводом теплоты возрастает с увеличением β и λ.

Цикл ГТУ с подводом теплоты при v=const не получил широкого распространения из-за сложности конструкции камеры сгорания и ухудшения условий работы турбины в пульсирующем потоке продуктов сгорания.

26. Эксергетический анализ циклов.

Рассмотрим неизолированную систему, состоящую из источника

работы, представляющего собой поток рабочего тела с давлением p1 и температурой T1 и окружающей среды (ее параметры p0 и T0). Подсчитаем максимальную

полезную работу (т.е. работоспособность) источника работы в такой системе

в расчете на единицу массы рабочего тела. Максимальная полезная работа производится

системой, в которой отсутствует равновесие, в том случае, если процессы, веду-

щие к установлению равновесия, осуществляются обратимо. Если источник

работы имеет температуру T1 и давление p1, а среда — T0 и p0 (Т, s-диаграмма

на рис. 9.2),



то этот источник работы может быть

обратимо переведен в состояние равновесия с

окружающей средой, например, следующим путем.

Вначале осуществляется обратимый адиабатный

процесс, в результате которого температура источ-

ника работы снижается от Т1 до T0, а давление- от p1 до pa; затем осуществляется изотермический процесс, в котором за счет теплообмена со средой источник работы достигает давления р0 (этот изо-

термический процесс обратим, поскольку температуры источника работы и среды в этом процессе одинаковы и равны T0 и, следовательно, процесс теплообмена происходит при бесконечно малой разности температур, т.е. обратим). Любой другой процесс (или комбинация процессов) между состояниями 1 и 0 был бы необра-

тим. В самом деле, любой другой процесс связан с отводом теплоты от источника работы, но, поскольку исходная температура источника работы Т1 отлична от температуры окружающей среды Т0, такой отвод теплоты будет необратимым.

Работа, совершаемая потоком в обратимом адиабатном процессе 1-а, равна:



Напомним, что эта разность энтальпий превращается в кинетическую энергию потока, которая затем легко может быть превращена в различные виды работы; в соответствии с уравнением первого закона термодинамики для потока



в адиабатном процессе (q = 0)



Работа, совершаемая потоком в обратимом изотермическом процессе а-0,

определяется следующим соотношением, которое вытекает из уравнения:



где qа-0 — теплота, отводимая от источника работы (потока) в этом изотермическом процессе. В соответствии с уравнением



и, следовательно,



Работа, совершаемая потоком в результате обратимого перехода из состояния 1 в состояние 0, равна сумме работ в обратимых процессах 1-а и а-0



имея в виду, что s1= sа, получаем:



Поскольку работа процесса обратимого изменения состояния источника работы представляет собой максимальную полезную работу (работоспособность) потока, можно записать:

Удельную работоспособность потока называют его эксергией. Эксергию

потока (для единицы массы) обозначают е:

e = (h – h0) + T0(s0– s)

Из этого уравнения следует, что эксергия потока однозначно определена,

если заданы параметры этого потока (р и T ) и параметры среды (p0 и T0).

Понятие эксергии потока оказывается весьма удобным для анализа степени термодинамического совершенства того или иного теплового аппарата или установки в целом. В самом деле, рассмотрим какой-либо тепловой аппарат (например, турбину), в который входит поток рабочего тела с параметрами p1 и T1; из аппарата этот поток рабочего тела выходит, имея параметры p2 и T2; внутри аппарата этот поток произвел полезную работу lполезн. Если процесс

внутри аппарата необратим, то, следовательно, в аппарате имеет место потеря эксергии D потока. Эта потеря эксергии в расчете на единицу массы (обозначим ее d), очевидно, равна:

d = (e1– e2) – lполезн.

Если эксергия потока на входе в аппарат равна e1, а на выходе из аппарата е2, то разность величин e1– e2

расходуется на совершение полезной работы lполезн и на потери, обусловленные необратимостью. Если бы процессы в этом аппа-

рате были обратимы, то потеря работоспособности отсутствовала бы (d = 0) и в

этом случае поток совершил бы максимально полезную работу



В самом деле, например, если в адиабатном потоке эксергия между двумя сечениями

потока (индексы 1 и 2) снижается на Δe = e1– е2, то отсюда с учетом (9.30б) получаем: e1– e2= (h1– h2) + T0(s2– s1).

Если этот адиабатный процесс течения обратим, то s1= s2, получаем:



т.е.:



если же процесс идет с увеличением энтропии, то обусловленная необратимостью

потеря работоспособности потока d = T0(s2– s1)

будет, очевидно, равна: d = (e1– e2) – lполезн.

В этом и состоит основная идея эксергетического метода: рабочее тело входит в аппарат с эксергией е1 и, совершив полезную работу lполезн, выходит из аппарата с эксергией е2; при этом потеря работоспособности вследствие

необратимости процессов внутри аппарата определяется по уравнению d = (e1– e2) –lполезн.

Важно подчеркнуть, что этот метод позволяет судить о степени необратимости процессов внутри аппарата по внешней характеристике —разности

эксергий на входе в аппарат и на выходе из него.

28. Эксергетические потери и эксергетический КПД. Закон Гюи-Стодолы.

Эксергия потока теплоты q, отдаваемой

телом с температурой Т, определяется в соответствии с (3.196) следующим

образом: e_q =q(1-T0/T)

где T0— температура окружающей среды.

Если в тепловой аппарат, производящий полезную работу lполезн, входит поток рабочего тела с параметрами p1, T1 и подводится поток теплоты q1

от теплового источника, имеющего температуру Тт, а из аппарата выходит тот же поток рабочего тела с параметрами p2, Т2, то в соответствии со сказанным выше потеря эксергии потоков рабочего тела и теплоты составляет:

d = [(eвх+ eqвх) – eвых] – lполезн.

В том случае, если в тепловом аппарате полезная работа не производится, потеря эксергии, очевидно, составит: d = (eвх+ eqвх) – евых.

В величину d входят потери эксергии, обусловленные как трением, так и теплообменом при конечной разности температур; в величине d учтены и потери теплоты аппаратом, обусловленные теплообменом с окружающей средой.

Для количественной оценки степени термодинамического совершенства того

или иного аппарата используется понятие так называемого эксергетического

КПД, определяемого как



Если процессы в аппарате обратимы, то и с учетом (9.32) ηэкс = 1.

На основе сказанного выше нетрудно установить, что для тепловой машины (например, турбины) эксергетический КПД равен внутреннему относительному.

КПД машины, а для установки в целом —эффективному КПД установки.

Закон Гюи-Стодолы.

Напомним, что, как было показано выше, полезная работа, производимая

изолированной системой, состоящей из источника работы и среды, в случае

протекания в ней необратимых процессов определяется уравнением:



а максимальная полезная работа этой системы определяется уравнением

где и — соответственно начальное и конечное значения энтропии среды,

a S и S0 — начальное и конечное значения энтропии источника работы. Очевидно, что для обратимых процессов, протекающих в изолированной системе,



так как энтропия всей изолированной системы (в случае обратимых процессов)

не должна изменяться.

Но так как уравнение (3.191) записано для Lполезн, т.е. для случая, когда в системе протекают необратимые процессы, а уравнение записано для Ev,

т.е. для случая, когда в системе протекают только обратимые процессы, то



И



Где



увеличение энтропии системы в резуль-

тате протекающих в ней необратимых процессов.

Подчеркнем еще раз, что эксергия Ev — это максимально возможная полезная работа, которую может произвести данная изолированная система, если процессы, ведущие к установлению равновесия в этой системе, будут протекать обратимо (работоспособность системы), a Lполезн — это работа, которую производит та же система в случае необратимости протекающих в ней процессов. Разность этих величин представляет собой потерю эксергии (работоспособности) системы вследствие необратимости процессов, протекающих в ней. Из Ev-Lполезн =… видно, что чем больше степень необратимости этих процессов, т.е. больше разность EV– Lполезн, тем больше потеря эксергии (работоспособности) системы.

Уравнение Ev-Lполезн =… имеет универсальное значение, в частности для изолиро-

ванной системы, состоящей из двух источников теплоты и рабочего тела, совер-

шающего цикл.

D = T0ΔSсист (3.205)

Уравнение (3.205) называют уравнением Гюи—Стодолы по имени французского физика М. Гюи, который впервые вывел это уравнение в 1889 г.,

и словацкого теплотехника А. Стодолы, впервые применившего это уравнение для решения технических задач. Уравнение Гюи—Стодолы находит широкое применение при анализе эффективности работы тепловых установок.
27.