ответы на юилеты по математической логике 2 семестр мирэа. 21. Дизъюнкты, резольвента. Резолютивный вывод из множества дизъюнктов
 Скачать 22.99 Kb. Скачать 22.99 Kb.
|
|
21. Дизъюнкты, резольвента. Резолютивный вывод из множества дизъюнктов. . Пусть S – множество дизъюнктов. Резолюционным выводом из S назовём такую конечную последовательность дизъюнктов С1,....Сn , что для каждого Ci i=1,…n Либо Ci ϵ S, либо Ci ϵ R({Cj,Cк}) 1≤j, k≤I Дизъюнкт C считается резолютивно выводимым из мн. дизъюнктов S, если существует резолютивный вывод из S, последний дизъюнкт которого – С=Cn. Очевидно что C ϵ R*(S). Этот факт обозначается так  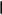 S R С S R СМн дизъюнктов S не подтверждаемо (или невыполнимо) тогда и только тогда, Когда R*(S)= 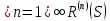 содержит пустой дизъюнкт содержит пустой дизъюнкт То есть если мы при применении метода резолюции к множеству S получим пустой дизъюнкт, то множество S будет неподтверждаемым . 22. Метод резолюций в логике высказываний. Метод резолюции – наиболее эффективный способ алгоритмического доказательства как в логике высказываний так и в логике предикатов именно этот метод построения доказательств составляет основу языка программирования ПРОЛОГ Мы знаем что любую формулу не являющуюся тавтологией можно представить в виде КНФ. Определение. Латерал – это произвольный атом или его отрицание. Дизъюнкция конечного множества литералов называется дизъюнктом Пустой дизъюнкт – это дизъюнкт который не содержит ни одного литерала и является всегда неподтверждённым. Удобнее формулировать сложное высказывание, представленное в виде КНФ как множество дизъюнктов . А каждый дизъюнкт представлять как множество литералов. ТО есть КНФ это конъюнкция конечного множества дизъюнктов , а дизъюнкт – это дизъюнкция конечного множества литералов 23. Предикаты. Кванторы. Операции навешивания кванторов. Основные равносильности содержащие кванторы. Опр. Пусть x1,x2,….xn – символы переменных произвольной природы. Наборы переменных (x1,…,xn) принадлежат множеству S2, которое будем называть предметной областью, а переменные будем называть предметами. N-местным предикатом, определённым на предметной области S2, называют отображение S2 во множестве высказываний. То есть это утверждение о предметных переменных обладающее свойством, что при фиксации значений всех переменных об этом утверждении можно сказать, истинно оно или ложно P(x,y,z) = “ x2 + y2 ≤ z2; x,y,z ϵ R “- трёхместный предикат определённый на R3 Навешивание кванторов: Окр. Пусть P(x) – одноместный предикат. Поставим ему в соответствие высказывание, обозначаемое 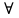 xP(x) (для любого x P(x)), которое истинно тогда и только тогда, когда P(x) тождественно истинный предикат. xP(x) (для любого x P(x)), которое истинно тогда и только тогда, когда P(x) тождественно истинный предикат. О высказывании 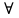 xP(x) говорят, что оно получено из предиката Р навешиванием квантора всеобщности из переменной х xP(x) говорят, что оно получено из предиката Р навешиванием квантора всеобщности из переменной х Опр. Когда Р(х) – одноместный предикат. Поставим ему в соответствие высказывание, обозначаемое 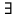 xP(x) (существует х Р(х)), которое ложно тогда и только тогда, когда Р(х) тождественно ложный предикат. О высказывании xP(x) (существует х Р(х)), которое ложно тогда и только тогда, когда Р(х) тождественно ложный предикат. О высказывании 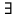 xP(x) говорят, что оно получено из предиката Р навешиванием квантора по переменной х. xP(x) говорят, что оно получено из предиката Р навешиванием квантора по переменной х.Освновные равносильности Закон де Моргана для кванторов (двойственность) ¬( 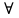 xР(x)) ≡ xР(x)) ≡ 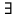 x ¬(Р(x)) x ¬(Р(x))¬( 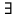 xР(x)) ≡ xР(x)) ≡ 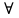 x ¬(Р(x)) x ¬(Р(x))Коммутация одноименных кванторов 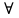 x x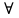 уР(х,у) ≡ уР(х,у) ≡ 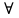 у у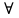 хР(х,у) хР(х,у)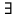 x x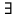 уР(х,у) ≡ уР(х,у) ≡ 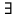 у у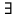 хР(х,у) хР(х,у)Дистрибутивные законы для кванторов 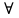 x(Р(x)^Q(x)) ≡ x(Р(x)^Q(x)) ≡ 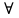 xР(x) ^ xР(x) ^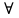 xQ(x) xQ(x)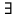 x(Р(x)vQ(x)) ≡ x(Р(x)vQ(x)) ≡ 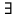 xР(x) v xР(x) v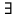 xQ(x) xQ(x)Законы ограничения действ для кванторов 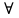 x(Р(x) v Q(у)) ≡ x(Р(x) v Q(у)) ≡ 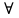 xР(x) v Q(у) xР(x) v Q(у)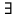 x(Р(x)^Q(у)) ≡ x(Р(x)^Q(у)) ≡ 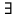 xР(x) ^ xР(x) ^ Q(у) Q(у)* 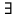 у у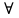 xР(х,у)→ xР(х,у)→ 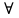 х х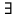 уР(х,у) ≡ И уР(х,у) ≡ И35. Вычисление на машинах Тьюринга. Функции вычислимые по Тьюрингу Определение Конфигурацией машины Т называется всякая запись в явном виде, указывающая состояние считывающей головки и то, что записано на ленте αqi β; α – то слово, что находится слева от головки на листе, β –то, что находится справа. Определение Конфигурация Т, в которой головка смотрит на первую (левую) ячейку массива информации, записанной на ленте, называется правильной конфигурацией. Обычно требуют, чтобы машина Т начинала и заканчивала работу в правильных конфигурациях. Задать машину Тьюринга – значит задать последовательность конфигураций. Переход от одной конфигурации к другой описывается командами Рассмотрим произвольную функцию y=f(x1…xn), где xi – целые неотрицательные числа, y – принимает целое неотрицательное значение. Функция f(x1…xn) называется вычислимой по Тьюрингу, если существует машина Тьюринга, работающая следующим образом: для любой совокупности чисел x1,x2…xn, для которых функция f определена, машина Тьюринга, начав работу из начальной конфигурации q01x1 …1xn, заканчивает работу конфигурацией q01y, где y=f(x1…xn). Если f на совокупности x1..xn не определена, то машина Тьюринга работает бесконечно. |
