Отражение относительно точки. Отражение относительно точки (центральная симметрия)
 Скачать 50.5 Kb.
|
|
Отражение относительно точки (центральная симметрия) Пусть оси обеих отражений пересекаются под прямым углом, т.е.  .Т  еорема. Произведение двух отражений от взаимно перпендикулярных осей есть движение, обладающее следующим свойством: все отрезки, соединяющие две соответственные точки фигур имеют общую середину. Движение, обладающее этим свойством, называют отражением от точки или центральной симметрией (рисунок 56).а 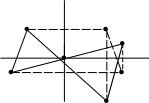 )  б)  A’’ Bo A’ А А' B’’ O Ao  O  A В B’ A’’ Рис.56 Пусть  ,  , точка О – центр отражения, или центр симметрии. Две точки А,А’’, называются симметричными относительно точки О, если точки А, О, А’’ лежат на одной прямой и  , т.е. точка О есть середина отрезка АА''.Пусть и – оси обоих отражений, .   Рассмотрим треугольники: Δ ОААo, Δ ОАoA’, Δ ОА’Bo, Δ ОBА’’. Все они конгруэнтны между собой. Из конгруэнтности этих треугольников вытекает, что:  . Следовательно, точки А, О, А'' лежат на одной прямой и, что  . Следовательно, отрезок АА’’ делится точкой О пополам.Следствие. Отражение от точки, имеет одну двойную точку – центр симметрии и бесконечное множество двойных прямых: этими прямыми будут все прямые, переходящие через центр отражения. |