25 вопрос (Квантили распределений.)
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
25 вопрос (Квантили распределений.) Квантилью ур. Р СВХ наз-ся реш ур-я: Р(Х=хр)=р р – нек. число 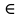 (0;1) (0;1) 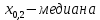  26 вопрос (Основные понятия и задачи математической статистики. Выборка. Выборочное распределение.) Математическая статистика-раздел математики в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Совокупность всех подлежащих изучению объектов относительного некоторого признака(возможных результатов наблюдений производимых в неизменных условиях) называется генеральной совокупностью. Выборочная совокупность(выборкой) называют совокупность объектов отобранных случайным образом из генеральной совокупности. Число объектов генеральной или выборочной совокупности называют её объёмом. Метод статистического исследования заключается в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности. Для получения адекватных оценок характеристики генеральной совокупности необходимо, чтобы выборка была репрезантативной. Условием обеспечения репрезантивности согласно закону больших чисел является соблюдение случайного отбора. Различают выборки с возвратом (повторные ) и безвозвратные(без повторные). В зависимости от конкретного условий применяют слелующие способы отбора 1) простой 2) типический 3) механический 4) серийный 27 вопрос (Выборка и геометрические способы ее представления. Гистограмма, полигон. Эмпирическая функция распределения.) 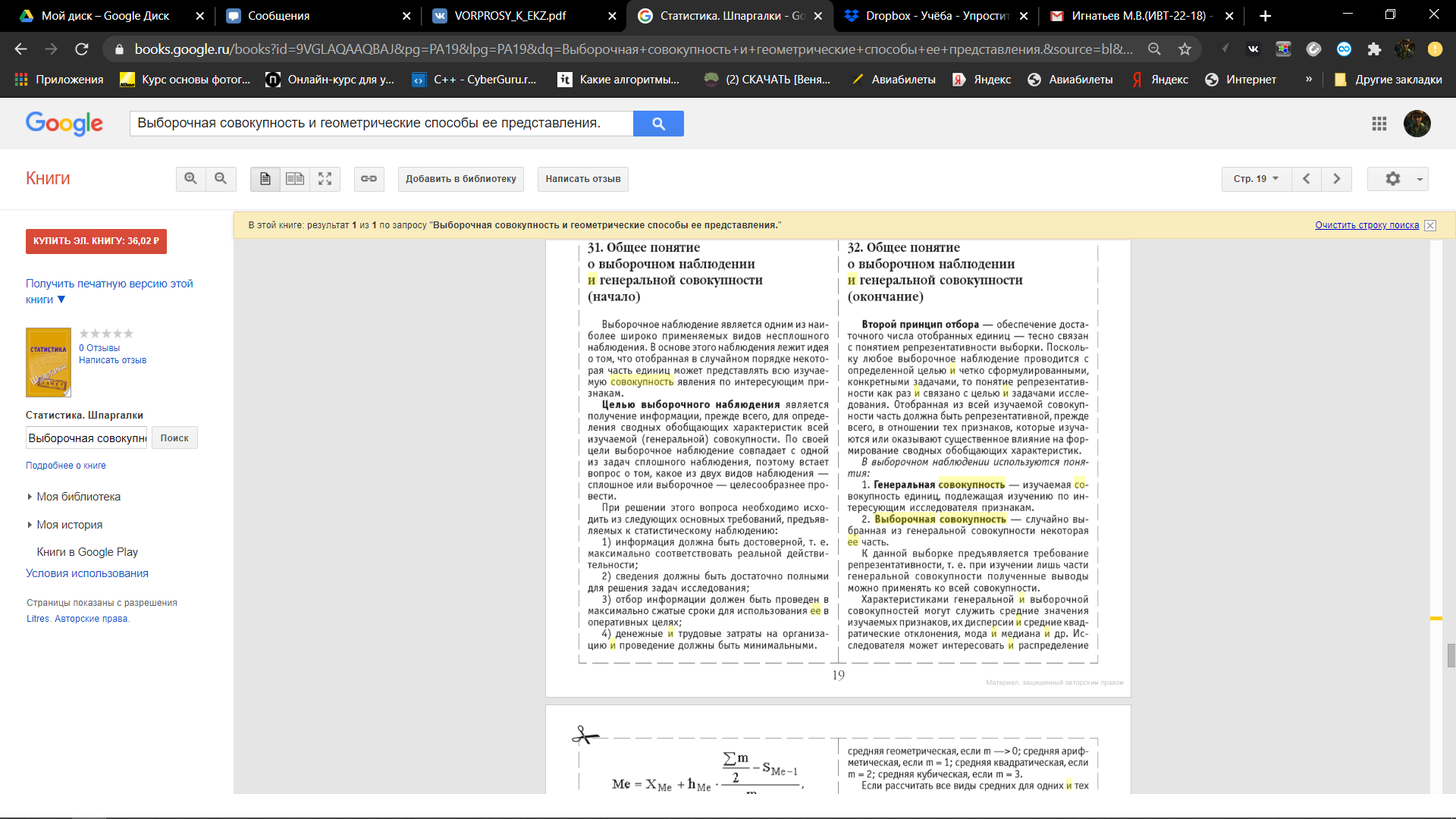 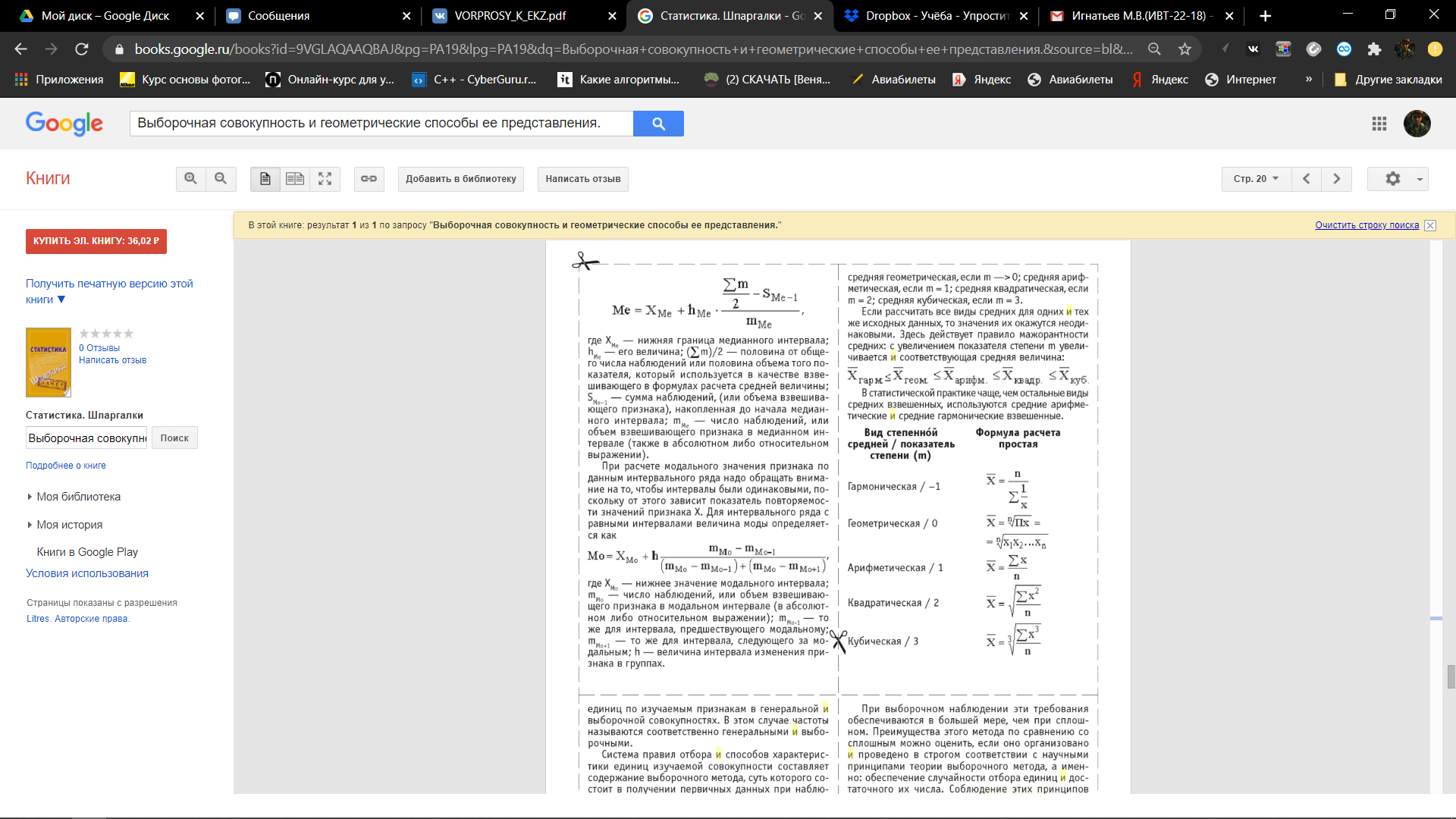 Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле: xi-xi-1 Высоты гистограммы определяется по формуле: 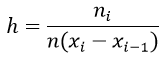 Формула размаха выборки R: R=xmax−xmin Количество интервалов в выборке определяется по формуле: k≈1+log2n≈1+3,221·lgn Длина l интервала гистограммы, формула: l=R/n Формула эмпирической плотности распределения выборки имеет вид: 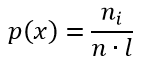 хi— значения частот; ni— частоты; wi— относительные частоты; n — объём выборки; Одним из способов обработки вариационного ряда является построение эмпирической функции распределения. Эмпирической (статистической) функцией распределения называется функция
Для нахождения значений эмпирической функции удобно Очевидно, что При увеличении числа n наблюдений (опытов) относительная частота события |
