ОТН 3.5 ТЖ(1)(1). 3. 5 Топологический метод расчета надежности резервированных систем

• Название: 3. 5 Топологический метод расчета надежности резервированных систем
• Дата: 14.12.2022
• Размер: 72.02 Kb.
• Имя файла: ОТН 3.5 ТЖ(1)(1).docx
• Тип: Документы; #844786

3.5 Топологический метод расчета надежности резервированных систем

Условия задачи и исходные данные

На рис.3.5.1 приведена структурная схема некоторой системы с восстановлением. Значения интенсивности отказа и времени восстановления каждого элемента, вид и кратность резервирова-

ния, а также число ремонтных бригад заданы в табл. 3.5.1

Используя данные таблицы, построить систему с резервированием. Найти выигрыш надежности по времени наработки на отказ:

GT =ТР / Т0

где ТР – время наработки на отказ для резервированной системы, Т0 – время наработки на отказ для нерезервированной системы.



Рис.3.5.1 Структурная схема системы для выполнения практической работы

№ варианта	Интенсивность отказа, 1/ч			Время восста- новления, ч			Количество рем. бригад	Вид резервиро- вания	Реализация резервирования, кратность резервирования m
	1	2	3	ТВ1	ТВ2	ТВ3			Элемент 1	Элемент 2	Элемент 3
3	2·10-4	2·10-4	2·10-4	10	10	10	1	Скользящее	m = 3

Табл. 3.5.1 Исходные данные
Расчет

1. Построим структурную схему системы после резервирования

Структурная схема системы после резервирования представлена на рисунке 3.5.2.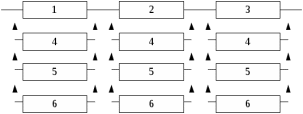

Рис. 3.5.2 Структурная схема системы после резервирования

2. 
   Найдем время наработки на отказ системы без резервирования. Для экспоненциального закона распределения интенсивностей отказов и восстановлений получим:
   

Время наработки на отказ системы без резервирования:

c = 1 + 2 + 3 = 6·10^-4 час^-1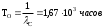

2. 
   Найдем интенсивность отказа первого элемента после резервирования 1р, для этого воспользуемся формулами (6)–(8) и вышеприведенной табл. 3.5.2.
   

Табл. 3.5.2.Интенсивности переходов i в зависимости от вида резервирования

Вид резервирования	i
Скользящее ((n – т) основных, т резервных элементов)	(n–m)i, i = 1, 2, …,m+1

На основании данных из таблицы для постоянно включенного резерва получим:

1 = (n-m)1 = 31

2 = (n-m)2 = 31

3 = (n-m)3 = 31

4 = (n-m)4 = 31

где 1, 2, 3 , 4– интенсивности переходов для графа(см.рис.3.5.3)



Рис.3.5.3 Граф состояний резервированной системы с идентичными элементами

Из формулы (8) с учетом того, что обслуживанием занимается одна ремонтная бригада (r = 1), получим:

M1 = ₁;

M2 = ₁;

M3 = ₁;

M4 = ₁;

Используя формулу (6), находим наработку на отказ дублированного элемента 1: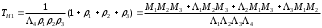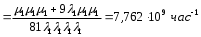



Учитывая экспоненциальный закон распределения интенсивностей переходов, найдем интенсивность отказа дублированного элемента 1: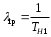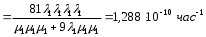



Интенсивность восстановления резервированного элемента 1:

_1p = M4= ₁ = 1/Т_В1 = 0,1 час^-1

4. Аналогично найдем интенсивность отказа и интенсивность восстановления для резервированного (дублированного) элемента 2 и 3: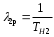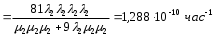



_2p = M4= ₂ = 1/Т_В2 = 0,1 час^-1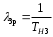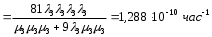



_3p = M4= ₃ = 1/Т_В3 = 0,1 час^-1

2. 
   Найдем время наработки на отказ системы с резервированием. По экспоненциальному закону распределения интенсивностей отказов получим: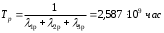
   

2. 
   Выигрыш надежности по времени наработки на отказ:
   

GT =ТР / Т0= 2,587·10 ⁹ / 1,67·10 ³ =1,549·10 ⁶.