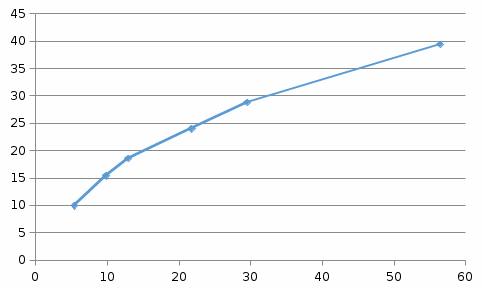
Показать, что адсорбция аргона на кокосовом угле подчиняется уравнению Фрейндлиха и найти графически константы этого уравнения. 3. Показать, что адсорбция аргона на кокосовом угле подчиняется уравнению Фрейндлиха и найти графически константы этого уравнения по следующим данным Давление, см рт ст.
 Скачать 36.7 Kb. Скачать 36.7 Kb.
|
|
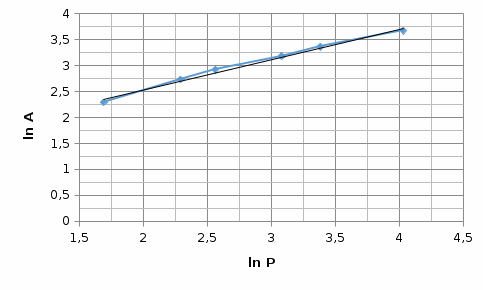
3. Показать, что адсорбция аргона на кокосовом угле подчиняется уравнению Фрейндлиха и найти графически константы этого уравнения по следующим данным: Давление, см. рт. ст. 5,42 9,84 12,9 21,8 29,5 56,4 Адсорбированное количество, см3/г 9,9 15,4 18,6 24,0 28,8 39,4 Решение: На практике часто для аналитического описания зависимости адсорбции на твердом адсорбенте от концентрации адсорбтива применяется эмпирическое уравнение Фрейндлиха: где β, n – эмпирические коэффициенты, зависящие от природы адсорбтива и температуры. Уравнение Фрейндлиха представляет собой уравнение параболы, поэтому оно описывает не всю изотерму адсорбции, а только ее криволинейный участок.  Рис.1. Графическое определение констант уравнения Фрейндлиха Постоянные уравнения Фрейндлиха определяются на основе опытных данных. Для этого уравнение Фрейндлиха приводят к линейному виду (логарифмируют): и строят график в координатах lnA = f(lnр), который представляет собой прямую (рис. 1). Тангенс угла наклона равен n, а отрезок, отсекаемый прямой на оси ординат, – lnβ. Построим изотерму адсорбции, которая подчиняется уравнению Фрейндлиха:
Построим график зависимости ln (X) = f(lnP):
Вычислим коэффициенты в уравнении Фрейндлиха. Согласно графика зависимости, тангенс угла наклона прямой равен n, а тангенс угла наклона равен отношению противолежащего катета к прилежащему, то есть: tgα = n; tg α = 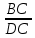 = = 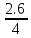 = n; = n;n = 0.65 Отрезок, отсекаемый прямой на оси ординат равен lnβ: lnβ= 1.1. Тогда коэффициент β: β = 0.333. |