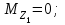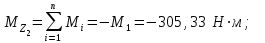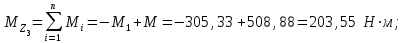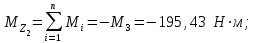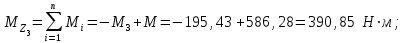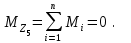Задание 3 – Проектировочный расчет вала фрикционной передачи из условий прочности и жесткости при кручении. Пример. 3 Задание 3 Проектировочный расчет вала фрикционной передачи из условий прочности и жесткости при кручении
 Скачать 287.45 Kb. Скачать 287.45 Kb.
|
|
3 Задание 3 – Проектировочный расчет вала фрикционной передачи из условий прочности и жесткости при кручении От электродвигателя на вал I посредством ременной передачи передается На вал I посредством ременной передачиот электродвигателя (Э) передается мощность Р при частоте вращения n. С вала I посредством фрикционной передачи поступает на вал II мощность Р1. С валов I и II поступают к рабочим машинам мощности Р2, Р3, Р4и Р5. Сечения валов считать по всей длине постоянными. Принять допускаемое касательное напряжение [τ]=80 МПа, модуль сдвига G=8·104 МПа. Значение допускаемой относительной деформации [ϴ] приведено в исходных данных. Требуется: 1 Определить основные характеристики передач. 2 Определить крутящий момент на каждом участке нагружения вала и построить эпюры. 3 Определить диаметры валов из условий прочности и жесткости Полученное по расчету значение диаметра (мм) округлить до ближайшего числа, оканчивающегося на 0 или 5.
Решение: 1 Рассмотрим заданную схему. На вал I насажены три шкива; на вал II насажены четыре шкива.Обозначим буквами А, В, С, D и E границы участков вала I и буквами А, В, С, D, E и F границы участков вала II. Границами участков являются сечения посадки шкивов и крепления валов (подшипники). От электродвигателя на вал посредством ременной передачи (шкив диаметром D =200 мм и шкив диаметром D1=350 мм) передается мощность Р=25 кВт при частоте вращения вала электродвигателя n=800 об/мин. С вала I посредством фрикционной передачи (шкив диаметром D2=250 мм и шкив диаметром D3 =480 мм) поступает на вал II мощность Р1=15 кВт. С вала I снимается мощность Р2= 10 кВт, а с вала II – мощности Р3=5 кВт, Р4=7 кВт и Р5=3 кВт. 2 Определим усилия на вале I . Вал I получает от электродвигателя мощность Р=25 кВт посредством ременной передачи. Тогда на шкиве в сечении С будет мощность равная Р=25 кВт. Полученная мощность распределяется по шкивам, причем 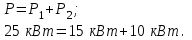 2.1 Определим частоту вращения вала I. Используем соотношение 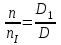 . . Откуда находим частоту вращения nIвала I: 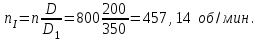 2.2 Определим угловую скорость вращения вала I:  2.3 Определим внешние крутящие моменты: - крутящий момент М на шкиве в сечении С: 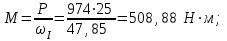 - крутящий момент М1 на шкиве в сечении В: 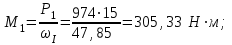 - крутящий момент М2 на шкиве в сечении D: 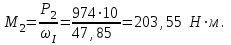 3 Построим эпюру крутящих моментов Mz для вала I. В сечениях А и Е подшипники заменим шарнирными опорами. Нанесем на схему внешние крутящие моменты: М, М1 и М2. Вал состоит из четырех участков нагружения: участок АВ, участок ВС, участок СD и участок DЕ. Для определения крутящих моментов Мz используем метод сечений: на каждом участке проведем сечение, перпендикулярное оси вала; отбросим одну часть; рассмотрим равновесие оставшейся части. Рассмотрим каждый участок в отдельности. Составим уравнения крутящих моментов Мzна каждом участке вала. По условному правилу знаков, если внешний крутящий момент направлен против хода часовой стрелки, если смотреть со стороны поперечного сечения, то подставляем его значение в формулу со знаком «+». Условно примем внешний крутящий момент М в сечении С за положительный (направлен против хода часовой стрелки); тогда по условию равновесия крутящие моменты М1 в сечении В и М2в сечении D - отрицательные (направлены по часовой стрелки). Крутящий момент возникает только на участках между шкивами. Участок АВ:  Участок ВС: 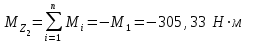 Участок CD: 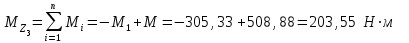 Участок DE: 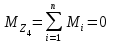 По найденным значениям крутящих моментов для каждого участка строим эпюру крутящих моментов Mz. 4 Определим усилия на вале II . Вал II получает от вала I мощность Р1=15 кВт посредством фрикционной передачи. Тогда на шкиве в сечении С будет мощность равная Р1=15 кВт. Полученная мощность распределяется по шкивам, причем  4.1 Определим частоту вращения вала II. Используем соотношение 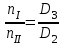 . . Откуда находим частоту вращения nIIвала II:  4.2 Определим угловую скорость вращения вала II:  4.3 Определим внешние крутящие моменты: - крутящий момент М3 на шкиве в сечении В:  - крутящий момент М1 на шкиве в сечении С: 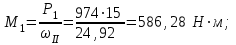 - крутящий момент М4 на шкиве в сечении D: 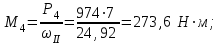 - крутящий момент М5 на шкиве в сечении E:  5 Построим эпюру крутящих моментов Mz для вала II. Подшипники в сечениях А и F заменим шарнирными опорами. Нанесем на схему внешние крутящие моменты: М1, М3, М4 и М5. Вал состоит из пяти участков нагружения: участок АВ, участок ВС, участок СD, участок DЕ и участок ЕF. Для определения крутящих моментов Мz используем метод сечений: на каждом участке проведем сечение, перпендикулярное оси бруса; отбросим одну часть бруса; рассмотрим равновесие оставшейся части. Рассмотрим каждый участок в отдельности. Составим уравнения крутящих моментов Мzна каждом участке вала. По условному правилу знаков, если внешний крутящий момент направлен против хода часовой стрелки, если смотреть со стороны поперечного сечения, то подставляем его значение в формулу со знаком «+». Условно примем внешний крутящий момент М1 на шкиве в сечении С за положительный (направлен против хода часовой стрелки); тогда по условию равновесия крутящие моменты М3, М4и М5 - отрицательные (направлены по ходу часовой стрелки). Крутящий момент возникает только на участках между шкивами. Участок АВ:  Участок ВС: 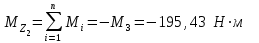 Участок CD:  Участок DE:  Участок EF:  По найденным значениям крутящих моментов для каждого участка строим эпюру крутящих моментов Mz. 6 Определим из условия прочности диаметр dIвала I. Условие прочности при кручении: 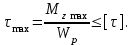 Полярный момент сопротивления для сплошного круглого сечения определяется по формуле:  Максимальный крутящий момент по абсолютному значению на вале I равен:  Требуемый диаметр вала I из условия прочности будет определяться по формуле:  Округляя величину диаметра, получаем: dI=30 мм. 7 Определим из условия жесткости диаметр dIвала I. Условие жесткости при кручении: 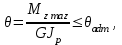 Полярный момент инерции для сплошного круглого сечения определяется по формуле: 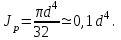 Максимальный крутящий момент по абсолютному значению на вале I равен: Требуемый диаметр вала I из условия жесткости будет определяться по формуле:  Округляя величину диаметра, получаем: dI=45 мм. Из двух полученных значений выбираем наибольшее значение диаметра вала. Окончательно назначаем диаметр вала: dI=45 мм. 8 Определим из условия прочности диаметр dIIвала II. Условия прочности при кручении: 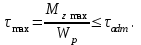 Полярный момент сопротивления для сплошного круглого сечения определяется по формуле:  Максимальный крутящий момент по абсолютному значению на вале II равен:  Требуемый диаметр вала II из условия прочности будет определяться по формуле:  Округляя величину диаметра, получаем: dII=30 мм. 9 Определим из условия жесткости диаметр dIIвала II. Условие жесткости при кручении: 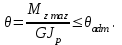 Полярный момент инерции для сплошного круглого сечения определяется по формуле: 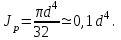 Максимальный крутящий момент по абсолютному значению на вале II равен:  Требуемый диаметр вала II из условия жесткости будет определяться по формуле:  Округляя величину диаметра, получаем: dII=50 мм. Из двух полученных значений выбираем наибольшее значение диаметра вала. Окончательно назначаем диаметр вала II: dII=50 мм. 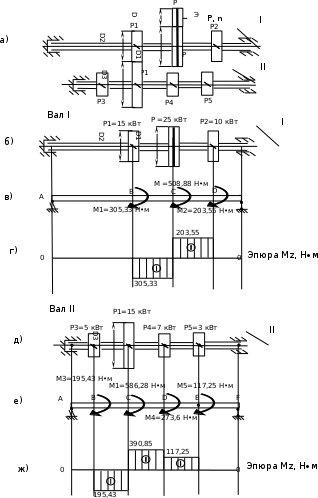 Рисунок 2 – Схемы валов, эпюры крутящих моментов Таблица 1 – Результаты расчета
Продолжение таблицы 3.3
| ||||||||||||||||||||||||||||||||||||||