Сопромат РПР V. Отчет по расчетнопроектировочной работе 5 по дисциплине
 Скачать 37.4 Kb. Скачать 37.4 Kb.
|
 Министерство образования и науки Российской Федерации Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Институт/Факультет Архитектуры и строительства Кафедра Сопротивления материалов и строительной механики РАСЧЕТ СТУПЕНЧАТОГО ВАЛА НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ Отчет по расчетно-проектировочной работе №5 по дисциплине сопротивление материалов Выполнил студент группы СМ-14-2 П.А.Чернышев Принял доцент к.т.н В.П.Ященко Иркутск 2015 Цель работы:
Дано: Ступенчатый вал круглого поперечного сечения; L = 0.4 м; M1 = 1.7 кН*м; M2 = 2.4 кН*м; M3 = 2.7 кН*м; материал – сталь: G = 0.8*105 МПа; [τ] = 80 МПа; [θ°] = 0.4 град/м (см. приложение А). 1 Построение эпюры крутящих моментов Tz Для начала необходимо будет сделать разрезы в каждой из составных частей вала. Затем, отбросив одну из частей, заменить ее действие системой крутящих моментов. В данной задаче под рассмотрение попадает крутящий момент Tz. Итак, рассмотрим каждый из участков – всего их будет 3 (см. приложение А): I участок: 0 ≤ Z1 ≤ L ΣMZ = 0: Tz(Z1) – M2 = 0 Отсюда Tz(Z1) = M2 = 2.4 кН*м = const II участок: 0 ≤ Z2 ≤ 2*L ΣMZ = 0: Tz(Z2) – M2 + M3 = 0 Отсюда Tz(Z2) = M2 - M3 = 2.4 – 2.7 = -0.3 кН*м = const III участок: Z3 = 3*L (нет смысла проводить сечение между заделкой и последним участком, можно провести его как раз на границе участков L и 3L, так как в ступени вала диаметром d2 будет действовать только один крутящий момент Tz(Z3) = const) ΣMZ = 0: Tz(Z3) – M2 +M3 – M1= 0 Отсюда Tz(Z3) = M2 –M3 + M1= 2.4 – 2.7 + 1.7 = 1.4 кН*м = const 2 Из условий прочности и жёсткости определить диаметры круглого поперечного сечения ступеней вала (d1 и d2) Из эпюры «Tz» видно, что в первой ступени вала – диаметром d1: Tmax1 = 2.4 кН*м. Из эпюры «Tz» также видно, что во второй ступени вала – диаметром d2: Tmax2+ = 1.4 кН*м. Теперь определим непосредственно диаметры поперечных сечений d1 и d2: 1 ступень: Из условия прочности: τmax ≥ Tmax/Wρ≤ [τ] Wρ = π*d3/16 – для круглого поперечного сечения Отсюда d11 ≥ 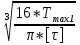 = = 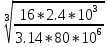 = 0.053 м = 53 мм = 0.053 м = 53 ммИз условия жёсткости: θ° = 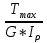 * * 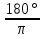 ≤ [θ°] ≤ [θ°]Iρ = π*d4/32 – для круглого поперечного сечения Отсюда d12 ≥ 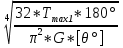 = = 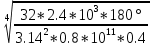 = 0.081 м= 81 мм = 0.081 м= 81 ммИз этих вычислений видно, что больший диаметр – это диаметр d12. Следовательно, берем d1 = d12 = 81 мм. 2 ступень: Из условия прочности: τmax ≥ Tmax/Wρ≤ [τ] Wρ = π*d3/16 – для круглого поперечного сечения Отсюда d21 ≥ 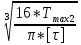 = = 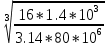 = 0.045 м = 45 мм = 0.045 м = 45 ммИз условия жёсткости: θ° = 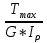 * * 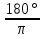 ≤ [θ°] ≤ [θ°]Iρ = π*d4/32 – для круглого поперечного сечения Отсюда d22 ≥ 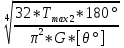 = = 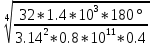 = 0.071 м= 71 мм = 0.071 м= 71 ммИз этих вычислений видно, что больший диаметр – это диаметр d22. Следовательно, берем d2 = d22 = 71 мм. 3 Построение эпюры абсолютных углов закручивания φ Для того, чтобы построить эпюру абсолютных углов закручивания, необходимо рассчитать по закону Гука деформации при кручении в сечениях a, b, c, d и e данного вала и по этим значениям построить график. Этот график должен соответствовать эпюре Tz. Для начала нужно провести эти самые поперечные сечения. В данном случае их будет пять (см. приложение А). Найдем все эти деформации, как и было сказано выше, по закону Гука: φ = 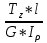 Сразу определим значения моментов инерции Iρ1 и Iρ2: Iρ1 = π*d14/32 = 3.14*0.0814/32 = 4.226*10-6 м4 Iρ2 = π*d24/32 = 3.14*0.0714/32 = 2.495*10-6 м4 φa = 0 – заделка (сечение закреплено) φb = φab = 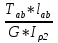 = = 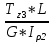 = = 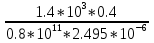 = 2.8*10-3 рад = 2.8*10-3 радφc = φb + φbc = φb + 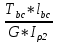 = φb + = φb + 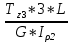 = 2.8*10-3 + = 2.8*10-3 + 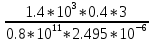 = 11.2*10-3 рад = 11.2*10-3 радφd = φc + φcd = φc + 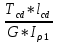 = φc + = φc + 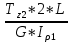 = 11.2*10-3 + = 11.2*10-3 + 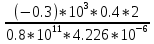 = 10.5*10-3 рад = 10.5*10-3 радφe = φd + φde = φd + 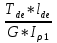 = φd + = φd + 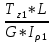 = 10.5*10-3 + = 10.5*10-3 + 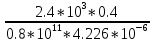 = 13.34*10-3 рад = 13.34*10-3 радПриложение А |
