310. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружают в масло.

• Название: 310. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружают в масло.
• Дата: 23.12.2022
• Размер: 252 Kb.
• Имя файла: 5189.doc
• Тип: Документы; #860739

310. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружают в масло. Какова плотность масла , если угол расхождения нитей при погружении в масло остаётся неизменным? Плотность материала шариков ₀ = 1,5·10³ кг/м³, диэлектрическая проницаемость масла  = 2,2.

Дано:
кг/м

Решение.
в воздухе в масле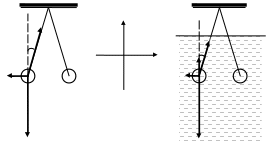


















Шарики в воздухе.

Запишем для одного из шариков условие равновесия по второму закону Ньютона в векторной форме и в проекциях на оси и :

;

;

,

где – сила кулоновского отталкивания в воздухе;

– сила тяжести;

– сила натяжения нити в воздухе;

– угол, на который разошлись шарики.

Поделим первое уравнение на второе:

;

.
Шарики в масле.

Условие равновесия:

;

;

,

где – сила кулоновского отталкивания в масле;

– сила натяжения нити в масле;

– архимедова сила.

Поделим первое уравнение на второе:

;

.

Приравняем два выражения для :

.

Силы кулоновского отталкивания между шариками в воздухе и в масле:

;

,

где Ф/м – электрическая постоянная;

– диэлектрическая проницаемость масла;

– заряд каждого шарика;

– расстояние между шариками.

Силу тяжести представим в виде:

,

где – плотность материала шарика;

– объём шарика.

Сила Архимеда, выталкивающая шарик из масла, равна:

,

где – плотность масла.

Тогда получаем:

;

;

.

Отсюда найдём плотность масла:

;

;

кг/м³.
Ответ: кг/м³.

311. Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов ₁ = + 5·10^-8 и ₂ = – 9·10^-8 Кл/м² заполнено стеклом ( = 7). Определить напряжённость поля между плоскостями и вне плоскостей.

Дано:
Кл/м2
Кл/м2

Решение.

Напряжённость поля равномерно заряженной бесконечной плоскости:

,

где – поверхностная плотность заряда;

Ф/м – электрическая постоянная;

– диэлектрическая проницаемость среды.

Вектор напряжённости направлен от положительно заряженной плоскости или к отрицательно заряженной.

Согласно принципу суперпозиции, для двух плоскостей результирующий вектор напряжённости равен:

.

Сделаем рисунок.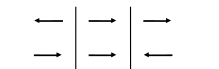







Между плоскостями векторы и сонаправлены, поэтому напряжённость суммарного поля направлена также (от плоскости 1 к плоскости 2) и равна по величине:

;

В/м.
Вне плоскостей векторы и противоположно направлены, поэтому вектор напряжённости суммарного поля направлен так же, как больший по величине вектор, то есть, как вектор (к пластине 2), а величина напряжённости (диэлектрическую проницаемость среды считаем равной 1):

;

В/м.
Ответ:

между плоскостями: В/м;

вне плоскостей: В/м.

322. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряжённость и потенциал поля в точке, находящейся на расстоянии 5 см от зарядов.

Дано:
нКл	Кл
см	м
см	м

Решение.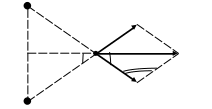













Напряжённость и потенциал поля точечного заряда равны:

,

,

где Ф/м – электрическая постоянная;

– расстояние от точки, в которой рассматривается поле, до заряда.

Поскольку точка отстоит на равном расстоянии от обоих зарядов, а сами заряды одинаковы, то напряжённость и потенциал поля каждого заряда по отдельности в точке будут равны соответственно:

;

.

По принципу суперпозиции электрических полей, для результирующего поля:

, .

Из треугольника определим угол :

.

Рассчитаем напряжённость результирующего поля в точке , используя теорему косинусов:



В/м.

Рассчитаем потенциал результирующего поля в точке :

;

В.

Ответ: В/м, В.

333. Электрон с энергией 400 эВ из бесконечности движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радикалом R = 10 см. Определить минимальное расстояние a, на которое приблизится электрон к поверхности сферы, если заряд её q = – 10 нКл.

Дано:
эВ	Дж
см	м
нКл	Кл
Кл

Решение.

Потенциал поля равномерно заряженной сферы вне поверхности равен:

,

где – заряд сферы;

– радиус сферы;

– расстояние до поверхности сферы.

При перемещении электрического заряда из точки 1 с потенциалом в точку 2 с потенциалом , силы электрического поля совершают работу:

.

Заряд электрона равен (здесь – элементарный заряд). Электрон и сфера заряжены одноимённо, то есть, отталкиваются друг от друга. Следовательно, чтобы электрон приблизился к сфере из точки 1 в точку 2, он должен совершить работу против сил поля:

.

По условию задачи:

, .

Тогда работа равна:

.

Эту работу электрон может совершить только за счёт убыли своей кинетической энергии. Тогда минимальное расстояние , на которое электрон приблизится к поверхности сферы, найдём из условия:

;

;

;

м см.

Ответ: см.

344. Вычислить ёмкость батареи, состоящей из трёх конденсаторов ёмкостью 1 мкФ каждый, при всех возможных случаях их соединения.

Дано:
мкФ

Решение.

Ёмкость батареи:

– при последовательном соединении конденсаторов;

– при параллельном соединении конденсаторов.

При соединении трёх конденсаторов возможны четыре различных случая.
1) Три конденсатора соединены параллельно.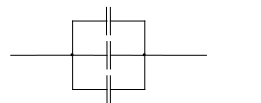











Ёмкость батареи:

;

мкФ.
2) Два конденсатора соединены последовательно, а третий – с ними параллельно.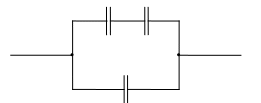



Ёмкость батареи:

;

мкФ.
3) Два конденсатора соединены параллельно, а третий – с ними последовательно.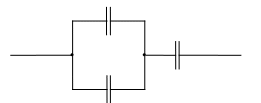







Ёмкость батареи:

;

мкФ.
4) Три конденсатора соединены последовательно.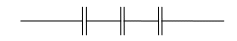







Ёмкость батареи:

;

мкФ.
Ответ: 1) мкФ; 2) мкФ; 3) мкФ; 4) мкФ.

355. Три сопротивления r₁ = 12 Ом, r₂ = 4 Ом, r₃ = 10 Ом соединены параллельно. Общий ток в цепи 0,3 А. Найти силу тока, идущего через сопротивление r₂.

Дано:
Ом
Ом
Ом
А

Решение.

Общее сопротивление цепи, состоящей из трёх параллельно соединённых резисторов:

.

Следовательно, падение напряжение на всей цепи (закон Ома):

,

где – общая сила тока в цепи.

Поскольку при параллельном соединении на каждом резисторе падает напряжение , то по закону Ома, через сопротивление течёт ток силой:

;

А.

Ответ: А.

366. Внутреннее сопротивление батареи аккумуляторов r₁ = 3 Ом. Сколько процентов от точного значения ЭДС составляет ошибка, если, измеряя разность потенциалов на зажимах батареи вольтметром с сопротивлением R = 200 Ом, принять её равной ЭДС?

Дано:
Ом
Ом

Решение.

Составим схему цепи.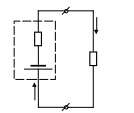



батарея







Согласно закону Ома для полной цепи, сила тока в цепи равна:

,

где – ЭДС батареи;

– внутреннее сопротивление батареи;

– сопротивление нагрузки (в данном случае – вольтметра).

Показания вольтметра, равные напряжению на зажимах батареи (в данном случае будут равны напряжению на вольтметре):

.

Если принять показания вольтметра равными ЭДС батареи, то будет совершена относительная ошибка:



.

Ответ: .

377. Две электрические лампочки с сопротивлениями R₁ = 360 Ом и R₂ = 240 Ом включены в цепь параллельно. Какая из лампочек потребляет большую мощность и во сколько раз?

Дано:
Ом
Ом

Решение.

Если на лампочке сопротивлением падает напряжение , то лампочка потребляет мощность:

.

Следовательно, при параллельном подключении лампочек, когда на них падает одно и то же напряжение, большую мощность будет потреблять лампочка с меньшим сопротивлением, то есть, в данном случае, лампочка 2.

Определим, во сколько раз мощность, потребляемая лампочкой 2, больше, чем мощность, потребляемая лампочкой 1:

;

.

Ответ: мощность, потребляемая лампочкой 2, в 1,5 раза больше.