19 варинат. 3исследование напряженнодеформированного состояния рвс 26
 Скачать 3.79 Mb. Скачать 3.79 Mb.
|
|
СОДЕРЖАНИЕ СОДЕРЖАНИЕ 4 ВВЕДЕНИЕ 5 1ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ 7 1.1 Анализ напряженно-деформированного состояния твердых тел методом конечных элементов 7 1.2 Выбор упругопластической модели деформирования металлов 9 2АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ ТРУБОПРОВОДА 13 2.1 Определение кольцевых и продольных напряжений горизонтальной трубы круглого сечения 13 2.2 Моделирование П-образного компенсатора 19 2.3 Моделирование Z-образного компенсатора 23 3ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ РВС 26 3.1 Построение геометрической модели резервуара 26 3.2 Моделирование напряженно-деформированного состояния 28 3.3 Моделирование вертикального резервуара на грунтовой подушке и построение диаграммы радиальных перемещений 33 3.4 Моделирование сферической крыши резервуара 37 3.5 Моделирование резервуара с Z-образным компенсатором 40 ВВЕДЕНИЕ К группе универсальных CAE-систем относятся программные средства численного анализа, охватывающие широкий круг задач, связанных с изучением различных физических процессов в прикладных и научныхзадачах. Наиболеераспространены системы, использующие решение систем дифференциальных уравнений в частных производных методом конечных элементов(МКЭ), хотя используются и системы, основанные на методах конечных разностей и конечных объемов.Существующие CAE-системы можно подразделить на инженерные и научные. Первые, как правило, ориентированы на решение определенного класса задач (например, механики – CosmosWorks, электричество и магнетизм – CosmosEMS и др.). Научные исследовательские пакеты, например, ANSYS, COMSOLMultiphysics, FlexPDE, обладают большей гибкостью и позволяют решать задачи в самых различных областях. Диапазон применения таких пакетов очень широк. Наряду с решением научных физических задач они находят применение в машиностроении, электронике, авиа- и ракетостроении, химии, биологии и других прикладных научно-технических направлениях. В данной работе будет рассматриваться только прямая задача, которая и является основной при проектировании различных стальных конструкций. Таким образом мы можем воссоздать реальную ситуацию при помощи математических вычислений и даже полностью визуализировать ее для того, чтобы определить, какими предельными параметрами ограничены условия, в которых может функционировать данная конструкция. ANSYS - это профессиональный конечно-элементный расчетный комплекс, позволяющий решать задачи прочности, теплообмена, электромагнетизма, гидрогазодинамики как по отдельности, так и совместно, в связанной постановке. В настоящей работе будут решены несколько задач теории прочности, а также рассмотрены некоторые вопросы устойчивости строительных конструкций. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ 1.1 Анализ напряженно-деформированного состояния твердых тел методом конечных элементов В основе метода конечных элементов лежит представление континуального твердого тела с бесконечным числом степеней свободы в виде ряда конечных элементов, соединенных между собой в узловых точках. Силовые взаимодействия между конечными элементами передаются через узлы, перемещения которых являются неизвестными. Число степеней свободы одного элемента определяется числом узловых перемещений. Перемещения внутри элемента описываются функцией координат 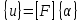 , (1.1) , (1.1)где 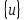 – вектор узловых перемещений; – вектор узловых перемещений;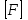 – координатная матрица; – координатная матрица;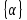 – вектор неизвестных коэффициентов. – вектор неизвестных коэффициентов.В дальнейшем все соотношения метода конечных элементов выражаются через узловые перемещения, которые и являются неизвестными, 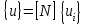 , (1.2) , (1.2)где 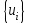 – вектор узловых перемещений; – вектор узловых перемещений;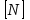 – матрица функций формы. – матрица функций формы.Деформации внутри конечного элемента определяются соотношениями Коши 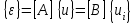 , (1.3) , (1.3)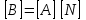 , (1.4) , (1.4) где 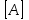 – матрица операций дифференцирования. – матрица операций дифференцирования.Напряжения связаны с деформациями законом Гука: 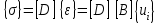 , (1.5) , (1.5)где 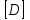 – матрица упругости, определяемая свойствами материала. – матрица упругости, определяемая свойствами материала.Для узлов сетки конечных элементов вводят вектор узловых сил 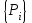 и вектор узловых перемещений и вектор узловых перемещений 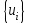 : :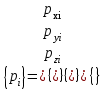  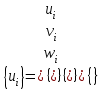 . (1.6) . (1.6)Поставленная задача относится к разделу теории упругости и в данном случае наиболее эффективным оказался вариационный метод её решения. В частности, согласно принципу Лагранжа, можно записать условие минимума полной потенциальной энергии тела в вариационной постановке 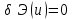 , (1.7) , (1.7)где 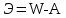 – полная энергия, равная разности потенциальной энергии деформации и работы внешних сил соответственно. – полная энергия, равная разности потенциальной энергии деформации и работы внешних сил соответственно.Тогда, для возможных перемещений получается 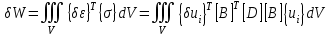 , (1.8) , (1.8)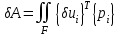 . (1.9) . (1.9)После подстановки этих выражений в (1.7) получается основная формула метода конечных элементов 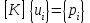 , (1.10) , (1.10)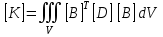 . (1.11) . (1.11)где 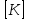 – матрица жесткости конечного элемента. – матрица жесткости конечного элемента.1.2 Выбор упругопластической модели деформирования металлов Необходимость моделирования пластических свойств металлов возникает, когда подвергнутые нагрузке детали и отдельные элементы конструкций работают за пределами упругости. Как показано на рисунке 1.1, металлы в начале нагружения имеют упругую область, в которой деформации пропорциональны нагрузке, но выше предела упругости 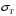 возникают необратимые пластические деформации. возникают необратимые пластические деформации.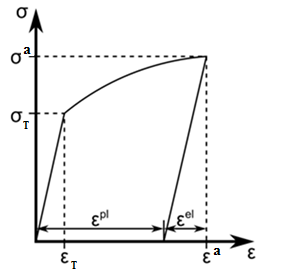 Рисунок 1.1 Диаграмма деформаций для металлов Моделирование материалов с упругопластическим поведением начинается с разложения полной деформации на упругую и пластическую части и создания отдельных моделей для каждой из них. Основными характеристиками перехода к пластической модели является: – критерий текучести, который определяет состояние металла при переходе от его упругого поведения к упругопластическому поведению; – закон текучести, который определяет приращение пластической деформации от приращения нагрузки; – закон упрочнения, который определяет эволюцию критерия текучести при пластической деформации. Для общей модели пластичности, которая включает в себя произвольный путь нагружения, в теории текучести добавочный тензор деформаций разлагается на приращения упругих и пластических деформаций 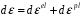 . (1.12) . (1.12)Затем определяются приращения упругих напряжений, которые пропорциональны приросту упругой деформации 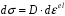 , (1.13) , (1.13)а выбранная пластическая модель дает приращение пластических деформаций в зависимости от состояния металла и приращения нагрузки. Критерий текучести металла является скалярной функцией напряжений и внутренних переменных и задается общей функцией 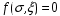 , (1.14) , (1.14)где ξ – функция, зависящая от истории нагружения, скалярных и тензорных внутренних переменных. Таким образом, уравнение (1.14) описывает условие перехода из зоны упругих деформаций в зону пластических. Развитие пластических деформаций определяется законом 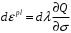 . (1.15) . (1.15)где 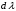 – величинa приращения пластической деформации; – величинa приращения пластической деформации; 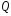 – пластический потенциал. – пластический потенциал.Критерий текучести для большинства металлов зависит от истории нагружения и изменения пластических деформаций. Изменение критерия текучести при повышении нагрузки называется упрочнением и определяется правилом упрочнения. Наиболее применимыми для металлов являются два правила упрочнения: изотропное и кинематическое упрочнение. Для изотропного упрочнения поверхность текучести задается уравнением 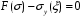 , (1.16) , (1.16)где 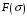 – скалярная функция напряжений, определяющая предел текучести металла. – скалярная функция напряжений, определяющая предел текучести металла.Этот тип упрочнения может моделировать поведение металлов при монотонном нагружении и упругой разгрузке, но часто не дает хорошие результаты для структур, которые испытывают пластическую деформацию после изменения направления нагрузки на противоположное. Для кинематического упрочнения поверхность текучести имеет другую форму 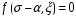 , (1.17) , (1.17)где 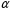 – тензор обратных напряжений. – тензор обратных напряжений.В программе ANSYS доступны три общих класса изотропных моделей упрочнения: билинейная, полилинейная и нелинейная. Каждая из моделей упрочнения предполагает критерий текучести Мизеса для изотропных свойств материалов. Критерий текучести Мизеса обычно используется в моделях пластичности для широкого спектра металлов 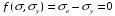 , (1.18) , (1.18)где σе – эквивалентные напряжения фон Мизеса 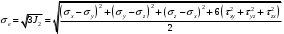 , (1.19) , (1.19)где 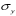 – предел текучести, соответствующий одноосному нагружению; – предел текучести, соответствующий одноосному нагружению;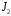 – второй инвариант девиатора напряжений. – второй инвариант девиатора напряжений.Билинейное изотропное упрочнение описывается билинейной обобщенной диаграммой 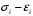 (см. рисунок 1.2). (см. рисунок 1.2).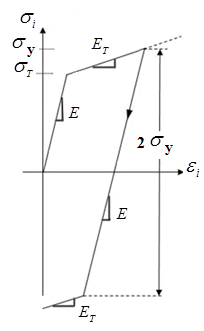 Рисунок 1.2 Диаграмма  для билинейного изотропного упрочнения для билинейного изотропного упрочненияПолилинейное упрочнение описывается кусочно-линейными напряжениями на обобщенной кривой деформаций, начиная с начала координат, и определяется табличными наборами значений положительных напряжений и деформаций, как показано на рисунке 1.3. 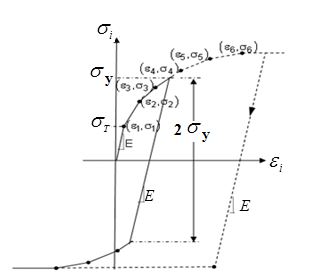 Рисунок 1.3 Диаграмма  для мультилинейного изотропного упрочнения для мультилинейного изотропного упрочненияДля нелинейной модели изотропного упрочнения применяется описание обобщенной кривой деформирования в области пластических деформаций с помощью степенной функции. Уравнение степенного закона имеет начальный предел текучести 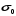 и показатель степени N, определенные пользователем. Текущий предел текучести и показатель степени N, определенные пользователем. Текущий предел текучести 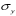 определяется решением следующего уравнения: определяется решением следующего уравнения: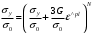 , (1.20) , (1.20)где 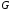 ˗ модуль сдвига, определяемый по заданным упругим постоянным: модулю упругости ˗ модуль сдвига, определяемый по заданным упругим постоянным: модулю упругости 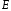 и коэффициенту Пуассона и коэффициенту Пуассона 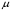 ; ;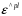 – накопленная эквивалентная пластическая деформация. – накопленная эквивалентная пластическая деформация.АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ ТРУБОПРОВОДА 2.1 Определение кольцевых и продольных напряжений горизонтальной трубы круглого сечения Программа ANSYS позволяет решать целый комплекс всевозможных задач из различных направлений не только механики, но и других физических дисциплин. При открытии программы с левой стороны можно увидеть длинный список задач, которые она может решать. В данной работе будут рассмотрены только две задачи, относящиеся к механике твердого тела и, соответственно, расчету реальных строительных конструкций. В основном, будет использоваться режим Static Structural, предназначенный для решения зада напряженно-деформированного состояния твердых тел. На рисунке 2.1 можно увидеть список возможных режимов работы, а также главное окно проекта в режиме Static Structural. 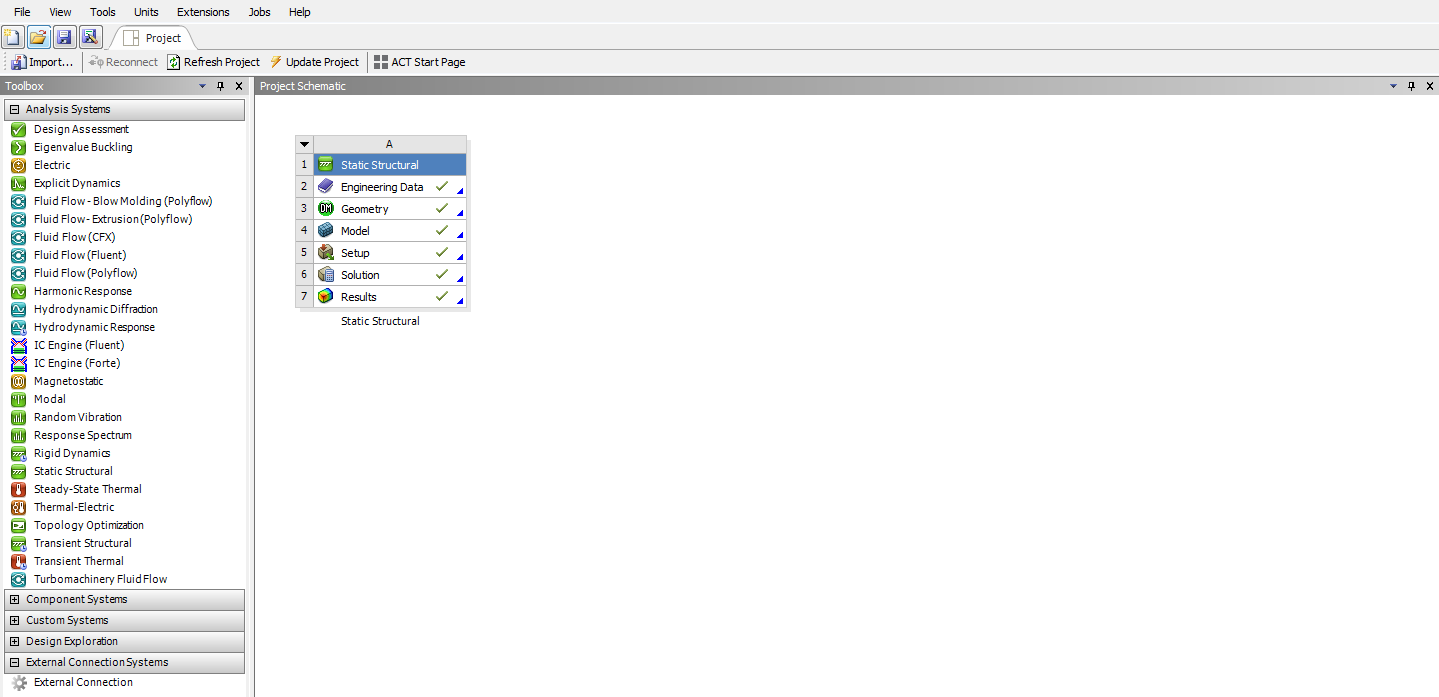 Рисунок 2.1 Окно проекта в режиме Static Structural Во вкладке Geometry создаем новую область геометрической модели, для этого кликаем по вкладке правой кнопкой мыши и выбираем команду New DesignModeler Geometry. Открывается рабочая область геометрической модели, в левой части которой показано дерево геометрической модели. Здесь отображаются все рабочие плоскости, эскизы, выполненные команды и построенные объекты. Для начала в самой верхней строке заходим в Units выбираем там в качестве единицы измерения миллиметры, после чего регулируем масштаб области моделирования. Заходим в самую первую плоскость XYPlane и с помощью специального значка в верхней панели создаем новый эскиз – Sketch1. Поворачиваем к нам рабочую плоскость и переходим из дерева модели в режим Sketching, предназначенный для построения эскизов на плоскости из набора простых фигур и специальных инструментов. Во вкладке Draw представлены все основные геометрические формы, которыми располагает программа. Выбираем Circular и строим две окружности с центром в начале координат. Таким образом, мы построили поперечное сечение трубы. Далее задаемся геометрическими размерами трубы. Принимаем наружный диаметр трубы равным Dн = 350 мм, а толщину стенки δ = 7 мм. Тогда внутренний диаметр трубы рассчитаем по формуле: Dвн = Dн - 2δ = 350 - 2 · 7 = 326 мм. (2.1) Во вкладке Dimensions задаем размеры окружностей. По умолчанию выбирается General – это основной размер фигуры. Для окружности основным размером является диаметр. На рисунке 2.2 показан эскиз сечения трубы с заданными размерами. 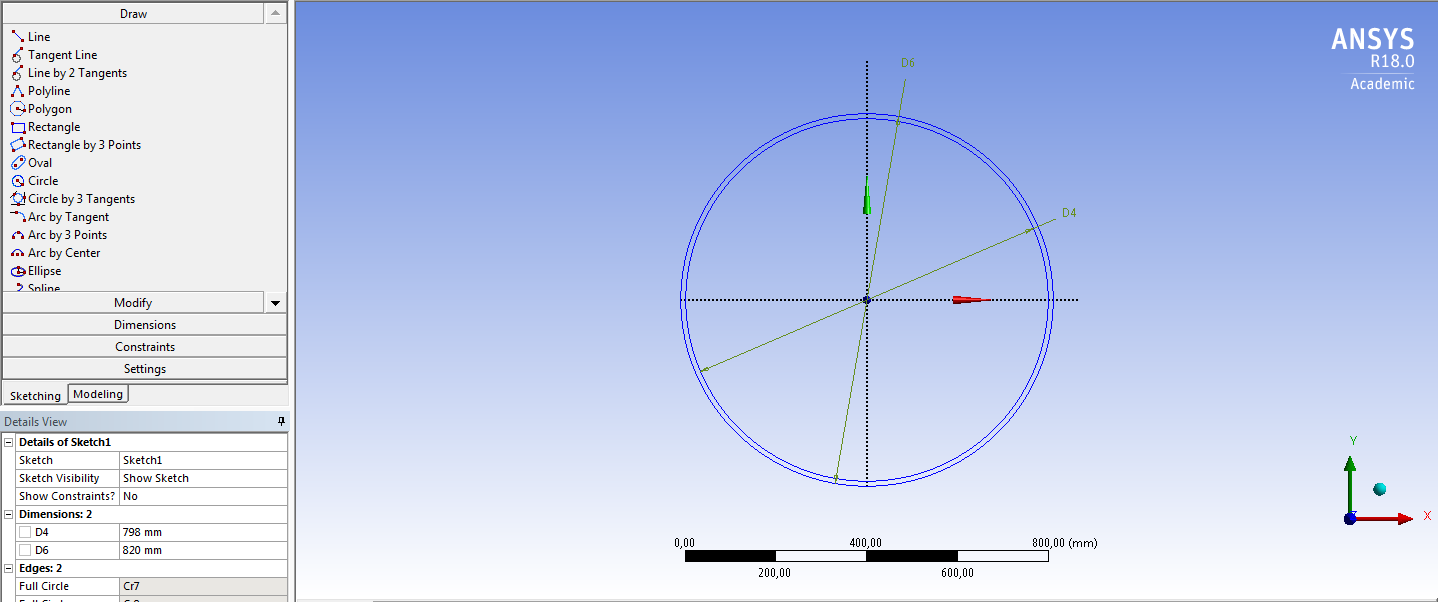 Рисунок 2.2 Эскиз поперечного сечения трубы Переходим обратно в режим Modeling, где выбираем инструмент Extrude, с помощью которого можно вытянуть выбранный эскиз на заданную величину в выбранном направлении. Как правило, направление задается по умолчанию – нормально к плоскости эскиза. Примем длину трубы равнойl = 10 м, поэтому величину вытягивания задаем равной 10000 мм. На рисунке 2.3 показан результат выполнения данной команды. 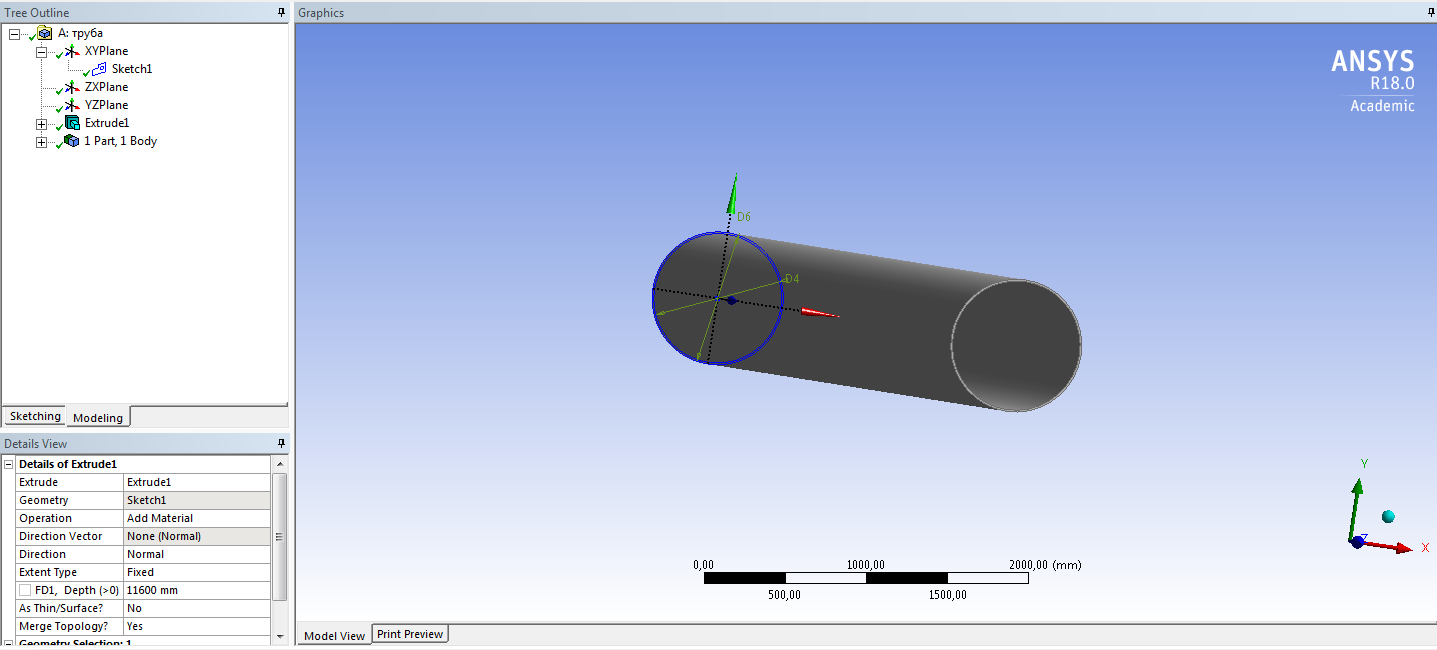 Рисунок 2.3 Геометрическая модель трубы После построения геометрической модели возвращаемся в основное окно проекта и переходим на следующий этап – Model. На данном этапе строится сетка конечных элементов модели. Выполняем команду Generate Mesh. Если полученная сетка вышла слишком плотной, это может затруднить расчет. В случае простой модели, для которой нет необходимости делать сетку слишком точной, как в нашем случае, можно отрегулировать величину элементов сетки. Для этого в области Details of “Mesh” в строке Element Size задаем минимальное значение величины элемента сетки. Принимаем для нашей модели 0,2 м. На рисунке 2.4 можно увидеть результат. 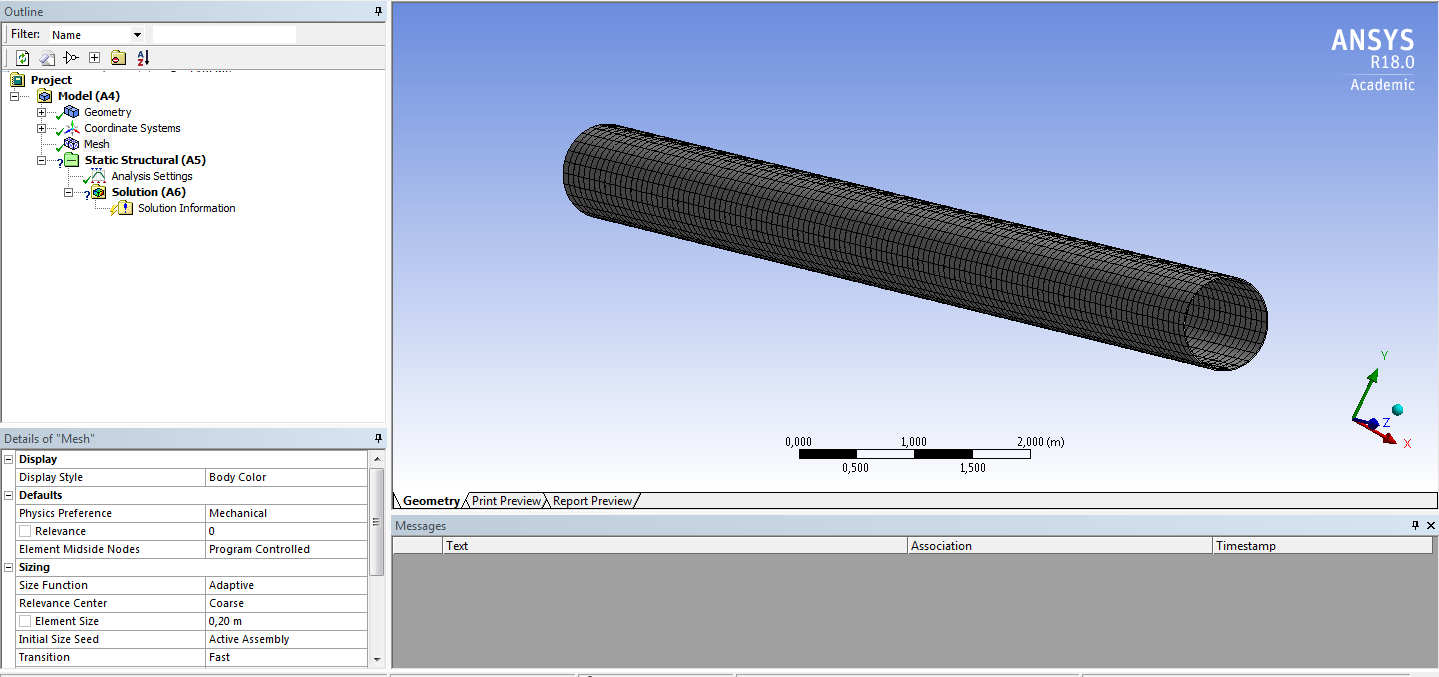 Рисунок 2.4 Сетка конечных элементов модели Следующим этапом является определение граничных условий и картины нагружения конструкции в разделе Setup. Граничные условия определяются тем, что труба должна быть жестко заделана с обеих сторон, то есть крайние сечения трубы не должны никак перемещаться. Для такой цели используется команда Fixed Support – это жесткая заделка, которая прикладывается в данном случае к крайнему кольцевому сечению трубы. Так как зафиксировать трубу нужно с обеих сторон, заделку прикладываем дважды сначала с одного, потом с другого края. На рисунке 2.5 показано, как выглядит жесткая заделка на геометрической модели.  Рисунок 2.5 Жесткая заделка крайних сечений трубы Нагружение трубы определяем без учета внешних нагрузок и собственного веса трубы, остается только внутреннее избыточное давление перекачиваемой среды. Давление на поверхность задается командой Pressure, в которой задается поверхность распределения давления и его величина. Принимаем одно из стандартных значений для напорного магистрального трубопровода Рраб= 6,4 МПа. На рисунке 2.6 показана картина нагружения внутренней полости трубы избыточным давлением продукта. 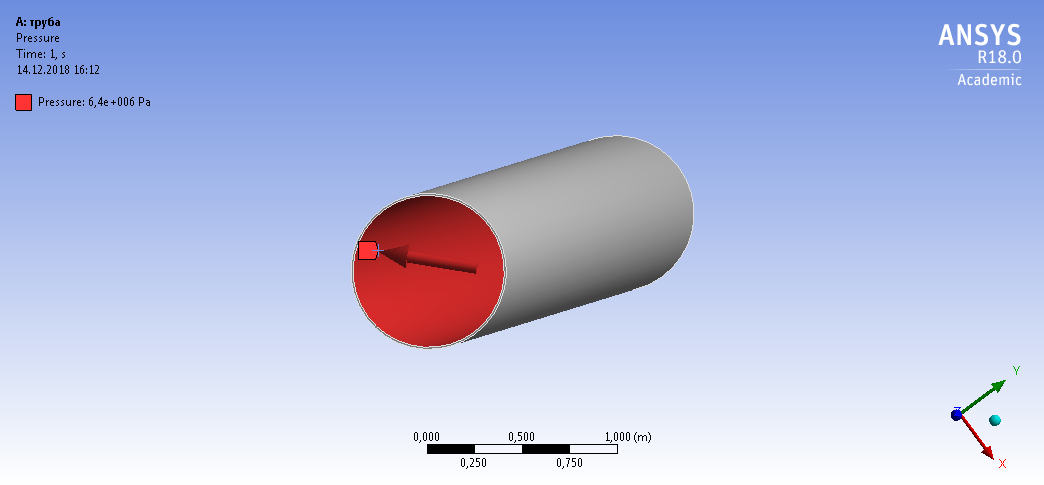 Рисунок 2.6 Нагружение трубы внутренним избыточным давлением Задав полностью все условия, в которых находится конструкция, переходим к расчету требуемых параметров. В задании необходимо получить значения кольцевых и продольных напряжений в трубе. Переходим к этапу Solution, где задаются параметры, которые необходимо рассчитать. Продольные напряжения действуют по всей поверхности трубы вдоль ее оси, в данном случае это напряжения вдоль оси Z. Кольцевые напряжения направлены по касательной к поверхности трубы в данной точке, их направление относительно базовой системы координат отличается, в таком случае необходимо определить напряжения вдоль оси X и выбрать образующую трубы, для которой направление кольцевых напряжений совпадет с осью X. Картину напряжений вдоль заданной оси можно получить при использовании команды Normal Stress. Дважды задаем эту команду и выбираем для кольцевых напряжений ось X, а для продольных – ось Z. Для точности определения кольцевых напряжений рассечем трубу плоскостью симметрии вдоль оси. На рисунке 2.7 показано несколько проб кольцевых напряжений в точках, лежащих на одной образующей. На рисунке 2.8 показано несколько проб для продольных напряжений. 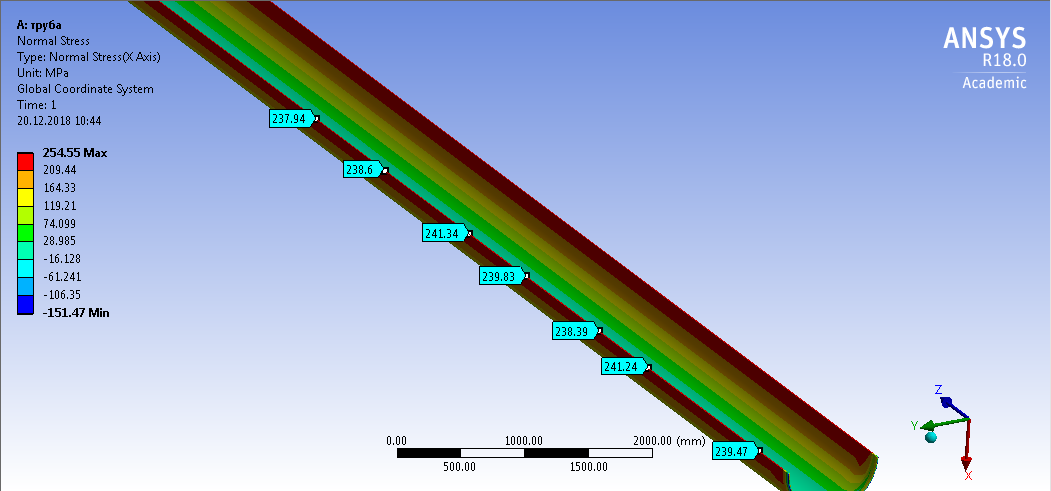 Рисунок 2.7 Кольцевые напряжения трубы 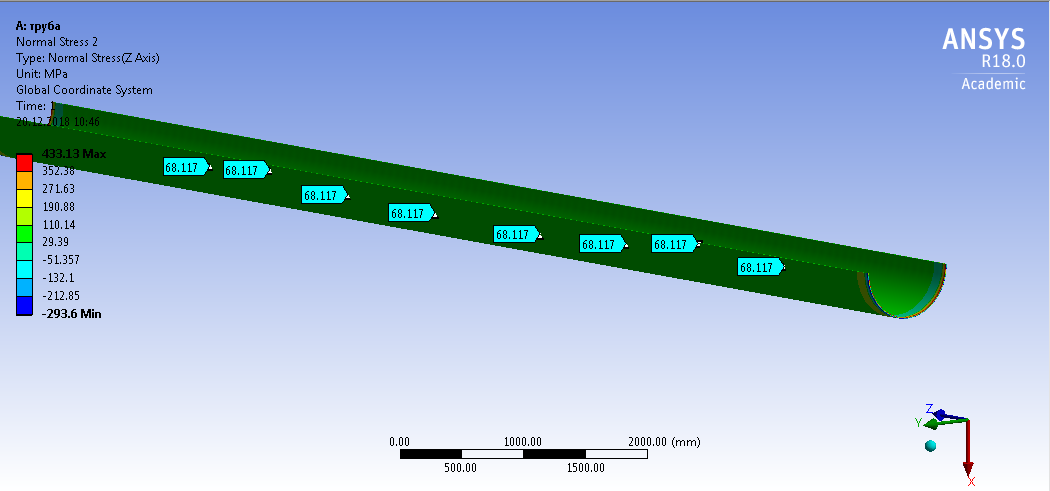 Рисунок 2.8 Продольные напряжения трубы Теоретическое значение кольцевых и продольных напряжений можно рассчитать по следующим формулам: 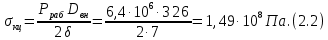 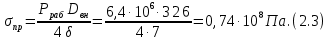 Сравнивая значения, полученные по формулам (2.2) и (2.3), с теми значениями, что были определены численным методом, мы видим, что кольцевые напряжения определяются с достаточной точностью, а вот погрешность при определении продольных напряжений получилась практически в два раза. 2.2 Моделирование П-образного компенсатора Заходим в главное окно программы и с помощью команды Dublicate копируем созданный проект. Даем новому проекту другое название и заходим в геометрию. Здесь поперечное сечение трубы можно оставить без изменений, а можно задать иные размеры трубы. Зададим теперь наружный диаметрDн = 530 мм, а толщину стенки оставим той же. Тогда внутренний диаметр трубы рассчитаем по формуле: Dвн = Dн - 2δ = 530 - 2 · 7 = 516 мм. (2.1.1) На рисунке 2.9 показан эскиз поперечного сечения П-образного компенсатора. 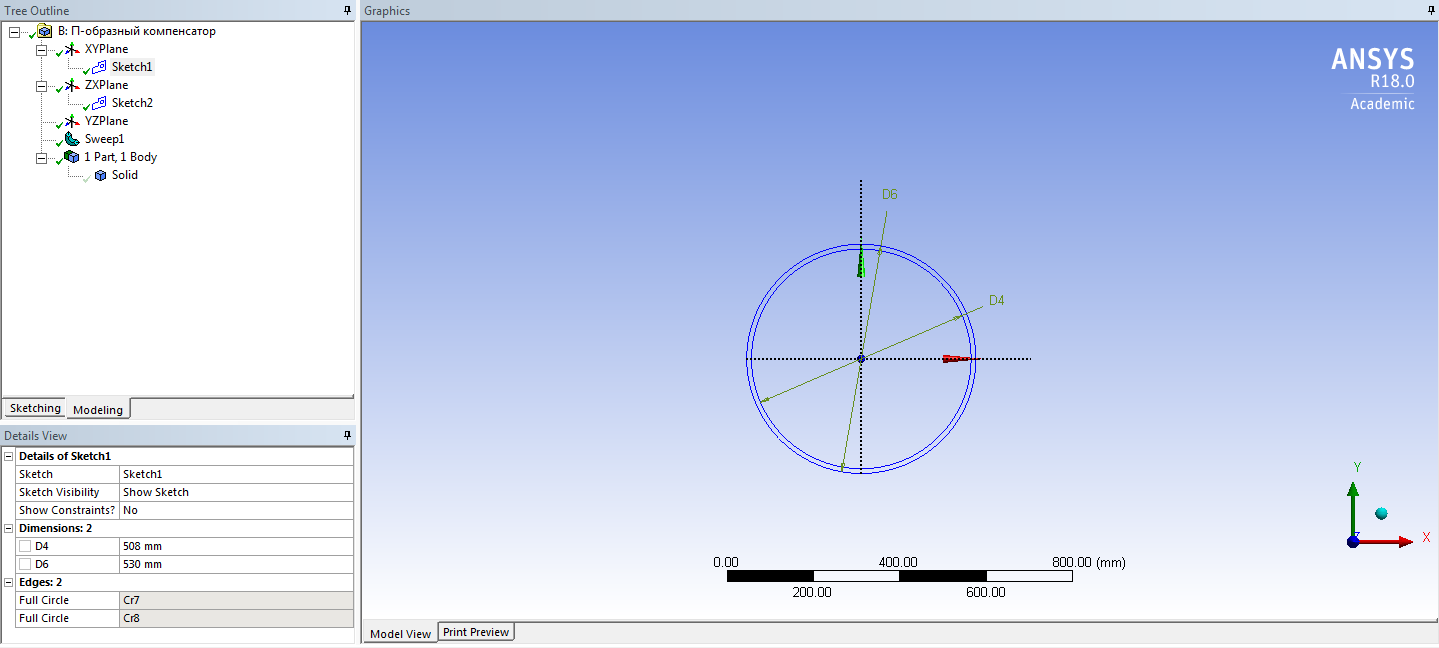 Рисунок 2.9 Эскиз поперечного сечения компенсатора Далее переходим в плоскость ZXPlane и создаем в ней новый эскиз – Sketch2, в котором построим траекторию, по которой будет изгибаться труба. Сначала в режиме Sketching во вкладке Draw выбираем инструмент Line и чертим каркас П-образного компенсатора. Далее с помощью команды Fillet во вкладке Modify задаем радиус скругления, равный 0,5 м, и скругляем все углы. Задаем все необходимые размеры: для П-образного компенсатора это радиус скругления Rк = 0,5 м, высота компенсатора lк = 8 м и величина пролета lп = 8 м. На рисунке 2.10 показан получившийся эскиз. 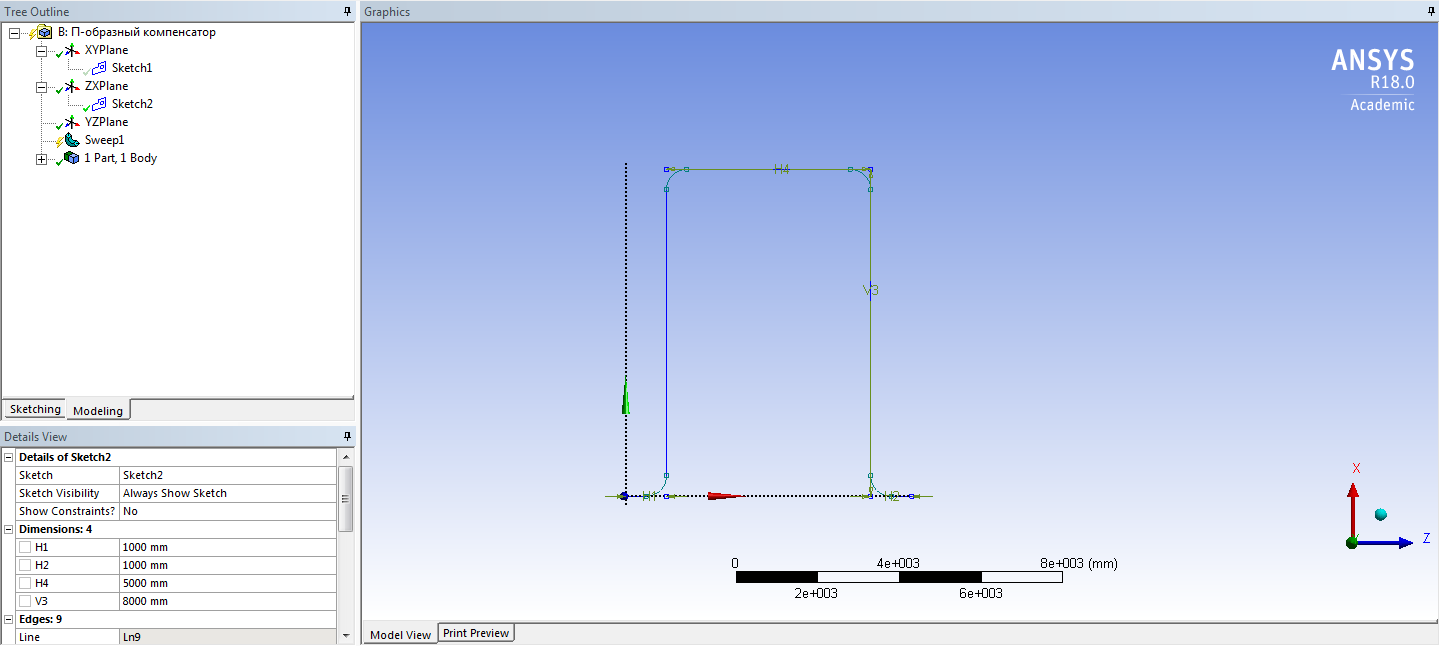 Рисунок 2.10 Эскиз линии изгиба компенсатора Команду Extrude удаляем, вместе с ней удалится и построенное ранее тело. Геометрическую модель компенсатора строим с помощью команды Sweep, для которой выбираем в качестве перемещаемой фигуры Sketch1, а в качестве траектории перемещения – Sketch2. Результат представлен на рисунке 2.11.  Рисунок 2.11 Геометрическая модель П-образного компенсатора Изменив геометрию модели, переходим на этап генерации сетки. Результат показан на рисунке 2.12. 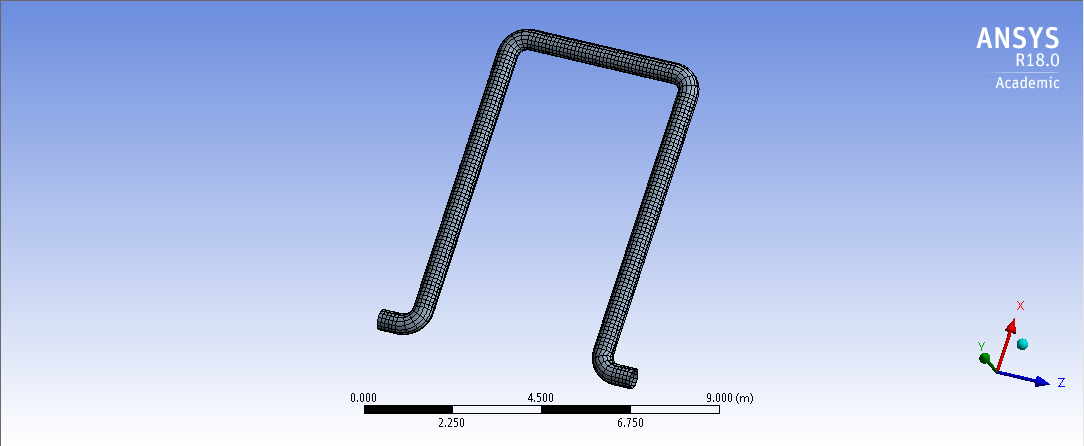 Рисунок 2.12 Сетка конечных элементов модели Задаем условия для расчетной модели. Одно крайнее сечение компенсатора зафиксируем так, чтобы все перемещения были равны нулю. К противоположному сечению необходимо приложить нагрузку, направленную перпендикулярно к нему в направлении сжатия. Фиксируем одно сечение с помощью Fixed Support, к другому сечению с помощью команды Force прикладываем нагрузку, равную Р = 10000 Н. На рисунке 2.13 показана полученная расчетная модель. 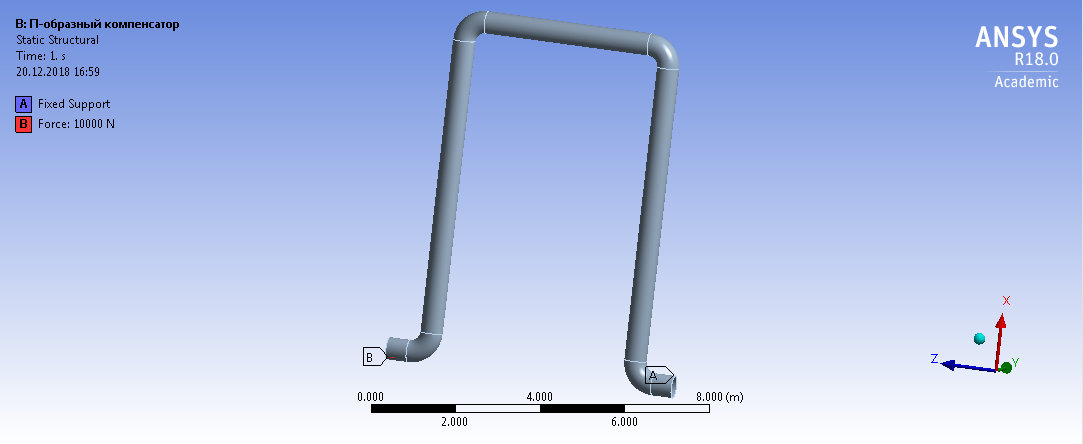 Рисунок 2.13 Расчетная модель П-образного компенсатора Определяем горизонтальные перемещения компенсатора с помощью команды Directional Deformation, задавая перемещения вдоль оси Z. На рисунке 2.14 показан результат расчета. 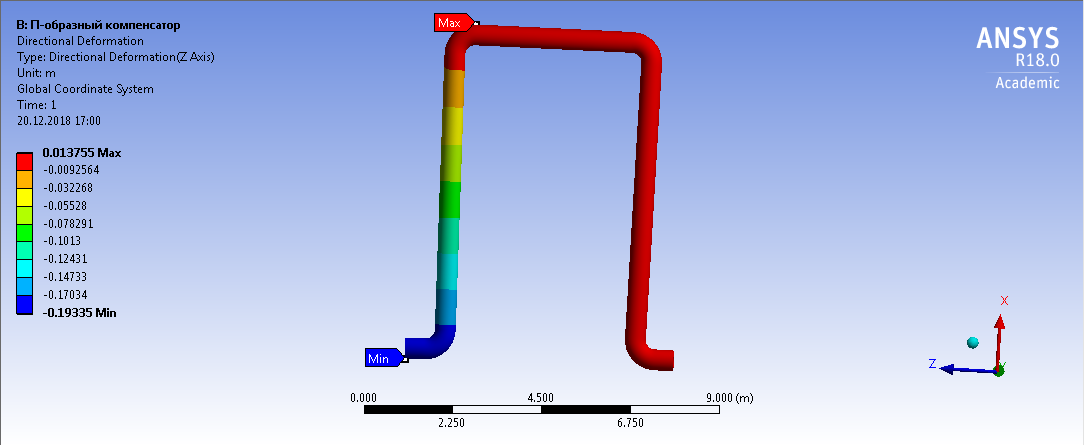 Рисунок 2.14 Горизонтальные перемещения П-образного компенсатора Рассчитаем податливость компенсатора при заданных условиях по известной формуле: 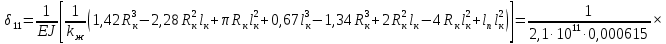 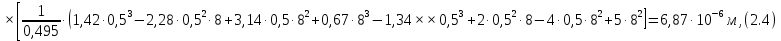 где EJ – жесткость компенсатора; kж – коэффициент снижения жесткости при изгибе, рассчитываемый по формуле: 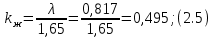 λ – геометрическая характеристика отвода: 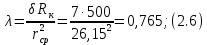 rср – средний радиус кольцевого сечения отвода, определяющийся следующим образом: 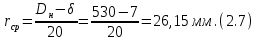 Жесткость компенсатора определяется модулем Юнга для стали E = 2,1·105 МПа и моментом инерции J, которое для кольцевого сечения определится по формуле: 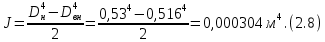 Так как податливость компенсатора есть перемещение его под действием единичной силы, перемещение под действующей нагрузкой определяем по пропорции: 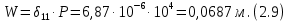 На рисунке 2.15 мы видим, что картина перемещений близка к действительности, однако расчетное значение сильно расходится с тем, что было получено численным методом – 0,193 м. Ввиду сложности формулы (2.4), погрешности могут быть достаточно велики при определенных параметрах. 2.3 Моделирование Z-образного компенсатора Снова создаем копию последнего проекта. Поперечное сечение трубы оставляем без изменения, а конфигурацию компенсатора изменяем, удаляя лишние элементы и задавая новые размеры. Принимаем l1 = l2 = 4 м, lк = 5 м. Полученный эскиз линии изгиба компенсатора показан на рисунке 2.15. Команда Sweep остается заданной тем же образом. Обновим модель, нажав на Generate и получим геометрическую модель Z-образного компенсатора, показанную на рисунке 2.16. 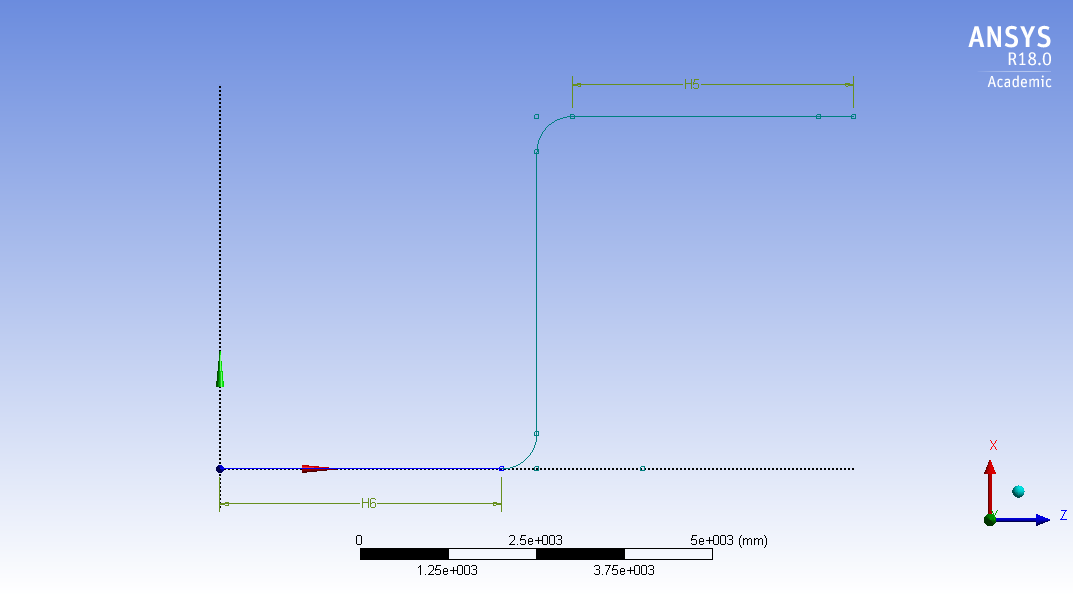 Рисунок 2.15 Эскиз линии изгиба Z-образного компенсатора  Рисунок 2.16 Геометрическая модель Z-образного компенсатора Далее задаем аналогичным образом граничные условия и нагрузки (см. рис. 2.17) и обновляем расчет командой Solve. На рисунке 2.18 можно увидеть результат расчета горизонтальных перемещений. 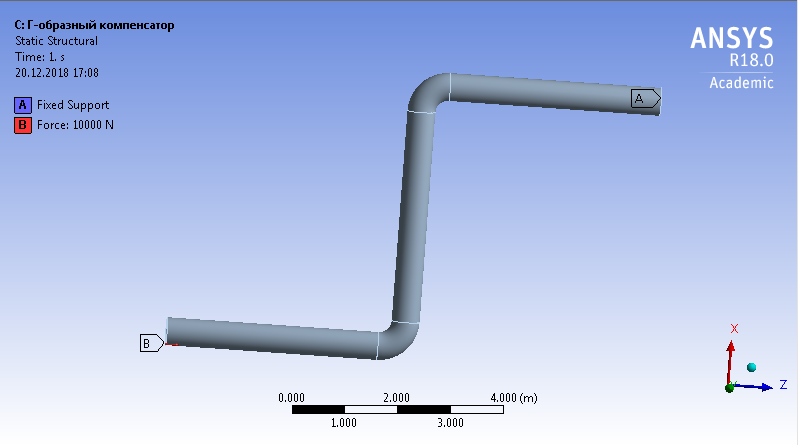 Рисунок 2.17 Расчетная модель Z-образного компенсатора  Рисунок 2.18 Расчет горизонтальных перемещений Определим податливость компенсатора по известной формуле: 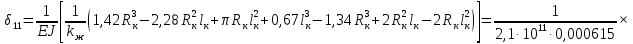 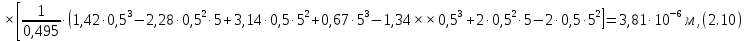 Перемещение под действием фактической нагрузки определяем по формуле (2.9): 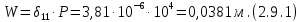 Сравниваем полученный результат с результатом по методу конечных элементов – 0,024 м. Погрешность для данного расчета уже меньше, но все еще достаточно велика. ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ РВС 3.1 Построение геометрической модели резервуараЧтобы построить геометрическую модель стенки и днища резервуара, воспользуемся командой Revolve, которая осуществляет построение тел вращения поворотом на определенный угол вокруг заданной оси эскизного рисунка на плоскости. Переходим в плоскость XYPlane и создаем в ней несколько эскизов. Стенка резервуара будет сложена из четырех поясов. Таким образом, создаем 5 эскизов: для каждого пояса стенки резервуара и для его днища. Высоту пояса принимаем равной 1,5 м. Высота стенки резервуара в таком случае будет равна 6 м. Радиус вертикального резервуара принимаем равным 8 м, радиус днища с добавлением окрайки – 8,2 м. С помощью инструмента Line во вкладке Draw режима Sketching чертим образующие днища и поясов стенки резервуара. Во вкладке Demensions выбираем General и наносим основные размеры резервуара: радиус днища и высоту каждого пояса. Радиус самого резервуара определяем с помощью инструмента Horisontal как расстояние от нижней точки самого нижнего пояса до вертикальной оси. На рисунке 3.1 показан получившийся эскиз образующих конструкции. 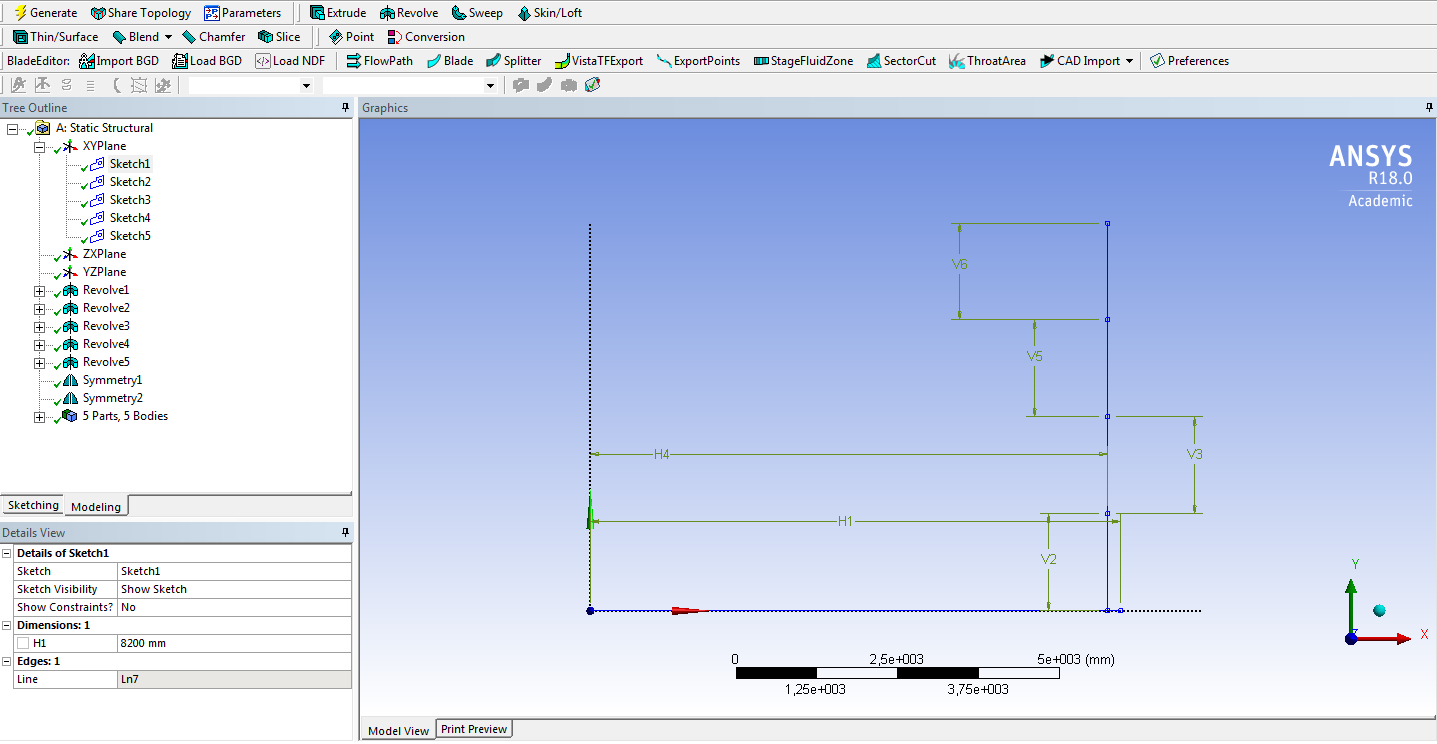 Рисунок 3.1 Эскиз образующих резервуара Для каждого эскиза выполняем команду Revolve, задавая в области редактирования параметров Details View в качестве оси вращения ось Y, угол поворота оставляем по умолчанию 360°, так как необходимо получить замкнутую поверхность. В качестве образующих выбираем соответствующие эскизы. Чтобы получить поверхность вращения с полостью внутри, необходимо в строке As Thin/Surface? выбрать Yes. Задав необходимые параметры, выбираем команду Generate и получаем геометрическую модель вертикального стального резервуара без крыши с днищем (см. рис. 3.2). 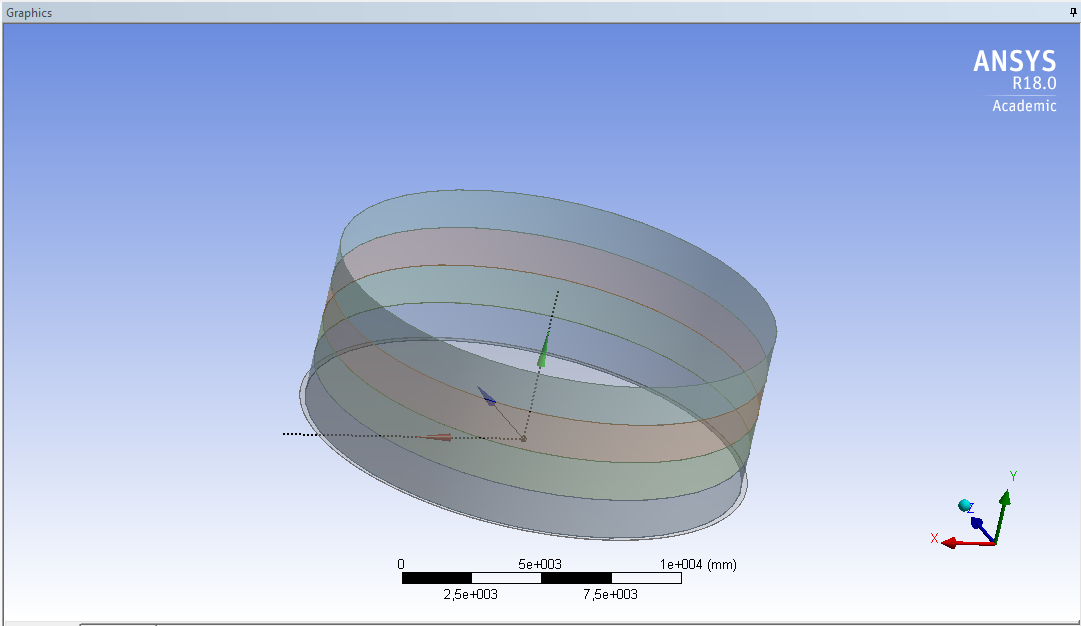 Рисунок 3.2 Геометрическая модель РВС Так как конструкция симметрична относительно вертикальной оси и нагружена равномерно, то достаточно рассмотреть только часть конструкции, полученную рассечением резервуара взаимно перпендикулярными плоскостями, проходящими через ось Y. Для того, чтобы рассечь конструкцию, выбираем команду Simmetry и указываем плоскость симметрии. Таким образом, получаем конструкцию, показанную на рисунке 3.3. Количество конечных элементов такой модели будет в 4 раза меньше, а значит, расчеты можно будет произвести в 4 раза быстрее. Либо, потратив столько же времени, увеличить точность расчета уменьшением размера конечного элемента в 4 раза. 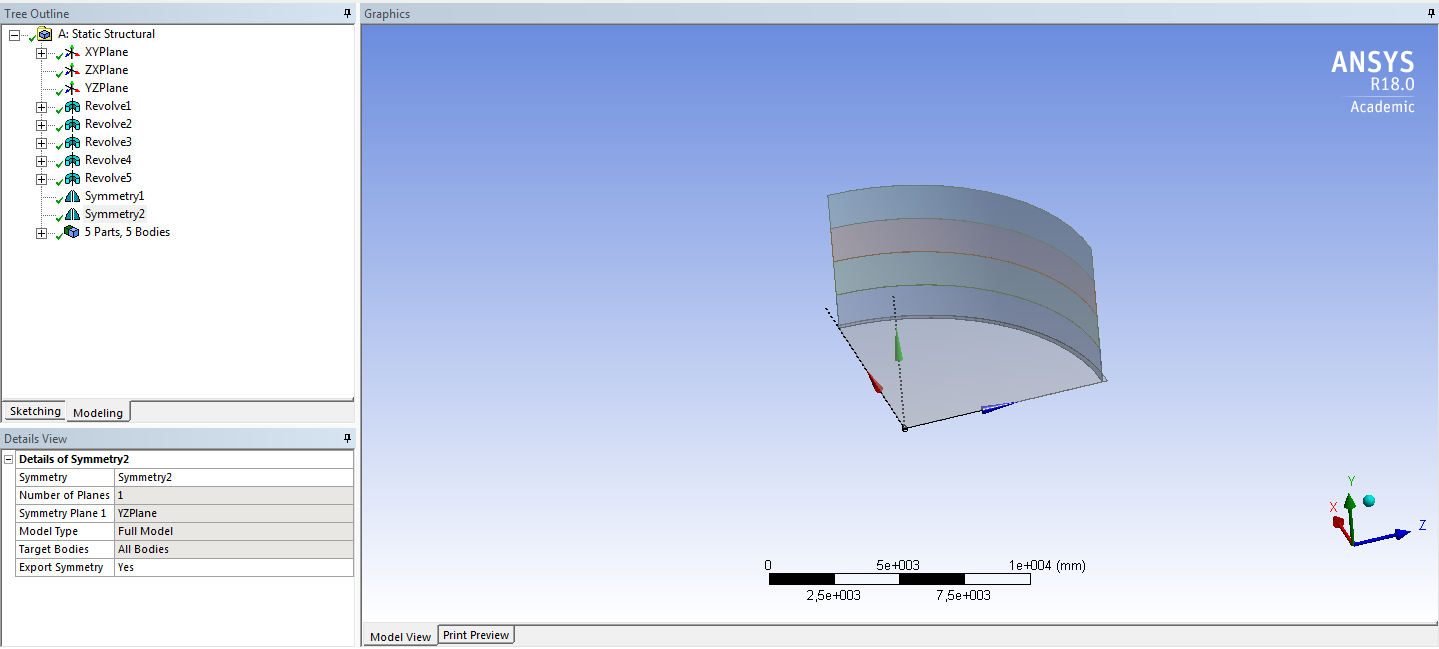 Рисунок 3.3 Рассечение модели плоскостями симметрии 3.2 Моделирование напряженно-деформированного состоянияПосле построения геометрии конструкции генерируем сетку конечных элементов. Для этого необходимо зайти во вкладку Mesh и выполнить в ней команду Generate Mesh. Результат показан на рисунке 3.4. 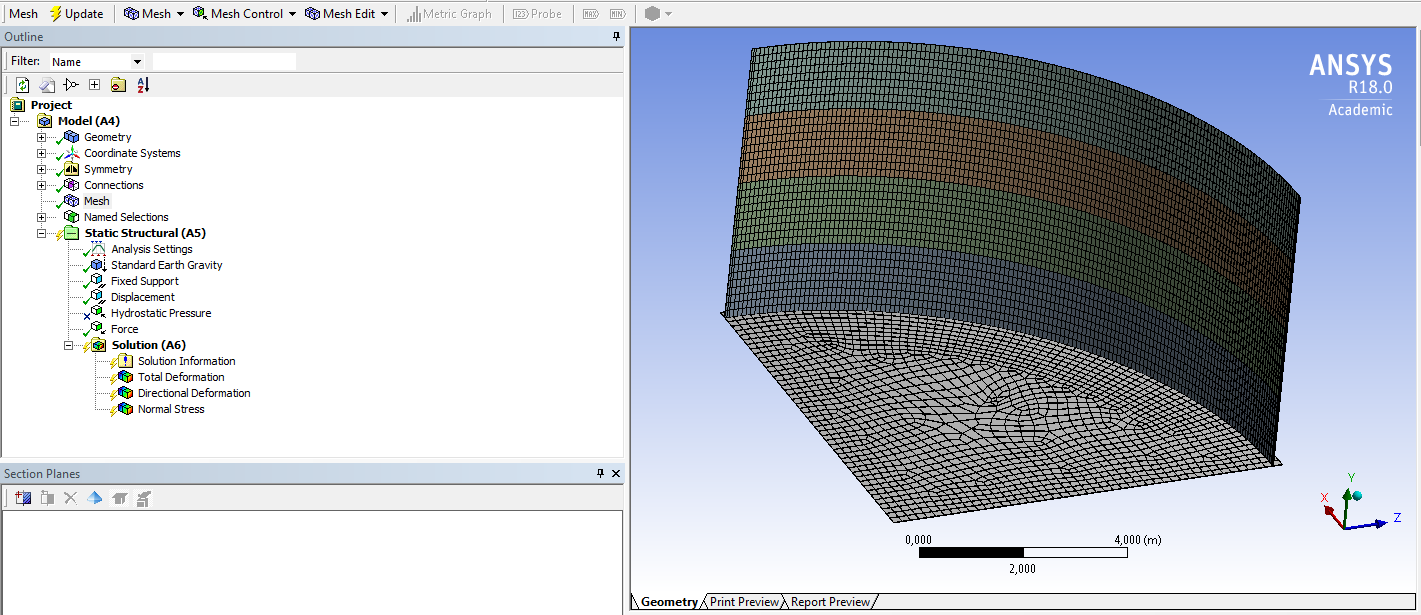 Рисунок 3.4 Сетка конечных элементов конструкции Определяем граничные условия для нашей модели, ограничивая перемещения для крайних сечений конструкции. К нижней поверхности днища резервуара прикладываем жесткую заделку – Fixed Support (см. рис. 3.5), а к верхнему контуру стенки, куда крепится крыша резервуара, прикладываем ограничения на линейные перемещения в горизонтальной плоскости (см. рис. 3.6). 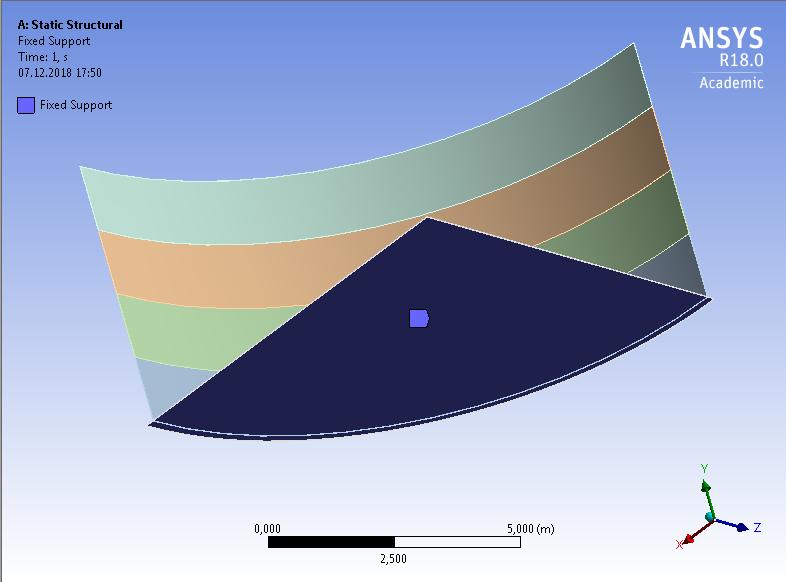 Рисунок 3.5 Жесткая заделка основания резервуара 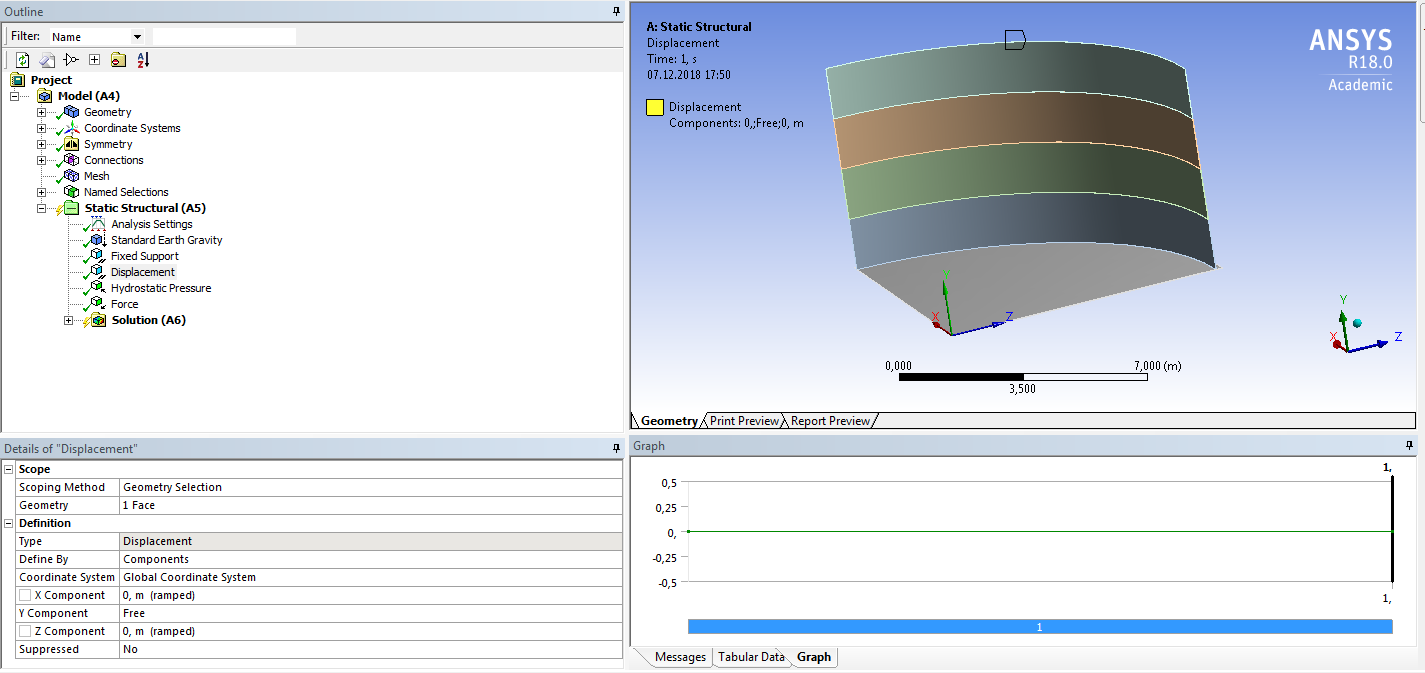 Рисунок 3.6 Ограничение перемещений в горизонтальной плоскости в месте крепления крыши резервуара Задаем нагрузки на резервуар. На рисунке 3.7 показано нагружение конструкции собственным весом наложением поля сил тяготения – Standard Earth Gravity. На рисунке 3.8 приложено гидростатическое давление столба жидкости внутри резервуара с помощью команды Hydrostatic Pressure. Для этого в области Details View задаем величину плотности жидкости, ускорения свободного падения и высоту наполнения резервуара. Сверху к стенке резервуара прикладываем нагрузку, передаваемую от крыши, в виде вертикальной силы, действующей в отрицательном направлении на стенку (см. рис. 3.9). Общая картина нагружения представлена на рисунке 3.10. 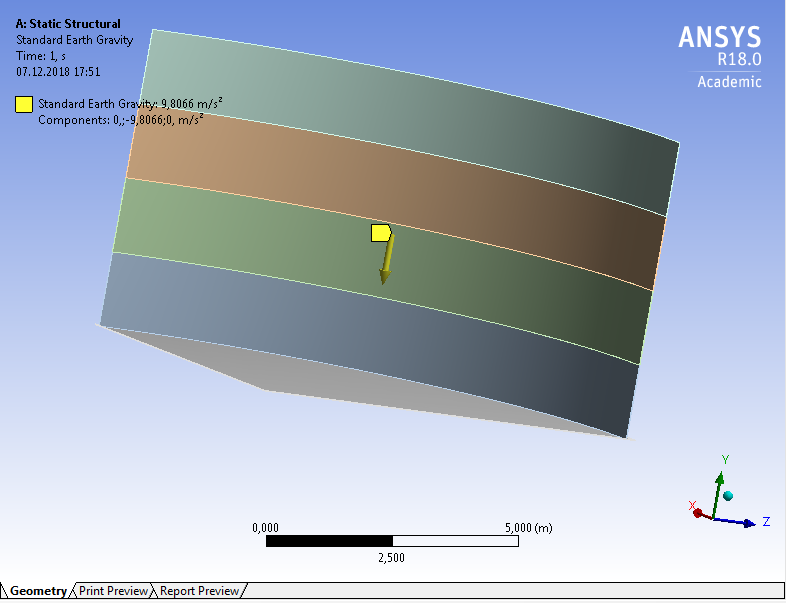 Рисунок 3.7 Приложение гравитационного поля 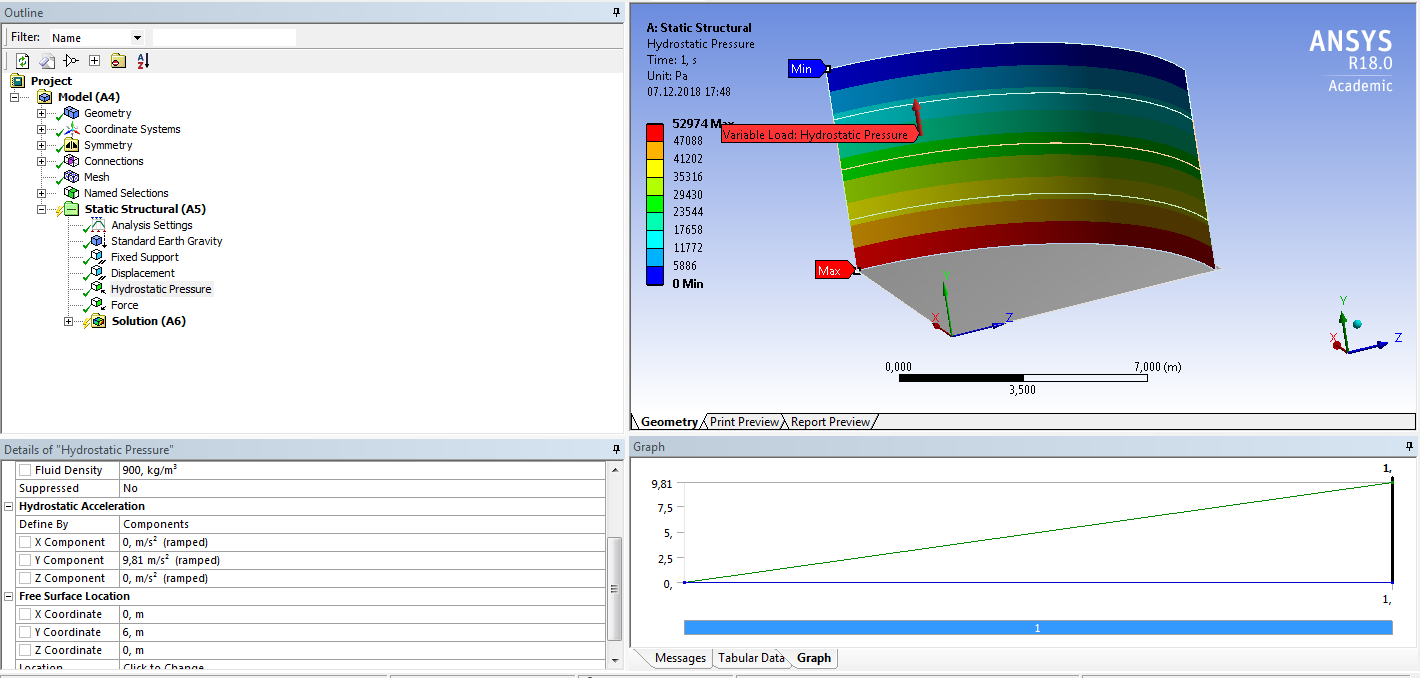 Рисунок 3.8 Нагружение РВС гидростатическим давлением 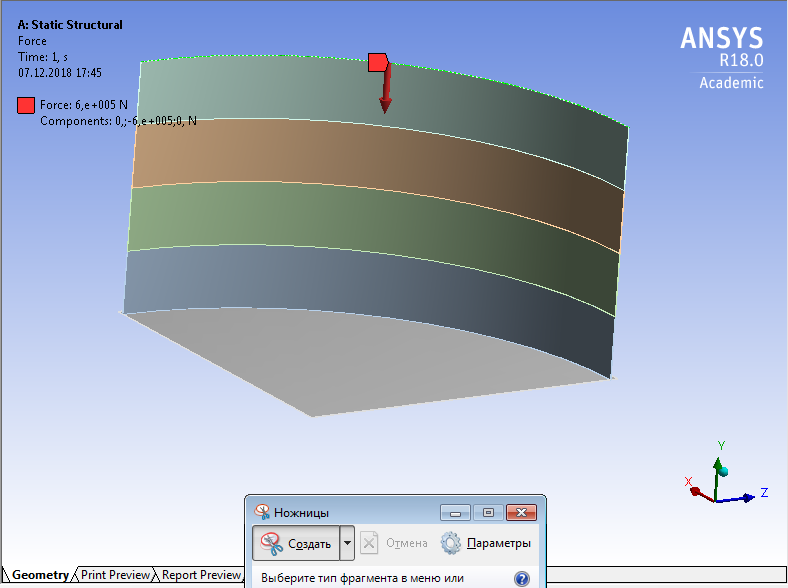 Рисунок 3.9 Нагрузка от крыши к стенке резервуара 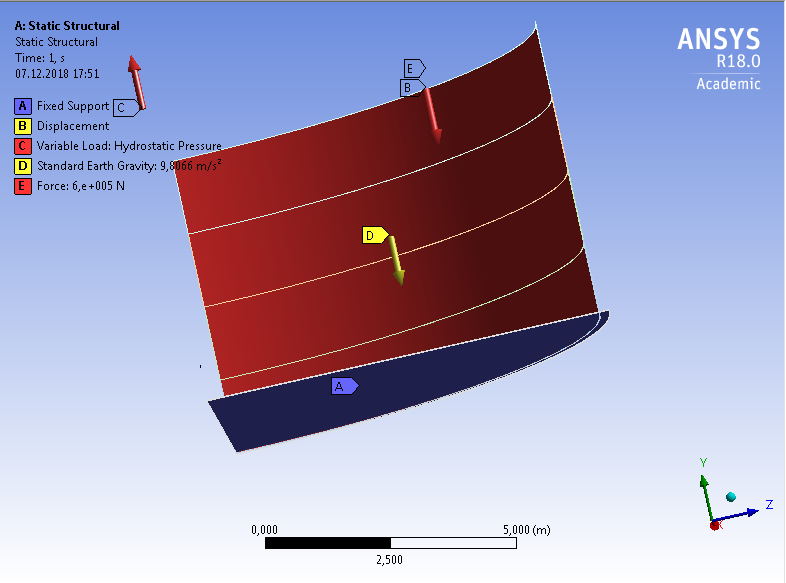 Рисунок 3.10 Расчетная модель РВС Рассчитываем полученную модель, задавая во вкладке Solution дерева модели параметры, которые хотим рассчитать. Распределение общих деформаций получаем с помощью команды Total Deformation (см. рис. 3.11). Для получения картины радиальных и кольцевых перемещений стенки резервуара, используем команду Directional Deformation, задавая в ней перемещения по оси X (см. рис. 3.12). Командой Normal Stress, задавая в ней ось Y, определяем вертикальные напряжения в стенке резервуара (см. рис. 3.13). 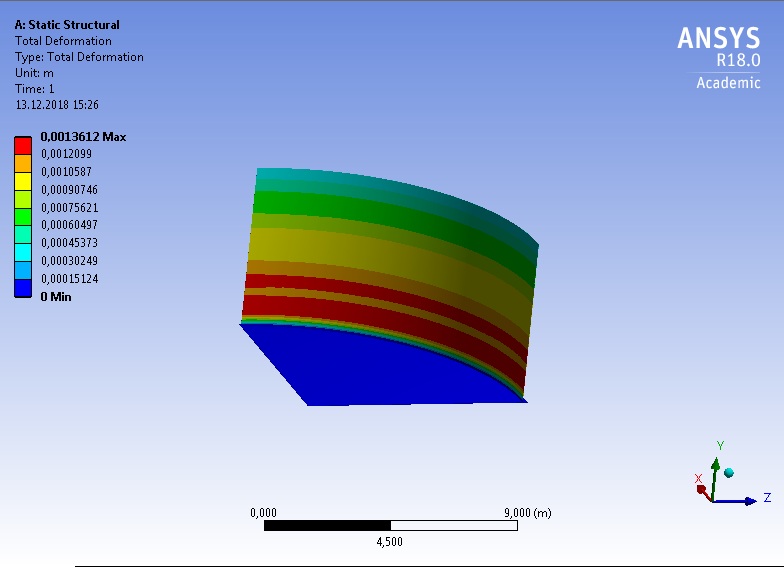 Рисунок 3.11 Определение общих деформаций стенки резервуара 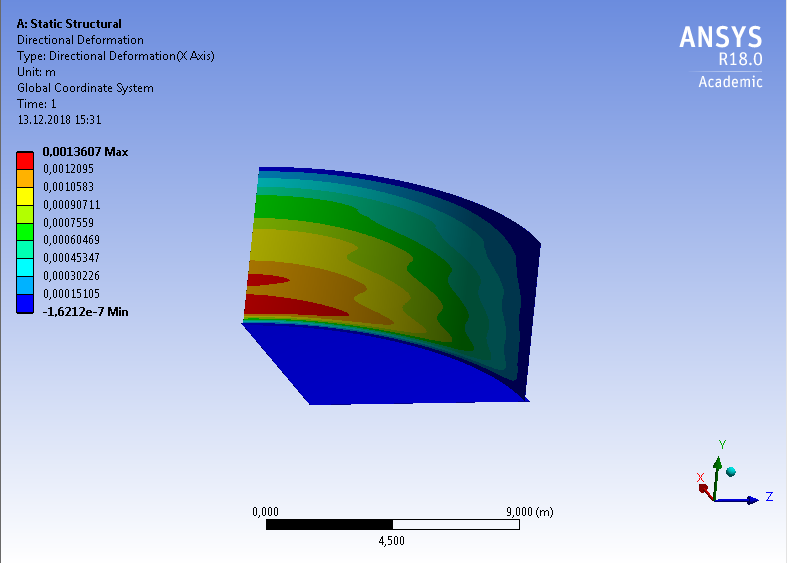 Рисунок 3.12 Определение радиальных и кольцевых деформаций стенки резервуара 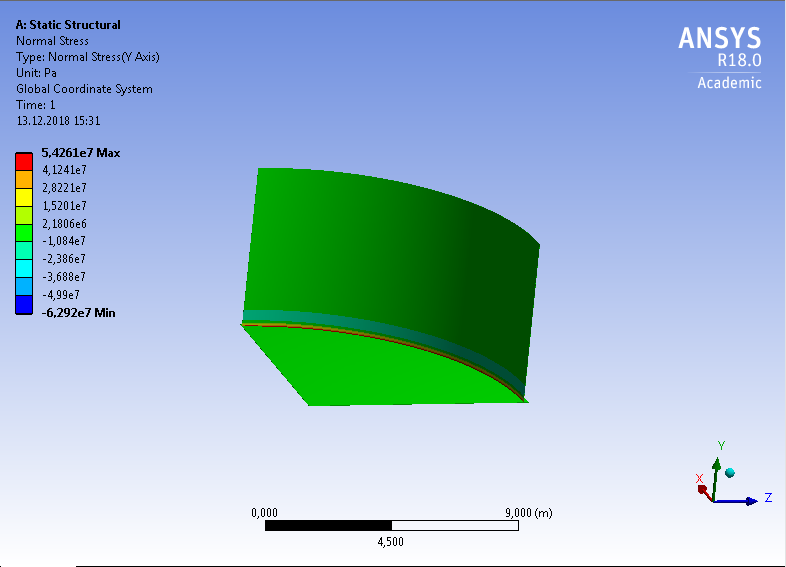 Рисунок 3.13 Определение вертикальных напряжений стенки резервуара 3.3 Моделирование вертикального резервуара на грунтовой подушке и построение диаграммы радиальных перемещенийВ плоскости XYPlane создаем новый эскиз, переходим в Sketching и с помощью инструмента Rectangle чертим сечение песчаного фундамента резервуара. Определяем его габаритные размеры и размещаем его с помощью инструмента Simmetry симметрично относительно вертикальной оси (см. рис. 3.14). 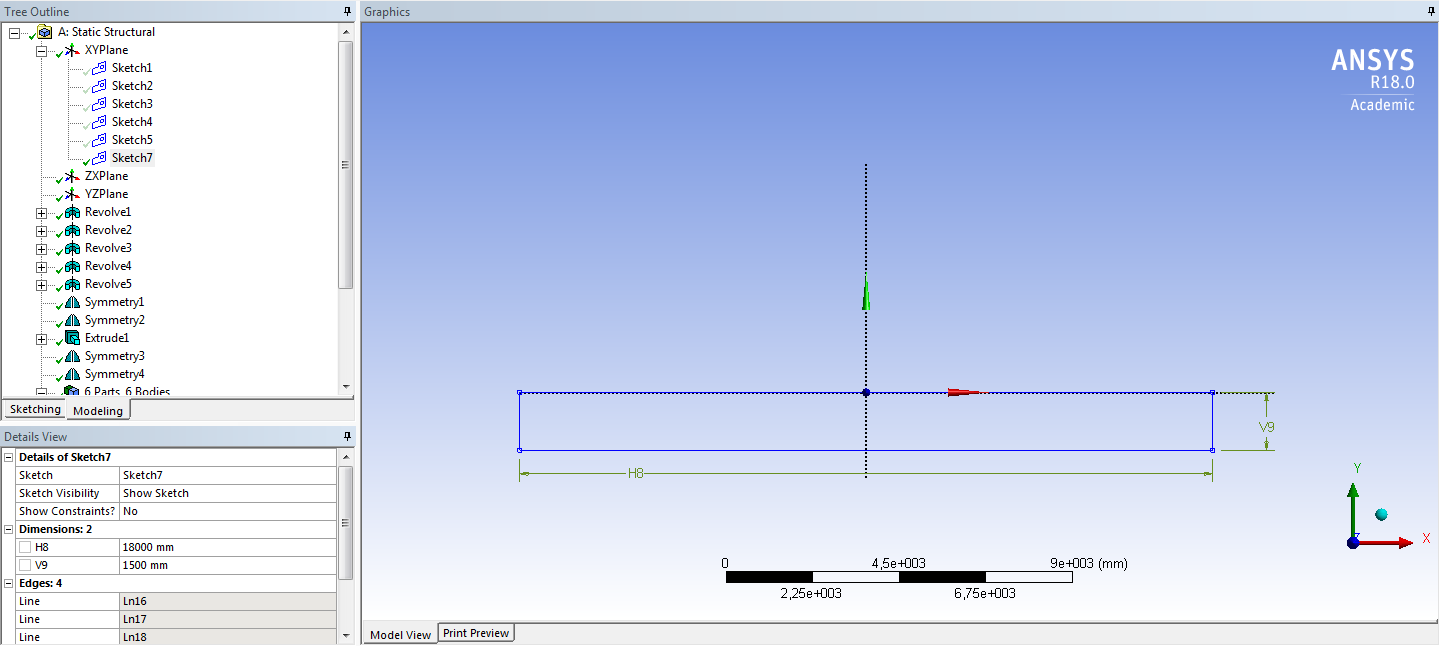 Рисунок 3.14 Эскиз песчаного фундамента Переходим в Modeling и командой Extrude вытягиваем фигуру в обе стороны на равное расстояние от плоскости XYPlane. Используем команду Simmetry для того чтобы разрезать фундамент по аналогии со стенкой резервуара. Фундамент резервуара необходимо выполнить из грунта. Так как по умолчанию для него будет задана сталь, необходимо зайти в редактирование свойств объекта и выбрать другой материал, который заранее необходимо добавить во вкладке Engineering Data главного окна проекта. Более подробно этап работы с материалами показан для шарового резервуара. После того, как материал фундамента изменен, переходим в модель и создаем сетку конечных элементов. Начальный вид сетки показан на рисунке 3.15.  Рисунок 3.15 Сетка конечных элементов, построенная по умолчанию На рисунке 3.15 мы видим, что полученная сетка очень точно передаст картину нагружения, но сильно замедлит расчет. Сделаем конечные элементы более крупными, чтобы уменьшить количество узлов и упростить расчет. Для этого заходим в Mesh и в области Details of “Mesh” в строке Element Size ставим размер, к примеру, 350 мм. Так как сетка уже сгенерирована, выполняем команду Update. Сетка приобретает вид, показанный на рисунке 3.16. 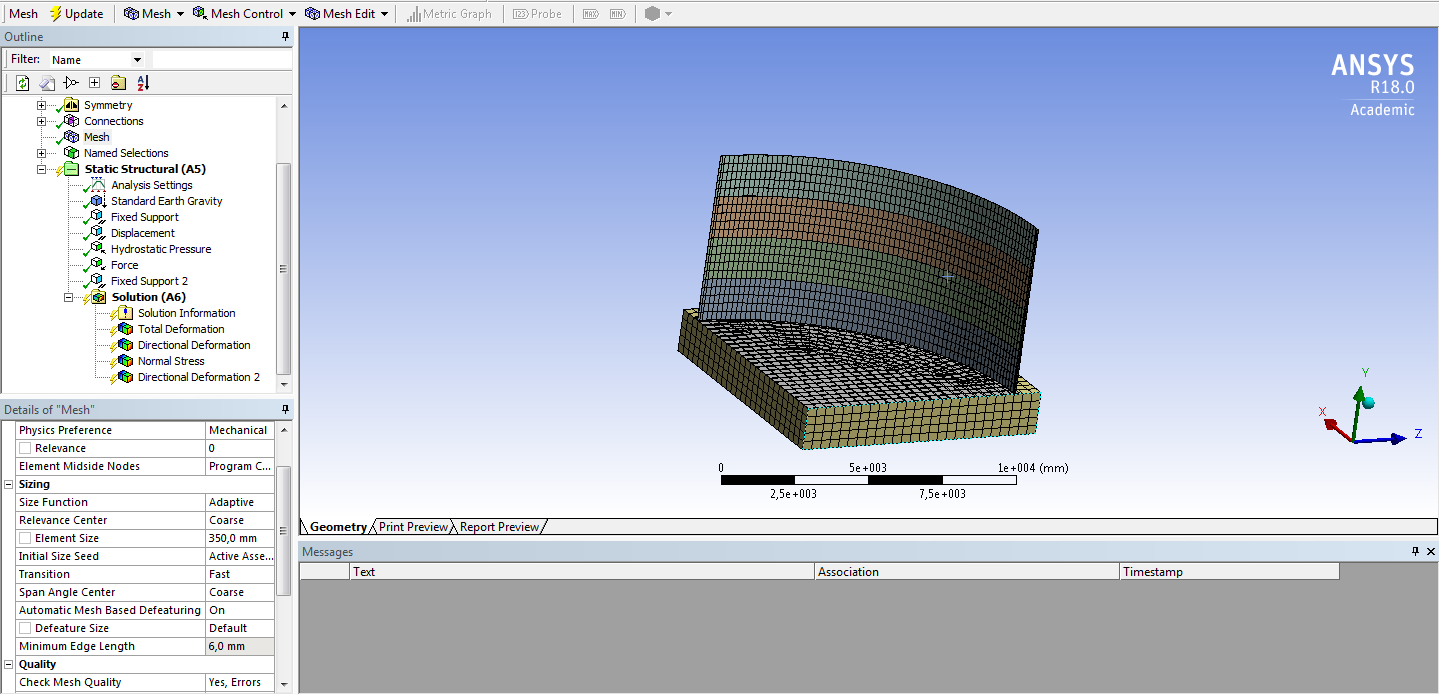 Рисунок 3.16 Изменение сетки конечных элементов Теперь можно производить необходимые расчеты. Так как все необходимые нагрузки в модели определены, проверяем только наличие контакта между днищем резервуара и фундаментом и переходим к этапу расчета. Здесь нам необходимо определить радиальные перемещения стенки резервуара, этот расчет уже задан, необходимо лишь обновить его, выполнив команду Solve. Радиальные перемещения по оси X определены на рисунке 3.12. Для построения диаграммы по оси Y необходимо с помощью инструмента Probe снять в ряде точек поперечного сечения стенки снять значения деформаций в этих точках. На рисунке 3.17 показан ряд значений радиальных деформаций вдоль вертикальной оси. 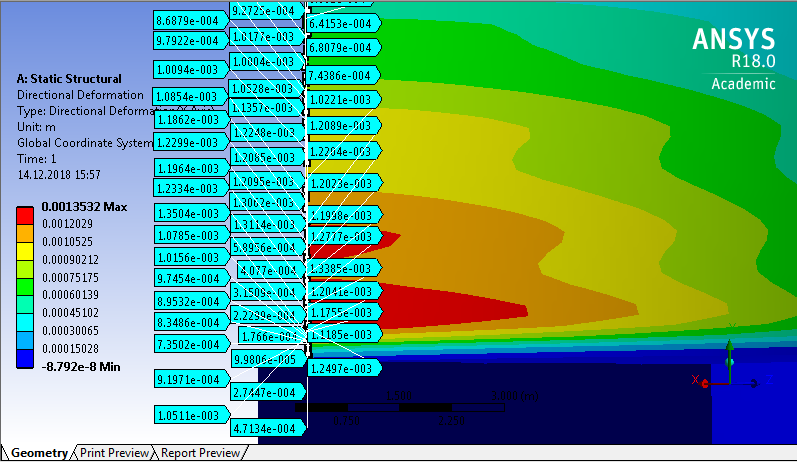 Рисунок 3.17 Радиальные деформации стенки резервуара Значения радиальных перемещений стенки резервуара, снятые с модели, отображаются в отдельной таблице (см. рис. 3.18). Данные из этой таблицы можно скопировать и вставить в рабочую область программы Microsoft Excel. На рисунке 3.19 показана диаграмма радиальных перемещений стенки вертикального стального резервуара под действием приложенной нагрузки. 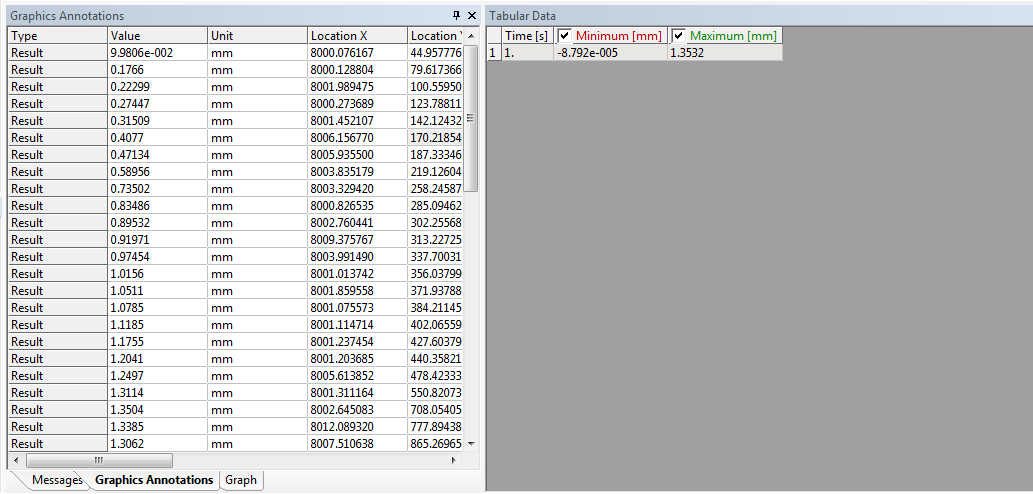 Рисунок 3.18 Таблица значений снятых с модели проб 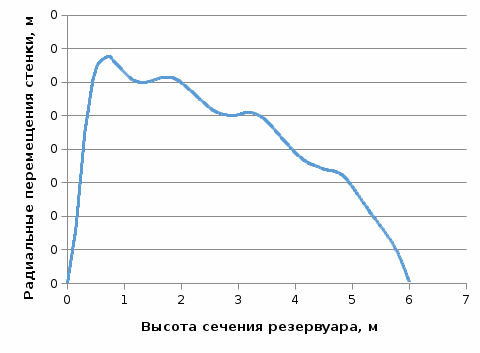 Рисунок 3.19 Диаграмма радиальных перемещений стенки резервуара 3.4 Моделирование сферической крыши резервуараСоздаем новый эскиз в плоскости XYPlane, в котором чертим основу для геометрической модели сферической крыши. Крыша состоит из основания и опорных балок, которые идут от опорного кольца. Количество опорных балок выбирается по размеру окружности резервуара, принимаем для данной модели N = 16. Основание крыши строится вращением прямоугольного сечения кольца при помощи команды Rotate. Опорное центральное кольцо в верхней части крыши строится командой Rotate как Surface body. Для построения одной сферической балки сначала определяем в перпендикулярной сечению балки плоскости траекторию протягивания и используем команду Sweep. Затем рассекаем балку поверхностью центрального кольца командой Slice и удаляем часть внутри кольца. Создаем 15 копий полученной балки командой Pattern вдоль окружности. На рисунках 3.20 – 3.22 показаны этапы разработки геометрической модели крыши.  Рисунок 3.20 Эскиз сечений сферической крыши 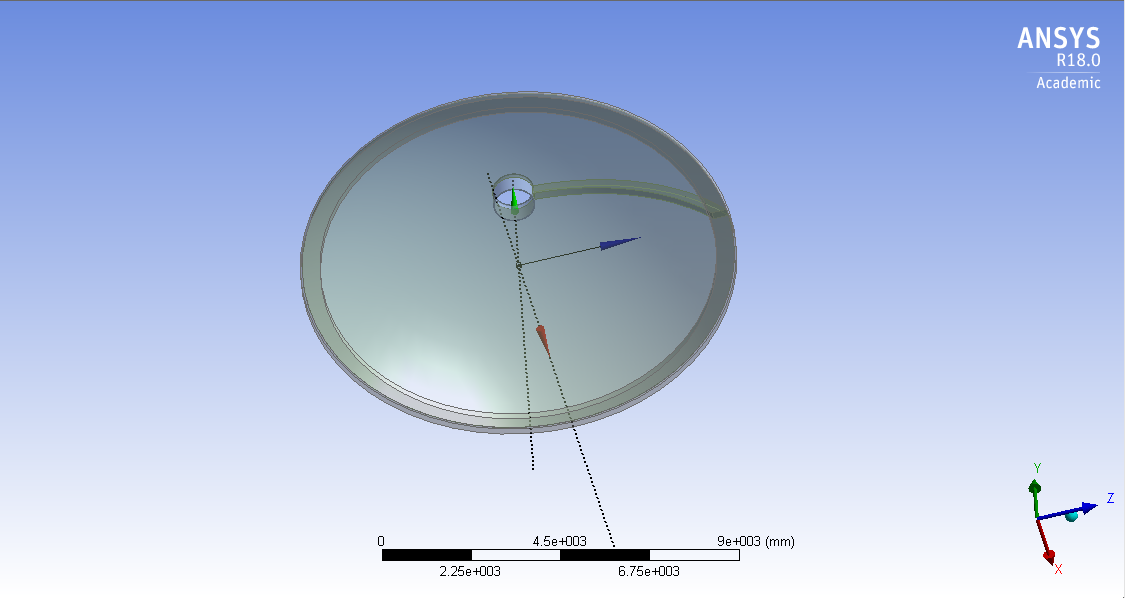 Рисунок 3.21 Геометрическая модель основных элементов крыши 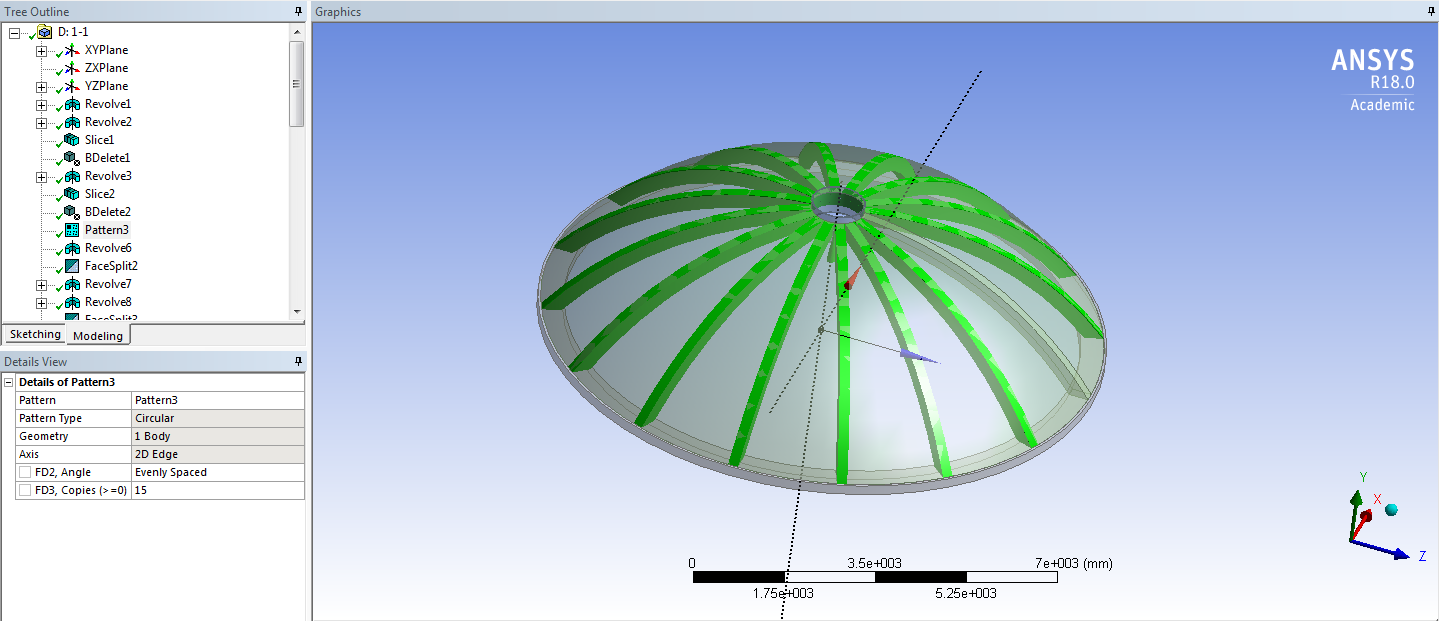 Рисунок 3.22 Результат копирования балок Приложен с помощью команды Pressure сверху на крышу давление о тснеговой нагрузки и собственного веса. Принимаем его равным 0,1 МПа. Результат нагрузки показан на рисунке 3.23.  Рисунок 3.23 Приложение давления к сферической крыше Далее переходим к расчету крыши. Определяем для нее полные деформации (см. рис. 3.24) и эквивалентные напряжения по Мизесу (см. рис. 3.25). Таким образом, мы наиболее полно показали напряженно-деформированное состояние крыши резервуара. 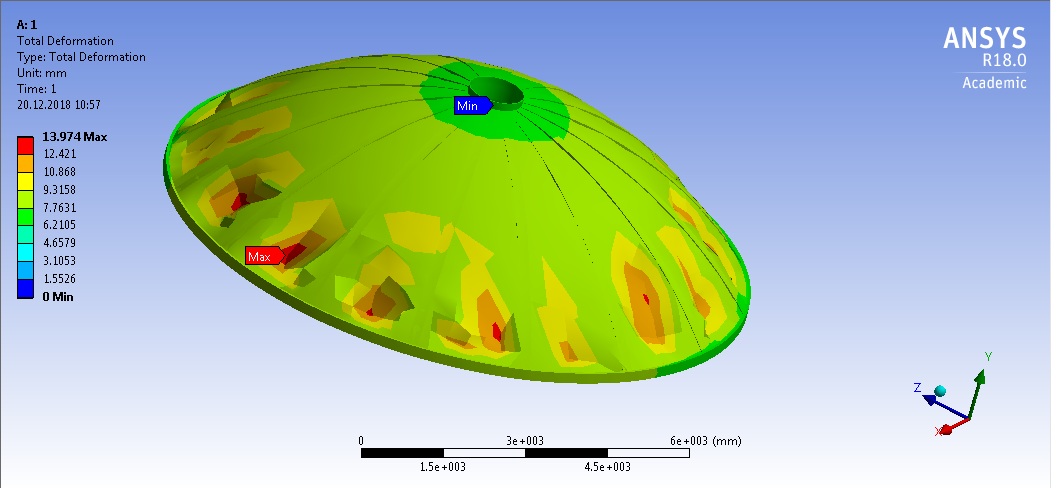 Рисунок 3.24 Полные деформации сферической крыши 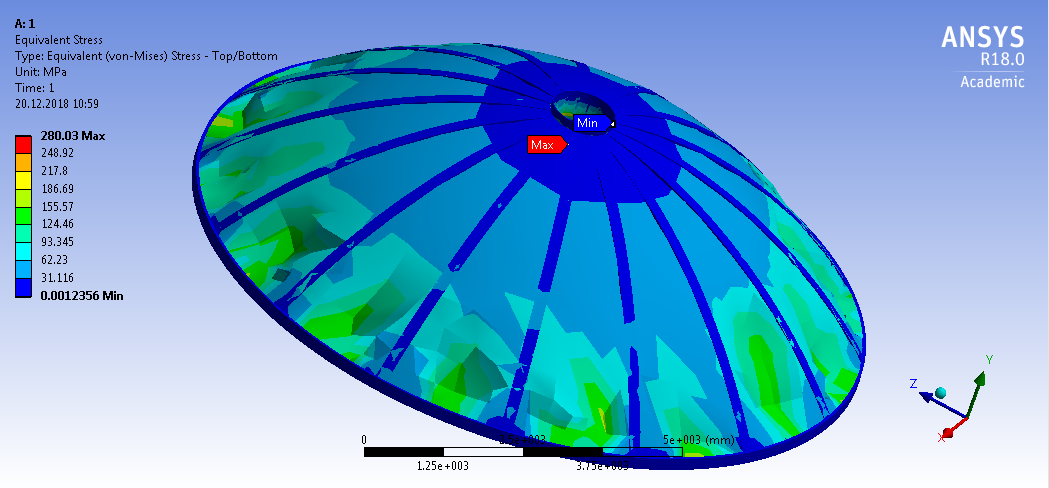 Рисунок 3.25 Эквивалентные напряжения в сферической крыше 3.5 Моделирование резервуара с Z-образным компенсаторомПостроим теперь полную модель резервуара на грунтовой подушке со сферической крышей и Z-образным компенсатором. Сначала на плоскости XYPlane создаем новый эскиз и чертим окружность заданного диаметра трубы. Затем в плоскости YZPlane от центра этой окружности (центр координат) чертим траекторию Z-образного компенсатора, задавая ей необходимые размеры. На рисунке 3.26 показана линия траектории модулируемого Z-образного компенсатора. 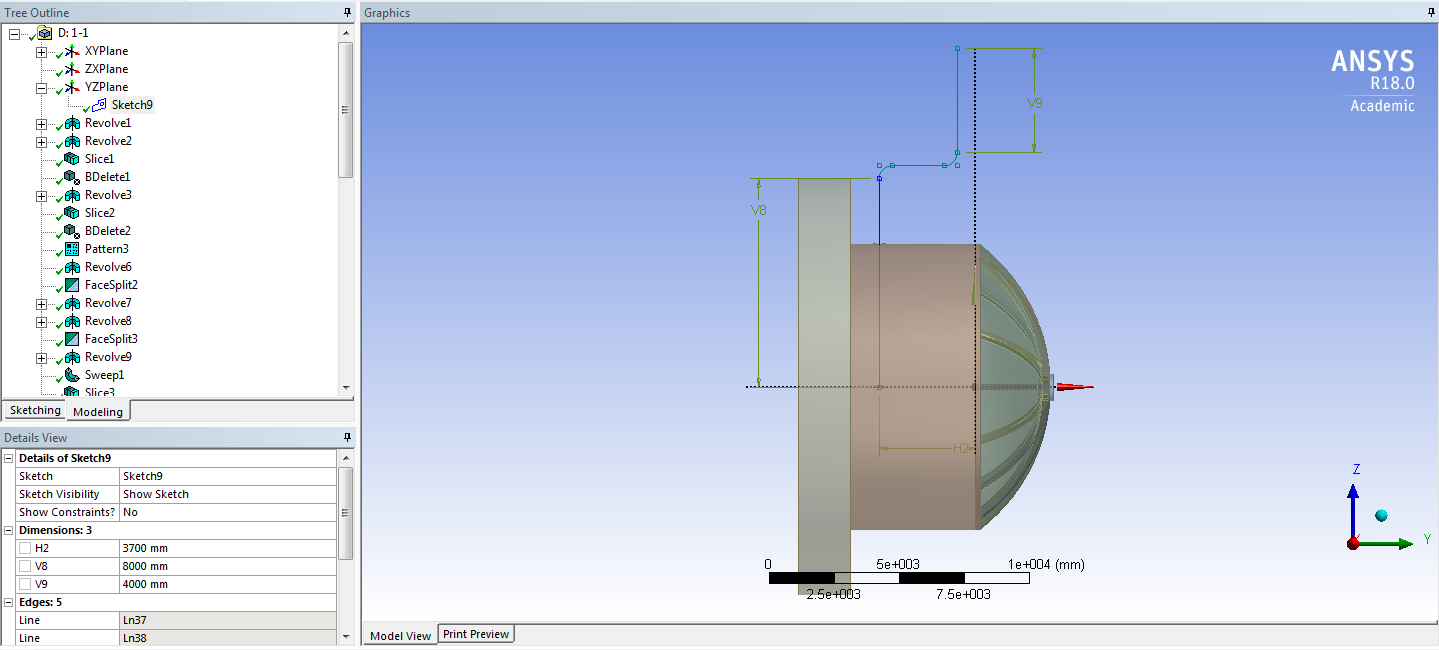 Рисунок 3.26 Эскиз траектории Z-образного компенсатора С помощью команды Sweep протягиваем сечение трубы вдоль построенной траектории, в строке As Thin/Surface? Выбираем Yes и строим как Surface body. Далее командой Slice разрезаем полученную трубу поверхностью стенки резервуара и удаляем часть трубы с внутренне стороны стенки с помощью команды Body Delete. На рисунке 3.27 показана полученная в результате геометрическая модель компенсатора.  Рисунок 3.27 Геометрическая модель резервуара с Z-образным компенсатором Далее строим сетку конечных элементов выполненной модели. Так как количество и геометрические размеры конструктивных частей резервуара достаточно большие, необходимо сначала укрупнить сетку, задавая в соответствующей строке минимальную величину конечного элемента. На рисунке 3.28 показана сетка конечных элементов модели, подобранная таким образом.  Рисунок 3.28 Окончательный вид сетки конечных элементов модели Задаем граничные условия. Нижнее основание грунтовой подушки резервуара должно быть жестко заделано, поэтому ограничиваем там все перемещения с помощью команды Fixed Support (см. рис. 3.29). Крайнее сечение компенсатора не должно перемещаться вдоль оси трубы, поэтому ограничиваем с помощью команды Displacement перемещения только вдоль оси Z (см. рис. 3.30).  Рисунок 3.29 Ограничение перемещений подошвы фундамента резервуара 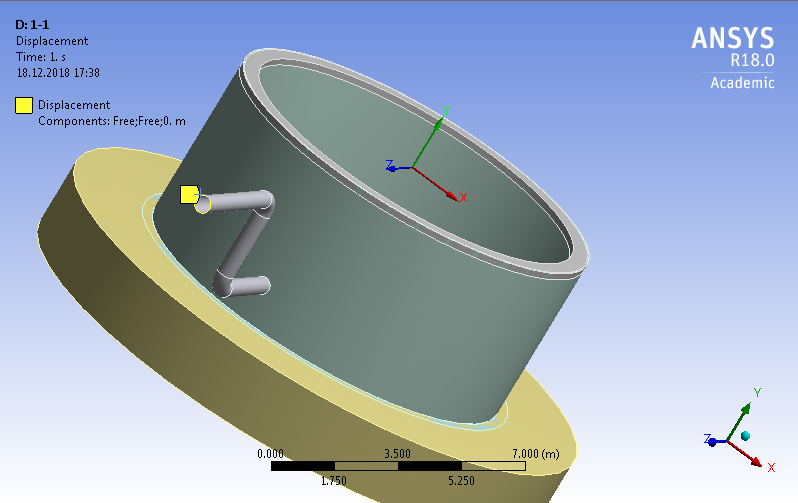 Рисунок 3.30 Ограничение осевых перемещений компенсатора Нагрузку на крышу оставляем в таком виде, в каком она представлена на рисунке 3.24. Внутреннюю полость резервуара нагружаем гидростатическим давлением жидкости, задавая в области параметров команды Hydrostatic Pressure значения плотности жидкости и высоты наполнения резервуара, а также внутреннюю поверхность стенки и днища резервуара, к которым будет приложена нагрузка. На рисунке 3.31 показано нагружение резервуара гидростатическим давлением. 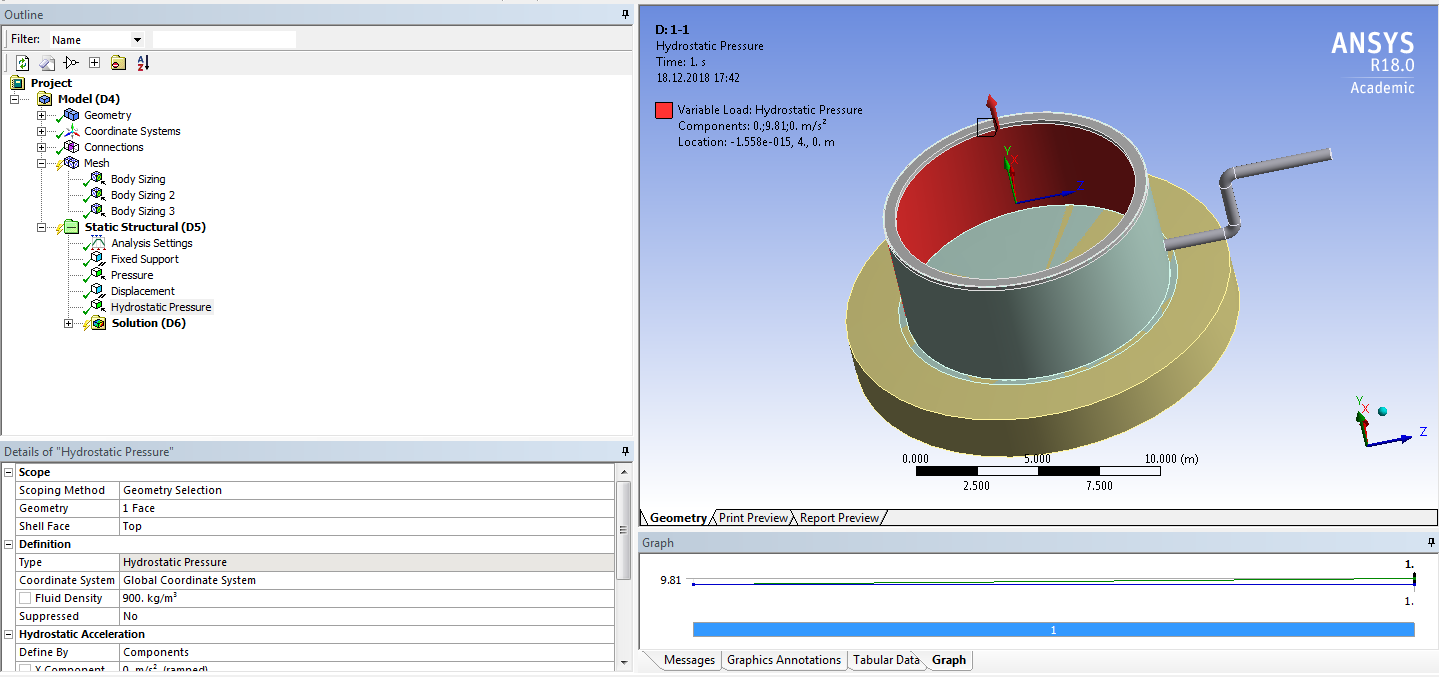 Рисунок 3.31 Нагружение внутренней полости резервуара гидростатическим давлением Определив все нагрузки и ограничив перемещения в крайних точках конструкции, переходим к расчету напряжений (см. рис. 3.32) и деформаций (см. рис. 3.33).  Рисунок 3.32 Эквивалентные напряжения в теле конструкции  Рисунок 3.33 Полная картина линейных перемещений конструкции |
