статистика. Тема 4. 4. 1 студент должен решить задачу, номер которой соответствует
 Скачать 38.71 Kb. Скачать 38.71 Kb.
|
|
Тема 4. СТЕПЕННЫЕ И ПОЗИЦИОННЫЕ Средние величины 4.1. СТЕПЕННЫЕ СРЕДНИЕ ВИЛИЧИНЫ Содержание задания и требования к нему По теме 4.1 студент должен решить задачу, номер которой соответствует варианту. Задача 10. Определить среднюю заработную плату.
Решение: Определим среднюю заработную плату по формуле средней гармонической взвешенной 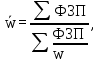 где ФЗП - фонд зарплаты по группе; w – зарплата рабочего в группе. 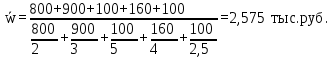 Средняя заработная плата составила 2575 руб. 4.2. ПОЗИЦИОННЫЕ СРЕДНИЕ: МОДА И МЕДИАНА По теме 4.2 студент должен решить задачу, номер которой соответствует варианту. Задача 10. Имеются следующие данные о распределении заводов по расстоянию от железнодорожной станции. Определите моду и медиану.
Решение: 1) Для интервальных вариационных рядов мода определяется по формуле: 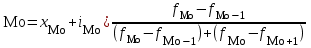 , ,где 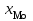 – нижняя граница модального интервала; – нижняя граница модального интервала;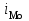 – величина модального интервала; – величина модального интервала;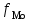 – частота модального интервала; – частота модального интервала;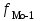 – частота интервала, предшествующего модальному; – частота интервала, предшествующего модальному;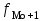 – частота интервала, следующего за модальным. – частота интервала, следующего за модальным.Модальный интервал определяется по наибольшей частоте. Модальный интервал 3-6 км. 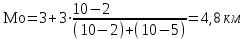 Наиболее часто расстояние от железнодорожной станции составляет 4,8 км.. 2) Медиана интервального ряда определяется по формуле: 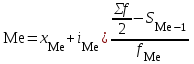 , ,где 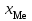 – нижняя граница медианного интервала; – нижняя граница медианного интервала;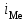 – величина медианного интервала; – величина медианного интервала;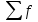 – сумма частот ряда; – сумма частот ряда;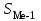 – сумма накопленных частот интервала, предшествующего медианному; – сумма накопленных частот интервала, предшествующего медианному;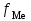 – частота медианного интервала. – частота медианного интервала.Медианным интервалом является интервал 3-6 км, так как именно в этом интервале накопленная частота f= 12 (2+10) впервые превышает величину, равную половине численности единиц совокупности ( 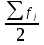 = =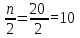 ). ).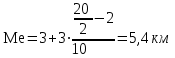 Расстояние от железнодорожной станции одной половины заводов составляет более 5,4 км, а другой половины – менее 5,4 км. |
