4 определение основных характеристик привода 1 Построение и анализ механических характеристик двигателя
 Скачать 128.31 Kb. Скачать 128.31 Kb.
|
4 ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ПРИВОДА4.1 Построение и анализ механических характеристик двигателяДПТ независимого(параллельного) возбуждения имеет линейные механические характеристики и рассчитывается по формуле[]: 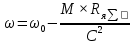 , ,где М – момент, развиваемый двигателем; 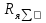 – суммарное сопротивление якорной цепи, включающее внешнее и внутреннее сопротивление якоря двигателя. – суммарное сопротивление якорной цепи, включающее внешнее и внутреннее сопротивление якоря двигателя.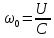 , ,где U – приложенное к якорю напряжение; С – электромеханическая конструктивная постоянная; Падение скорости, определяющее крутизну механической характеристики []: 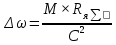 . .Механическая характеристика электропривода ω(М) строится по двум точкам []: 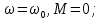 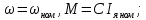 Коэффициент С определяется по формуле []: 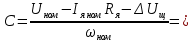 0,4, 0,4,где 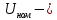 номинальное напряжение, приложенное к якорю, В; номинальное напряжение, приложенное к якорю, В;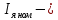 номинальный ток якоря, А; номинальный ток якоря, А;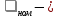 номинальная частота вращения двигателя; номинальная частота вращения двигателя;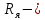 сопротивление обмотки якоря, Ом; сопротивление обмотки якоря, Ом;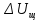 =2 ÷2,7 В – падение напряжения на щеточном контакте. =2 ÷2,7 В – падение напряжения на щеточном контакте.Зная постоянную машины определим скорость идеального холостого хода естественной характеристики: 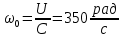 Естественная механическая характеристика ДПТ изображена на рисунке 4.1. 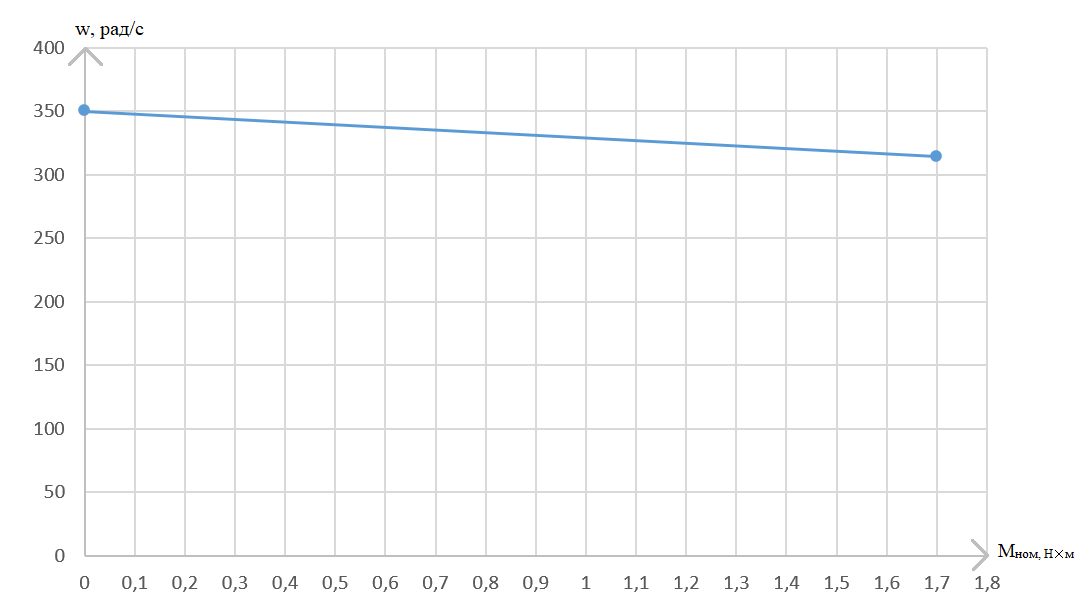 Рисунок 4.1 – Естественная механическая характеристика ДПУ Жесткость механической характеристики определяется как []: β = 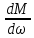 = =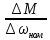 = =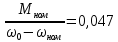 Н×м×с Н×м×с4.2 Расчет скорости для точной остановки и анализ результатовУгловое перемещение вала двигателя т, соответствующее расстоянию Sт, в общем случае складывается из составляющих 1, 2, 3, где 1 – путь, проходимый приводом за абсолютное время срабатывания аппаратуры и равный: 1=нач×Δtсобств где нач – угловая скорость электропривода; Δtсобств – время срабатывания электрических аппаратов; 2 – путь, проходимый за время работы электродвигателя на тормозной характеристике; 3 – путь, проходимый за время действия механического тормоза, эта составляющая обычно мала по сравнению с 1 и 2, поэтому в большинстве случаев её можно не рассчитывать. Для упрощения расчета составляющей 2 можно принимать, что за время торможения скорость электропривода снижается линейно от нач до нуля. Тогда среднее значение скорости при торможении равно нач/2 []. Время торможения Δtт находится из уравнения движения, и при Мд+Мс=Мдин=const, равно: 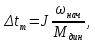 а путь 2=J 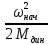 . .Таким образом φт=ωнач×∆tсобств+J 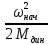 В связи с возможным разбросом действительных значений ωнач, ∆tсобсств, Мдин, J от их среднерасчетных значений путь φт может колебаться от некоторого минимального значения φт min до некоторого максимального φт max. Точность остановки электропривода в этом случае оценивают величиной []: ∆φт= 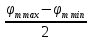 , ,то есть, расчетную точку останова располагают в середине зоны точности. Если действительные значения величин, составляющих ∆φт, представить через средние значения и отклонения от этих средних, то есть []: ωнач=ωср 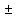 ∆ω, ∆ω,∆tсобств = ∆ 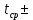 ∆t, ∆t, Мдин = 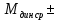 ∆Мдин, ∆Мдин, Jмех=Jср 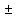 ∆J, ∆J, и учитывая, что ∆φт 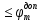 , ,где 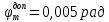 (по условиям курсового проекта), то можно найти скорость двигателя ср из следующей формулы []: (по условиям курсового проекта), то можно найти скорость двигателя ср из следующей формулы []:∆φт=ωср ∆tср 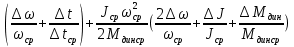 Для расчета зададимся следующими параметрами []: 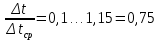 ; Δtcр = 0,2 … 0,3=0,25; ; Δtcр = 0,2 … 0,3=0,25; 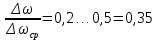 . .Вычисления: Максимальный момент инерции равен: 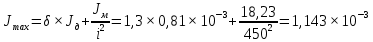 (кг×м2); (кг×м2);Минимальный момент инерции: 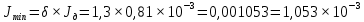 (кг×м2); (кг×м2);Перепад моментов инерции: 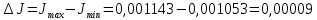 (кг×м2). (кг×м2).Среднее значение момента инерции: 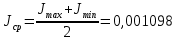 (кг×м2). (кг×м2).Аналогично для динамического момента: 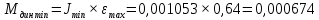 (H×м); (H×м);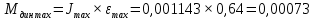 (H×м); (H×м);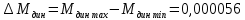 (H×м); (H×м);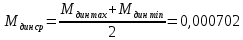 (H×м). (H×м).Подставляя эти значения в уравнение (), получим: 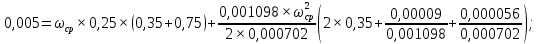 Решая данное уравнение, получим скорость механизма 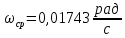 . .Диапазон регулирования скорости в схеме привода определяется по формуле: 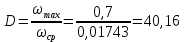 4.3 Расчет и анализ переходных процессовХарактер переходного процесса зависит от инерционности. Если Тм>Тэ, то можно рассматривать только механический переходной процесс, обусловленный механической инерцией. Если Тм = Тэ, то следует учитывать обе постоянные времени и рассчитывать электромеханический переходной процесс. Результатом расчета переходных процессов является зависимости угловой скорости и момента от времени, то есть 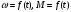 []. [].Электромагнитная постоянная времени цепи якоря двигателя: Тэ= 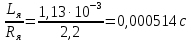 Вычислим электромеханическую постоянную времени для двигателя постоянного тока независимого возбуждения []: 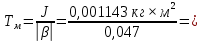 0,0243 с; 0,0243 с;где J – суммарный, приведенный к валу двигателя момент инерции. В данном случае Тм в значительно больше Тэ, поэтому можно принять Тэ = 0 и вместо электромеханического можно рассматривать только механический переходной процесс. При расчете переходных процессов определяются зависимости угловой скорости и момента от времени, т.е. ω(t) и M(t). Угловая скорость задается по закону: ω0(t)=ω0нач+ε0t, где ω0нач – заданная скорость при t=0; ε0 – заданное значение углового ускорения(замедления). В этом случае угловая скорость двигателя рассчитывается следующим образом [м]: ω =ε0t+( ω0нач - ∆ωст - ε0Тм) (1 - 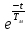 ) + ωнач ) + ωнач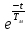 , ,где ∆ωст – статическое падение скорости двигателя; ωнач – начальная скорость двигателя. Находим статическое падение угловой скорости двигателя []: ∆ωст = 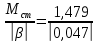 = 31,468 рад/с = 31,468 рад/сЭлектромагнитный момент двигателя определяется выражением: М = Мст + Jε0 + (Мнач - Мст - Jε0) 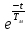 , ,где Мнач – начальное значение электромагнитного момента двигателя. Моменты, приложенные к механической системе со стороны двигателя, называются движущими, со стороны нагрузки – моментами сопротивления. Моменты сопротивления разделяются на активные и реактивные. Пуск при активном статическом моменте: На интервале времени 0 < t < tп, где tп – заданное время пуска, имеем: ω = ε0t - (∆ωст + ε0Тм) (1- 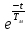 ), ),М = Мст + Jε0 (1- 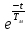 ) - Мст ) - Мст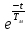 . .На интервале tп < t < tп + 3Тм: ω = ω0кон - ∆ωст - ε0Тм 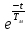 , ,где ω0кон – конечное значение заданной угловой скорости; М = Мст + Jε0 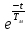 . .Торможение при активном статическом моменте: На интервале времени 0 < t < tт, где tт –время торможения, имеем: ω = ω0нач - ∆ωст - ε0t + ε0Тм (1- 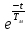 ), ),М = Мст - Jε0 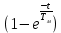 . .На интервале tт < t < tт + 3Tм: ω = -∆ωст + ε0Тм 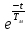 , ,М = Мст - Jε0 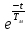 . .Абсолютное значение заданного углового ускорения как для пуска (t0 = tп, ω0кон = ωуст), так и для торможения (t0 = tт, ω0нач = ωуст) двигателя выразим следующим образом: ε0 = 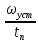 ; ;ε0 = 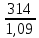 = 288 рад/с2. = 288 рад/с2.Подставив все известные величины в формулы () – (), получим следующие переходные характеристики: а) для пуска: ω(t)= 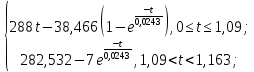 M(t)= 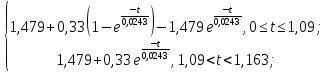 б) для торможения: ω(t)= 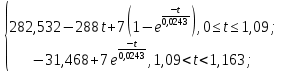 M(t)= 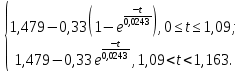 На рисунках 4.2-4.5 приведены графики зависимостей ω=f(t) и M=f(t) для режимов пуска и торможения. 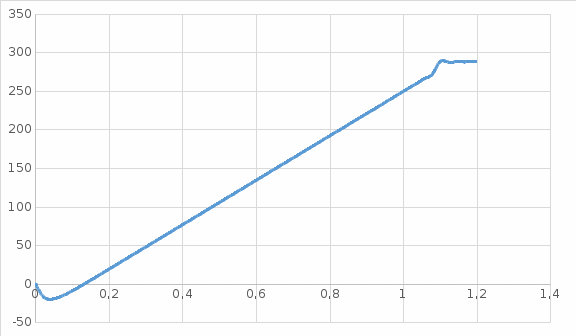 Рисунок 4.2 – Переходной процесс по угловой скорости при пуске 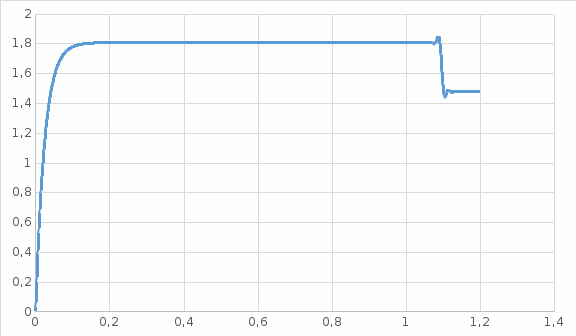 Рисунок 4.3 – Переходной процесс по моменту при пуске 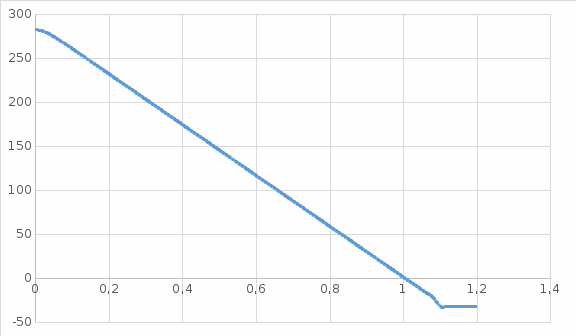 Рисунок 4.4 – Переходной процесс по угловой скорости при торможении 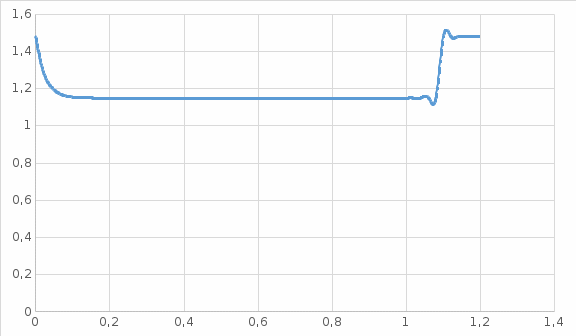 Рисунок 4.5 – Переходной процесс по моменту при торможении Анализ графиков переходных процессов выбранного двигателя показывает, что. |
