Контр_ДУ_7. Решение Данное дифференциальное уравнение однородное дифференциальное уравнение первого порядка. Для решения сделаем замену
 Скачать 45.51 Kb. Скачать 45.51 Kb.
|
|
Контрольная работа №1 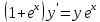 Решение: Данное дифференциальное уравнение является уравнением с разделяющимися переменными, разделим переменные и проинтегрируем обе части, получим: 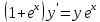 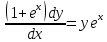 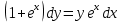 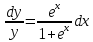 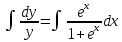  Ответ:  №2 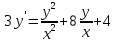 Решение: Данное дифференциальное уравнение – однородное дифференциальное уравнение первого порядка. Для решения сделаем замену: 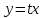 Тогда:  Подставляем в уравнение: 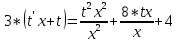  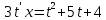 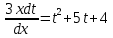 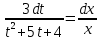 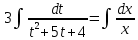 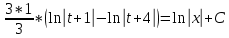 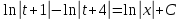 Сделаем обратную замену и получим общий интеграл исходного дифференциального уравнения: 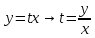 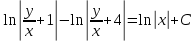 Ответ: 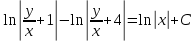 №3 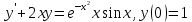 Решение: Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Для решения сделаем замену: 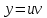 Тогда: 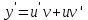 Подставляем в уравнение: 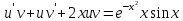 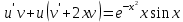 Получаем систему уравнений: 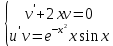 Решим первое уравнение системы: 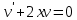 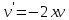 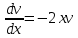 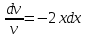 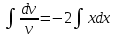 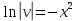 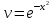 Подставим полученное решение во второе уравнение системы: 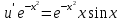 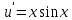 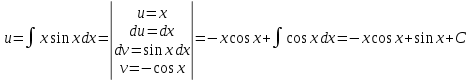 Сделаем обратную замену и получим общее решение исходного дифференциального уравнения:  Теперь найдём решение задачи Коши, для этого воспользуемся начальным условием: 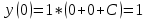 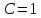 Тогда решение задачи Коши выглядит так: 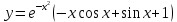 Ответ: 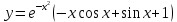 №4  Решение: Данное дифференциальное уравнение является уравнением Бернулли. Разделим на  обе части: обе части: 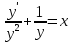 Сделаем замену:  Находим производную: 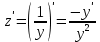 Подставляем в уравнение: 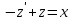 Домножим обе части на (-1): 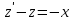 Получили линейное неоднородное дифференциальное уравнение первого порядка. Для решения сделаем замену: 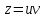 Тогда:  Подставляем в уравнение: 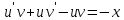 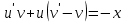 Получаем систему уравнений: 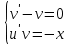 Решим первое уравнение системы: 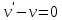 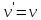 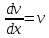  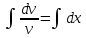   Подставим полученное решение во второе уравнение системы: 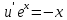 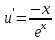 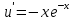 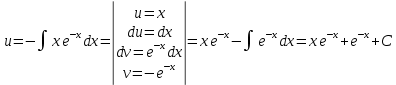 Сделаем обратную замену: 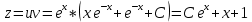 Сделаем ещё одну обратную замену и получим общее решение исходного дифференциального уравнения: 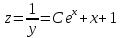 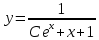 Чтобы найти решение задачи Коши, воспользуемся начальным условием: 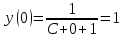 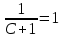 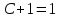 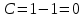 Тогда решение задачи Коши выглядит так: 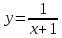 Ответ: 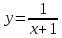 №5 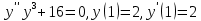 Решение: Данное дифференциальное уравнение в явном виде не содержит переменную x, поэтому для решения сделаем замену: 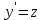 Тогда: 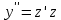 Подставляем в уравнение: 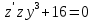 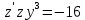 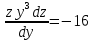 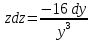 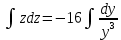 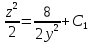 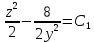 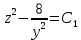 Сделаем обратную замену: 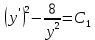 Воспользуемся начальным условием: 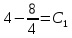 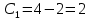 Тогда: 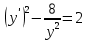 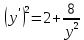 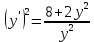 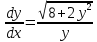 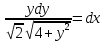 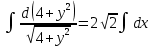 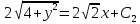 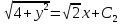 Воспользуемся начальным условием: 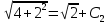 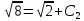 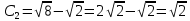 Тогда: 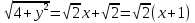 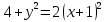 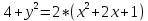 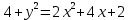 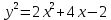 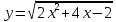 Ответ: 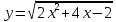 №6 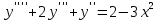 Решение: Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением четвёртого порядка. Сначала найдём общее решение соответствующего однородного уравнения, для этого составим характеристическое уравнение и найдём его корни: 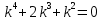    Так как получены действительные корни, один из которых равен нулю, общее решение однородного уравнения выглядит так: 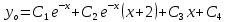 Частное решение неоднородного уравнения ищем в виде: 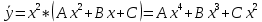 Найдём первую и вторую, третью и четвёртую производные от данного выражения: 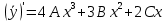 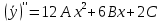 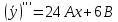 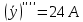 Подставляем в уравнение: 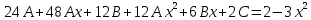 Приравнивая коэффициенты перед соответствующими степенями, получаем систему уравнений: 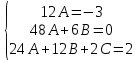 Решив данную систему, получим, что: 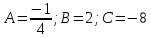 Тогда частное решение неоднородного уравнения выглядит так: 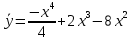 Общее решение неоднородного уравнения выглядит так: 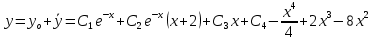 Ответ: 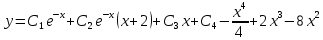 №7 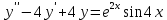 Решение: Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением второго порядка. Сначала найдём общее решение соответствующего однородного уравнения, для этого составим характеристическое уравнение и найдём его корни: 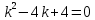 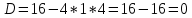 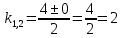 Так как получены одинаковые действительные корни, общее решение однородного уравнения выглядит так: 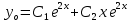 Частное решение неоднородного уравнения ищем в виде: 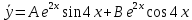 Найдём первую и вторую производные от данного выражения: 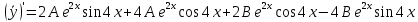 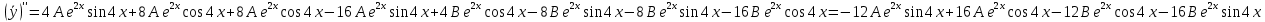 Подставляем в уравнение: 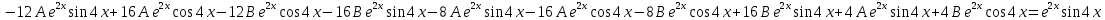 Приводим подобные слагаемые в левой части: 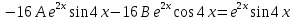 Приравнивая коэффициенты между соответствующими выражениями, получаем систему уравнений: 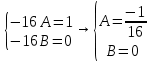 Тогда частное решение неоднородного уравнения выглядит так: 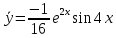 Общее решение неоднородного уравнения выглядит так: 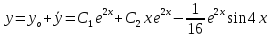 Ответ: 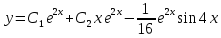 |
