расчет. 5. Исполнительный механизм
 Скачать 416.46 Kb. Скачать 416.46 Kb.
|
|
Исходные данные: Схема привода 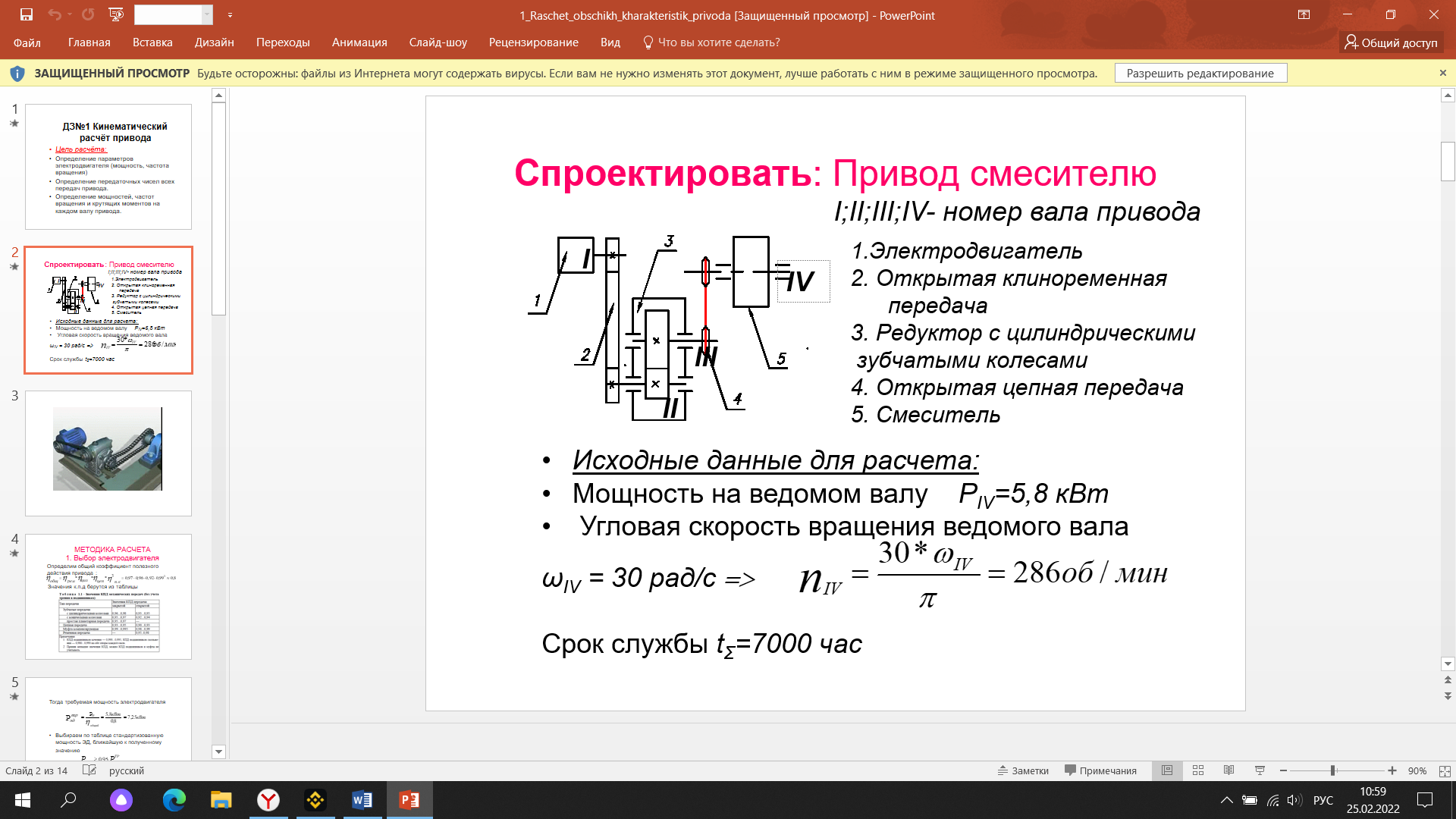  5. Исполнительный механизм T4 = (14) кН*м; n4 = (22) об/мин. 1) Подбор электродвигателя ηобщ = ηрем * ηцил * ηцеп * η³п.к.= 0,965* 0,97*0,915*0,985³ = 0,819 Требуемая мощность электродвигателя: 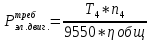 = = 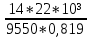 = 39,38кВт => = 39,38кВт => 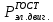 = 45кВт = 45кВтОсновные параметры электродвигателя: Марка: 4А250M8Y3 Частота вращения: nсинх = 750об\мин nасинх = nсинх*(1- 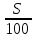 )= 750*(1- )= 750*(1-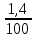 )= 739,5 об/мин )= 739,5 об/мин22*[1,5…3,5]*[3,15…5]*[1,5…3] = 155,925…1155 об/мин 2)Определение передаточных чисел механических передач: Uобщ = 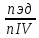 = = 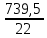 = 33,614; = 33,614; 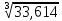 = 3,227 = 3,227Примем: Uзуб = 4,5; => Uрем * Uцеп = 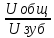 = = 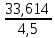 = 7,469 = 7,469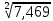 = 2,733 => Uрем =3 = 2,733 => Uрем =3 Uцеп = 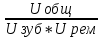 = = 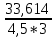 = 2,4899 ∈[1,5…3] = 2,4899 ∈[1,5…3] Принимаем: Uзуб = 4,5; Uрем =3; (3), Uцеп = 2,4899. 3) Определение силовых и кинематических характеристик валов привода: n1 = nэд = 739,5 об/мин; n2 = 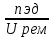 = =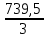 = 246,5 об/мин; = 246,5 об/мин;n3 = 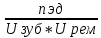 = =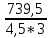 = 54,778 об/мин; = 54,778 об/мин;n4 = 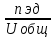 = =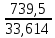 = 22 об/мин; = 22 об/мин;Р1 = Рэд = 45 кВт; Р2 = Рэд* ηрем * ηп.к.= 45*10³*0,96*0,985= 42,552 кВт; Р3 = Р2* ηзуб * ηп.к.= 42,552*0,97*0,985= 40,656 кВт; Р4 = Р3* ηцеп * ηп.к.= 40,656*0,91*0,985= 36,442 кВт; Т1 = 9550 * 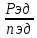 = 9550 * = 9550 *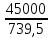 = 581,135 Н*м; = 581,135 Н*м;Т2 = 9550 * 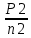 = 9550 * = 9550 *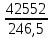 = 1,649 кН*м; = 1,649 кН*м;Т3 = 9550 * 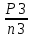 = 9550 * = 9550 *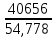 = 7,088 кН*м; = 7,088 кН*м;Т4 = 9550 * 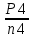 = 9550 * = 9550 *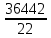 = 15,819 кН*м; = 15,819 кН*м;ΔТ = 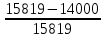 *100% = 11,5% *100% = 11,5% Расчет зубчатых передач редуктора Крутящий момент на шестерне Т1=ТII = 1,649 кН*м; Крутящий момент на колесе Т2=ТIII = 7,088 кН*м; Частота вращения шестерни n1=nII = 246,5 об/мин; Частота вращения колеса n2=nIII = 54,778 об/мин; Передаточное число U=Uцил = 4,5 Срок службы tΣ = 18000 ч. 1. Выбор материалов По рекомендациям для T2 > 2000 H*м принимаем: Шестерня: марка стали -12ХН3А , вид термообр. - Ц, твёрдость = 380 HB; σт = 800МПа; Колесо: марка стали – 20ХНМ, вид термообраб. - Ц, твердость = 320 HB; σт = 800 МПа 2. Определение допускаемых напряжений : а) при расчете на контактную прочность 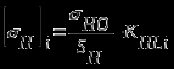 где σH0 - предел контактной выносливости при базовом числе циклов нагружения (находим по таблице) Для шестерни HRC = 63; σH0 = 23HRC = 23*63 = 1449 МПа; Для колеса HRC = 55; σH0 = 23HRC = 23*55 = 1265 МПа; SH= 1,2 - коэффициент запаса для шестерни и колеса (т.к. вид термообработки – Ц) Базовое число циклов: NHO ≈30(HB)2,4 Для шестерни: NHO1 = 30*(380)2,4 = 46623179 Для колеса: NHO1 = 30*(320)2,4 = 30866060 Для шестерни: NΣi = 60*18000*246,5 = 266 220 000 Для колеса: NΣi = 60*18000*54,778 = 59 160 240 KHL-коэффициент долговечности, зависит от длительности работы передачи 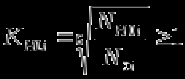 Если N∑i> NHOi , то KHLi=1 Для шестерни: KHL1=1 Для колеса: KHL2=1 Получаем: Для шестерни: [ 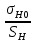 KHL1 = KHL1 = 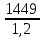 МПа; МПа; Для колеса: [ 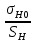 KHL2 = KHL2 =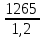 МПа; МПа;Окончательно, расчетные допускаемые контактные напряжения для косозубых колес принимаем [𝜎H]= [𝜎𝐻]2 = 1054,167 МПа б) при расчете на прочность при изгибе 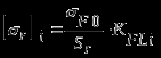 (𝑖=1,2) (𝑖=1,2) где σFo – предел выносливости Для шестерни: σFo= 840 МПа Для колеса: σFo=760 МПа SF=1,75 – коэффициент запаса KFL – коэффициент долговечности 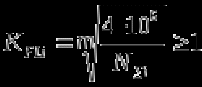 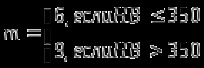 Если N∑i > 4∙106 , то KFLi=1 Так как для шестерни и колеса N∑i > 4∙106 , то KFL1=1 и KFL2=1 Получаем: [σF]1 = 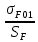 * KFL1 = * KFL1 = 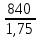 * 1 = 480 МПа * 1 = 480 МПа[σF]2 = 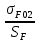 * KFL2 = * KFL2 = 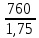 * 1 = 434,286 Мпа. * 1 = 434,286 Мпа.Окончательно принимаем [σF] = [σF]2 = 434,286 Мпа. в) при кратковременной перегрузке Допускаемые контактные напряжения при перегрузке [𝜎𝐻]𝑚𝑎𝑥=44* HRC Для шестерни: [𝜎𝐻]𝑚𝑎𝑥1= 44*63 = 2772 МПа Для колеса: [𝜎𝐻]𝑚𝑎𝑥2=44*55 = 2420 МПа Расчетные максимальные допускаемые контактные напряжения при перегрузке: [𝜎𝐻]𝑚𝑎𝑥 = 2420 МПа Допускаемые напряжения при изгибе 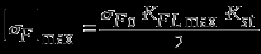 Для шестерни: KFLmax1=2,5, Kst1=1,2 => [σF]max = 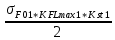 = = 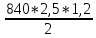 =1260 МПа =1260 МПаДля колеса: KFLmax2=2,5, Kst1=1,2 => [σF]max = 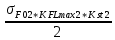 = = 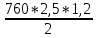 =1140 МПа =1140 МПаПримем [σF] = [σF]2 = 1140 МПа 3. Проектный расчет передачи из условия контактной прочности. 3.1 Определение межосевого расстояния 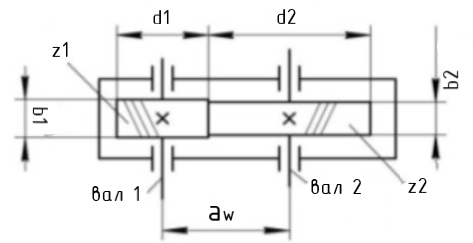 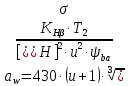 Коэффициент ширины венца по межосевому расстоянию выбираем из стандартного ряда 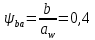 Коэффициент ширины шестерни по диаметру 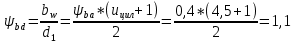 Коэффициент неравномерности распределения нагрузки по ширине венца 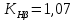 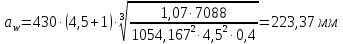 полученное 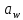 округляем до ближайшего значения из стандартного ряда округляем до ближайшего значения из стандартного ряда 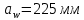 3.2 Определение основных геометрических параметров Основное равенство, связывающее параметры косозубой передачи 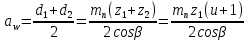 Модуль зацепления m= (0,01-0,02)*aW = 2,25 - 4,5мм Принимаем стандартное значение 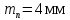 Принимаем предварительный угол наклона линии зубьев: 𝛽 = 15° Число зубьев: 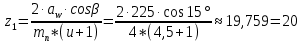 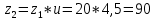 Фактическое передаточное число 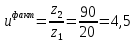 Проверяем отклонение фактического передаточного числа от заданного 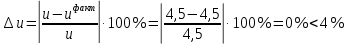 Уточняем угол β 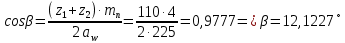 Основные размеры шестерни и колеса Высота головки зуба: ℎ𝑎 = 𝑚𝑛 = 4 мм Высота ножки зуба: ℎ𝑓 = 1,25 ∙ 𝑚𝑛 = 5 мм Высота зуба: ℎ = ℎ𝑎 + ℎ𝑓 = 4 + 5 = 9 мм Диаметры делительных окружностей Для шестерни: 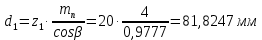 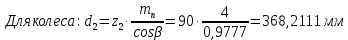 Проверка: 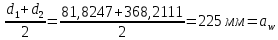 Диаметры окружности вершин da и впадин df зубьев 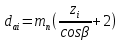 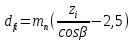 Для шестерни: 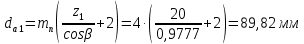 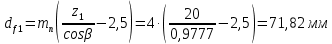 Для колеса: 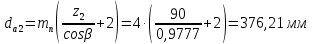 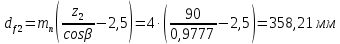 Ширина зубчатого венца колеса: 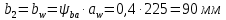 Ширина зубчатого венца шестерни: 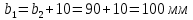 Окружная скорость колеса: 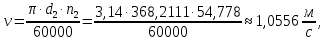 4.Силы в цилиндрическом зацеплении 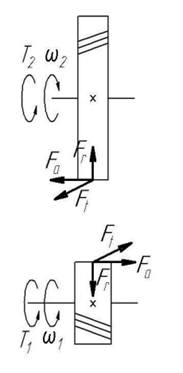 Окружная сила 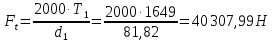 Радиальная сила 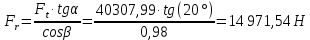 Осевая сила 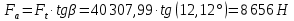 5.Проверочные расчеты передач 5.1Расчет на контактную выносливость поверхности зубьев 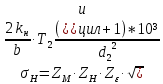 Коэффициент, учитывающий механические свойства материала колес: 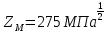 Коэффициент, учитывающий форму сопряженных поверхностей зубьев: 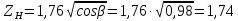 Коэффициент торцового перекрытия для внешнего зацепления: 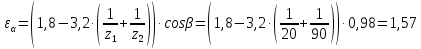 Коэффициент, учитывающий суммарную длину контактных линий: 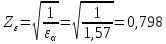 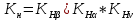 =1,05*1,03*1,01=1,09 =1,05*1,03*1,01=1,09Коэффициент концентрации нагрузки: 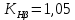 Коэффициент неравномерности распределения нагрузки между зубьями:  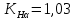 Динамический коэффициент: 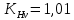 Расчетное контактное напряжение 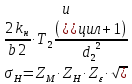 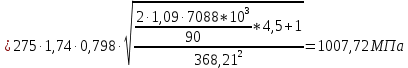 Критерий оптимальности: 0,85[𝜎𝐻] ≤ 𝜎𝐻 ≤ 1,05[𝜎𝐻] 896,042 МПа ≤ 1007,72 МПа ≤1106,875 МПа Передача удовлетворяет условию контактной прочности. 5.2Расчет зубьев на выносливость при изгибе Эквивалентные числа зубьев шестерни и колеса: 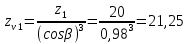 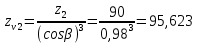 Коэффициенты формы зуба шестерни и колеса 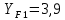 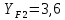 Коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии к основанию зуба и неравномерного распределения нагрузки 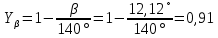 Коэффициент, учитывающий распределение нагрузки между зубьями 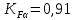 Коэффициент, учитывающий распределение нагрузки по ширине зубчатого венца при изгибе 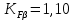 Коэффициент, учитывающий динамическую нагрузку при изгибе 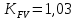 Расчетное напряжение при изгибе для шестерни: 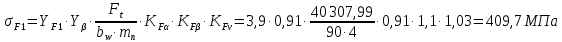 для колеса: 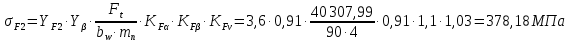 Критерий оптимальности: 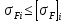 для шестерни: 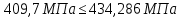 для колеса: 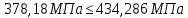 5.3Расчет зубьев на прочность при кратковременной перегрузке Контактная прочность 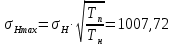 * * 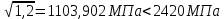 При изгибе 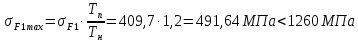 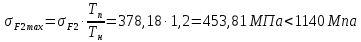 |
