Р5- (Истечение жидкости через отв. и насадки). 5. истечение жидкости через отверстия и насадки 1 Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
 Скачать 0.88 Mb.
|
|
5. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ 5.1 Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре Истечение жидкости через отверстия и насадки характерно тем, что в процессе истечения запас потенциальной энергии, которым обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую энергию свободной струи. Основным вопросом в данном случае является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков. Возьмем большой резервуар с жидкостью (рис. 5.1), который имеет малое отверстие в стенке на достаточно большой глубине Н от свободной поверхности. Через отверстие жидкость вытекает свободной струей.   Рис. 5.1. Истечение жидкости из Рис. 5.2. Тонкая стенка резервуара Малым отверстием называется такое, у которого диаметр  не превышает 0,1 величины напора Н. При этом условии можно считать давление и скорость жидкости во всех точках отверстия одинаковыми.Стенки подразделяются на тонкие и толстые. Тонкой стенкой (рис. 5.2) называют такую, толщина которой не влияет на характер истечения, т.е. отсутствуют путевые потери. Опытами установлено, что толщина тонкой стенки не должна превышать 1,0…1,5 диаметра, т.е.  (1…1,5) .Частицы жидкости (см. рис. 5.2) приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различным плавным траекториям. Вытекающая из отверстия струя не сохраняет свою форму, а постепенно деформируется, т.е. отрывается от стенки у кромки отверстия и несколько сжимается. Цилиндрическую форму струя принимает на расстоянии (0,5…1,0) от плоскости отверстия. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения частиц жидкости в резервуаре, в том числе от радиального направления движения по стенке, к осевому направлению движения в струе.Коэффициентом сжатия называется отношение площади сжатого сечения струи  к площади отверстия  , т.е. . (5.1)Сжатие струи может быть полным и неполным. Полное сжатие – это всестороннее сжатие. Оно имеет место тогда, когда отверстие в достаточной мере удалено от боковых поверхностей стенок сосуда. Если же часть периметра отверстия совпадает с боковой стенкой или днищем сосуда, то сжатие струи будет неполным. Полное сжатие может быть совершенным или несовершенным. Сжатие считается совершенным, если до ограждающих поверхностей будет не менее трех размеров отверстия, и несовершенным, если расстояние до стенок или дна – менее трех размеров отверстия. Найдем скорость истечения и расход жидкости при истечении жидкости через малое отверстие в тонкой стенке (рис. 5.3).  Рис. 5.3. Истечение жидкости через малое отверстие в тонкой стенке Возьмем сосуд с жидкостью. В стенке выполнено малое отверстие на глубине Н от свободной поверхности жидкости. Возьмем два сечения 1–1 и 2–2 по свободной поверхности жидкости и в сжатом сечении струи соответственно. За плоскость сравнения примем горизонтальную плоскость, проходящую через центр тяжести отверстия. Составим уравнение Бернулли для сечений 1–1 и 2–2 в общем виде:  , (5.2)где  – геометрическая высота сечения 1–1,  ;  – давление в сечении 1–1,  ;  – скорость в сечении 1–1, скорость можно считать раной нулю, = 0, так как из уравнения расходов  следует, что  , но так как   , то = 0;  – геометрическая высота сечения 2–2, = 0;  ;  – коэффициент Кориолиса в сечении 1–1, = 1,0;  – коэффициент, учитывающий неравномерность распределения скоростей в сжатом сечении, при равномерном распределении скоростей в струе  ;  – скорость в сжатом сечении струи, ;  – потери напора при движении жидкости через отверстие.Потери напора (удельной энергии) при движении жидкости через отверстие вызываются местными сопротивлениями, т.е. можно определять по формуле Вейсбаха:  , (5.3)где  – коэффициент местного сопротивления отверстия.С учетом вышеизложенного уравнение Бернулли (5.2) запишется следующим образом:  , или  . (5.4)Решим уравнение (5.4) относительно скорости  , получим . (5.5)Обозначим через  выражение:  , которое называется коэффициентом скорости.Обозначим через  (расчетный напор) величину:  . После подстановки указанных выражений в формулу для скорости, vC, получим . (5.6)Обычно коэффициент скорости принимает значения = 0,97…0,98 ( = 0,06). В случае истечения идеальной жидкости = 0, = 1,0 и теоретическая скорость истечения равна  .Таким образом, коэффициент есть отношение действительной скорости истечения к теоретической: . (5.7)Действительная скорость истечения всегда меньше теоретической за счет сопротивления, следовательно, коэффициент всегда меньше 1,0.Расход жидкости найдем как произведение действительной скорости истечения на фактическую площадь сечения струи:  . (5.8)Подставив в формулу (5.8) выражения для  из формулы (5.1) и из формулы (5.6) получим: , (5.9)где – площадь отверстия;  – коэффициент сжатия струи.Произведение и принято обозначать буквой  и называть коэффициентом расхода: . (5.10)Окончательно выражение для расхода жидкости запишется в виде  . (5.11)Полученное выражение является основным для данного раздела. Оно решает основную задачу – определяет расход. Применимо для всех случаев истечения. Экспериментально установлено, что значение коэффициента колеблется в пределах 0,59…0,63, составляя в среднем 0,61. Из уравнения (5.11) следует, что  . Это значит, что коэффициент расхода есть отношение действительного расхода к теоретическому, т.е. к тому расходу, который имел бы место при отсутствии сжатия струи и сопротивления.Следует иметь в виду, что  не есть расход при истечении идеальной жидкости, т.к. сжатие струи будет иметь место и при отсутствии гидравлических потерь.5.2. Истечение жидкости через затопленное отверстие Если пространство, куда вытекает жидкость, заполнено этой же жидкостью, то такое истечение называется истечением через затопленное отверстие или истечением под уровень. Возьмем два сосуда (рис. 5.4). В общей для двух сосудов стенке выполнено малое отверстие. Плоскость сравнения О–О проведем через центр тяжести отверстия. Давления на свободной поверхности обозначим через  и  . В частном случае они могут быть равны атмосферному  . Выберем сечение 1–1 на свободной поверхности и 2–2 – через сжатое сечение струи. Рис. 5.4. Истечение через затопленное отверстие Запишем уравнение Бернулли для выбранных сечений 1–1 и 2–2:  , (5.12)где – геометрическая высота сечения 1–1, ; – давление в сечении 1–1,  ; – скорость жидкости в сечении 1–1, = 0; – коэффициент Кориолиса в сечении 1–1, = 1,0; – геометрическая высота сечения 2–2, = 0;  – давление в сечении 2–2,  , здесь  – глубина расположения сечения 2–2 от свободной поверхности второго сосуда;  – скорость жидкости в сжатом сечении,  ; – коэффициент Кориолиса в сечении 2–2,  ;  – потери напора в местном сопротивлении (малом отверстии),  , здесь – коэффициент местного сопротивления малого отверстия.После подстановки получим уравнение Бернулли в виде  ,или  . (5.13)Откуда найдем  : . (5.14)Обозначим через  коэффициент скорости, а через  – расчетный напор.Получим  . (5.15)Расход жидкости определяется по формуле  . (5.16)где – коэффициент расхода жидкости через малое отверстие.Таким образом, имеем те же расчетные формулы, что и при течении жидкости в атмосферу, только расчетный напор в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход не зависят от высоты расположения отверстия в стенке сосуда. Значения коэффициента скорости , сжатия струи , расхода для малого затопленного отверстия в тонкой стенке практически не отличаются от соответствующих коэффициентов для незатопленного отверстия.Истечение жидкости из больших прямоугольных отверстий с тонкой стенкой при постоянном напоре При истечении жидкости через большие прямоугольные отверстия (рис. 5.5) напор в отдельных сечениях является переменной величиной, изменяясь от  в верхней части до в нижней части.Для определения расхода жидкости разобьем площадь сечения прямоугольного отверстия на горизонтальные полоски высотой 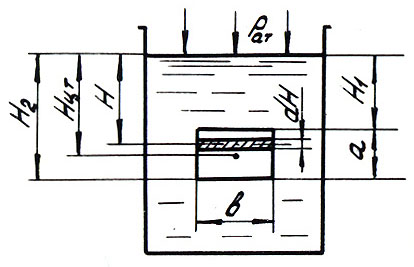 , каждую из которых можно рассматривать как малое отверстие с постоянным расходом и напором. Рис. 5.5. Истечение через большое прямоугольное отверстие Элементарный расход жидкости через малое прямоугольное отверстие запишется таким образом:  , (5.17)где  – ширин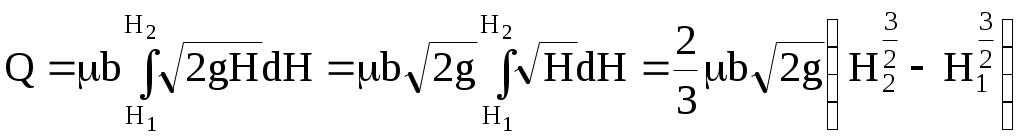а отверстия;  – расстояние до центра тяжести прямоугольной полоски (напор); – коэффициент расхода. Принимая  , найдем расход жидкости  через отверстие, интегрируя выражение для  в границах от до , получим: , (5.18)Или  , (5.19)где  – коэффициент расхода большого отверстия, определяется опытным путем.Обозначим напор до центра тяжести отверстия через Нц.т и выразим напоры , через Нц.т, получим  ;  .После преобразования формулы (5.19) с учетом выражений для и можно получить приближенное выражение для определения расхода жидкости через большое прямоугольное отверстие. . (5.20)5.4. Истечение жидкости через насадки Насадком называют короткую трубу, присоединенную к отверстию в тонкой стенке. Длина насадка равна трем–шести диаметрам отверстия, т.е.  = (3…6) .По форме насадки бывают (рис. 5.6): внешние цилиндрические (I тип), внутренние цилиндрические (II тип), конические сходящиеся (III тип), конические расходящиеся (IV тип), коноидальные (V тип). Расход жидкости через насадок определяется по формуле расхода через малое отверстие в тонкой стенке, где коэффициент расхода принимают в зависимости от формы насадок.Насадки типов I, II, IV применяют для увеличения пропускной способности отверстия. Насадки типов III, V применяют для изменения кинетической энергии струи.  Рис. 5.6. Типы насадков В табл. 5.1 приведены численные значения коэффициентов расхода , скорости , сжатия и сопротивления для насадков различных типов.Таблица 5.1
5.5. Истечение жидкости при переменном напоре (опорожнение сосудов) При переменном напоре истечения жидкости через отверстия и насадки имеет место неустановившееся движение жидкости. Однако если изменение напора, а следовательно, и скорость истечения происходит медленно, можно с достаточной для практических целей точностью принять законы установившегося движения. То есть можем принять уравнение Бернулли для установившегося движения жидкости. Расчет опорожнения сосуда заключается в определении времени этого процесса. Рассмотрим сосуд с жидкостью с отверстием в донной части (рис. 5.7). 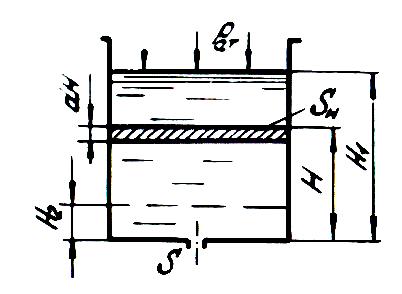 Рис. 5.7. Истечение жидкости при переменном напоре Обозначим через Н переменную высоту уровня жидкости в сосуде, отсчитываемую от дна в момент времени  ;  – площадь сечения резервуара на этом уровне; – площадь отверстия. Начальная высота жидкости в сосуде обозначается через , конечная – через . Взяв бесконечно малый промежуток времени  , запишем следующее уравнение объемов: , (5.21)где – снижение уровня жидкости в сосуде за время .Знак минус в формуле обусловлен тем, что положительному приращению времени соответствует отрицательное приращение уровня жидкости . Из уравнения (5.21) найдем : . (5.22)Время истечения жидкости с уровня до определится следующим образом (при ): . (5.23)Интеграл может быть подсчитан, если известен закон изменения площади по высоте. Рассмотрим частный случай, когда площадь поперечного сечения сосуда постоянна по высоте, т.е. .В этом случае время истечения определяется по формуле  . (5.24)Найдем время полного опорожнения сосуда, т.е. когда = 0.Получим  , (5.25)или  , (5.26)где  – объем сосуда;  – максимальный расход жидкости при начальном напоре .Время истечения того же объема жидкости при постоянном напоре равно . (5.27)Сравнив формулы (5.26) и (5.27) , можно сделать вывод о том, что время опорожнения сосуда при переменном напоре в два раза больше времени истечения того же объема жидкости при постоянном напоре. 5.6. Гидравлические струи жидкости Поток жидкости, не ограниченный твердыми стенками, называется струей жидкости. Различают затопленные струи и незатопленные струи. Затопленной струей называется струя, окруженная жидкостью. Незатопленной свободной струей жидкости называется струя, окруженная газом, в частности воздухом. К этим струям относятся водяные струи: пожарные, фонтанные струи, гидромониторные, дождевальные и др. 5.6.1. Структура струи Рассмотрим структуру затопленной струи. Вылетая из специального насадка при очень больших скоростях и давлениях, гидравлическая струя имеет свою определенную структуру. Рассматривая струю, мы должны различать ее границу, т.е. поверхность раздела, отделяющую саму струю от окружающей среды. На рис. 5.8 представлена структура затопленной струи. Струя – это конус, образующие которого пересекаются в точке О, называемой полюсом. Сечение I–I, совпадающее с выходным сечением насадка, называется начальным сечением. У начального сечения I–I скорости по сечению струи почти одинаковые. На расстоянии  – распределение скоростей типичное для однородного потока. Сечение II–II называется переходным.Участок длиной между сечениями I–I и II–II называется начальным участком.Если до переходного сечения скорость на оси струи постоянна, то начиная от переходного сечения, эта скорость вдоль оси потока падает. Участок за переходным сечением (II–II) называется основным. Основной участок (II–II – III–III) характеризуется компактностью струи, уменьшением скорости на оси струи, уменьшением пропорционально длине поля скоростей. Конечный участок – после сечения III–III, где струя распадается. 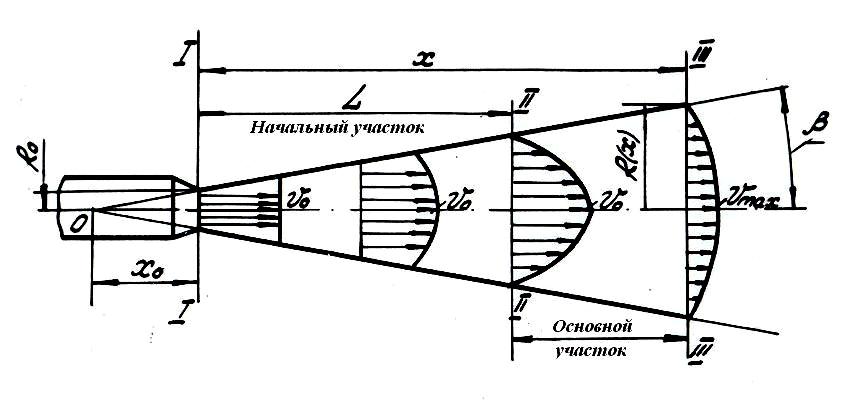 Рис. 5.8. Структура затопленной струи Практический интерес представляют величины, определяющие изучаемую струю: - расстояние  , дающее положение полюса струи;- длина начального участка; угол  , равный половине угла расхождения прямолинейных лучей, ограничивающих струю;- радиус  струи на заданном расстоянии  от начального сечения;- скорость  на оси основного участка струи.Все эти величины могут быть найдены по формулам, имеющимся в технической литературе, например, по формулам Г.Н.Абрамовича. В эти формулы, кроме радиуса насадка  , скорости истечения из отверстия  , входит экспериментальный коэффициент а, называемый коэффициентом структуры. Он учитывает структуру потока в выходном сечении.5.6.2. Сила давления струи на твердую преграду Основной задачей при рассмотрении взаимодействия струи с различными твердыми преградами является определение силы давления струи на эти преграды. Рассмотрим взаимодействие струи, вытекающей из насадка (  ), с твердой стенкой конической формы и осью, совпадающей с осью насадка (рис. 5.9). Рис. 5.9. Взаимодействие струи с твердой стенкой Струя жидкости, вытекающая из насадка, достигнув стенки, разбивается на два равных потока, движущихся со скоростями, равными скорости жидкости в гидравлической струе. Для определения величины силы давления  выделим из струи объем жидкости, заключенный между сечениями 1–1, 2–2 и 3–3, и применим закон об изменении количества движения.Примем следующие допущения: весом жидкости, разницей высот точек в сечениях 2–2, 3–3 пренебрегаем; потери жидкости на гидравлическое трение между сечениями 1–2 и 1–3 отсутствуют. Сформулируем теорему об изменении количества движения применительно к рассматриваемому случаю. Изменение количества движения за время  в рассматриваемом объеме жидкости будет равно разности количества движения массы жидкости  , имеющей скорость  , и вошедшей за время через сечение 1–1, и масс жидкости  и  , вышедших за время через сечения 2–2 и 3–3 из данного объема со скоростями и  .Теорема об изменении количества движения в проекции на горизонтальную ось записывается следующим образом:  , (5.28)где – сила давления струи на стенку; – масса жидкости, проходящая со скоростью через сечение 1–1 за время ; , – массы жидкости, проходящие соответственно через сечения 2–2 и 3–3 со скоростями , , = = ; = = ввиду деления гидравлической струи на два разных потока.Запишем уравнение (5.28) с учетом того, что = = и = = : ,или  . (5.29)Откуда сила давления определится по формуле  . (5.30)Массу жидкости можно записать следующим образом:  , (5.31)где  – плотность жидкости; – расход жидкости.С учетом формулы (5.31) выражение для силы давления окончательно запишется следующим образом:  . (5.32)Учитывая, что  , а  , можно записать следующее выражение: . (5.33)При угле  = 90о, т.е. при действии струи на плоскую стенку,  = 0 и  . (5.34) Рис. 5.10. Воздействие струи на преграду ( = 180о)Если преграда имеет форму, при которой струя будет поворачиваться на угол = 180о (рис. 5.10), то сила будет равна , (5.35)т.е. в два раза больше, чем при действии на плоскую стенку. | |||||||||||||||||||||||||||||||||||||||
= 13о24
5…7о