Составление алгоритмов. ПР. 5. Найти сумму и количество чисел, кратных 9, в диапазоне от 0 до 50
 Скачать 15.57 Kb. Скачать 15.57 Kb.
|
|
Вариант 1 Составить алгоритм решения задач, используя основные алгоритмически конструкции. Каждый алгоритм должен содержать три этапа: 1. Постановка задачи; 2. Анализ решения; 3. Блок-схема алгоритма. 1. Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a•b•c и площадь поверхности S = 2•(a•b + b•c + a•c). 2. Дана площадь S круга. Найти его диаметр D и длину L окружности, ограничивающей этот круг, учитывая, что L = 2•π•R, S = π•R2 . В качестве значения π использовать значение 3.14. 3. Дано четырёхзначное число. В нем зачеркнули вторую слева цифру и приписали ее в конце. Найти полученное число. 4. Если среди трех чисел a, b, c имеется хотя бы одно четное, то найти максимальное число, иначе – минимальное. 5. Найти сумму и количество чисел, кратных 9, в диапазоне от 0 до 50. 6. Напишите алгоритм, который в последовательности натуральных чисел определяет сумму трёхзначных чисел, кратных 4. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число: сумму трёхзначных чисел, кратных 4. Вариант 2 Составить алгоритм решения задач, используя основные алгоритмически конструкции. Каждый алгоритм должен содержать три этапа: 1. Постановка задачи; 2. Анализ решения; 3. Блок-схема алгоритма. 1. Даны катеты прямоугольного треугольника a и b. Найти его гипотенузу c и периметр P: 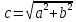 , P = a + b + c. , P = a + b + c.2. Дана длина L окружности. Найти ее радиус R и площадь S круга, ограниченного этой окружностью, учитывая, что L = 2•π•R, S = π•R2 . В качестве значения π использовать значение 3.14. 3. Дано четырёхзначное число. В нем зачеркнули вторую справа цифру и приписали ее в начале. Найти полученное число. 4. Если среди трех чисел a, b, c имеется хотя бы одно нечетное, то найти минимальное число, иначе – максимальное. 5. Найти произведение четных чисел в диапазоне от 2 до 30. 6. Напишите алгоритм, который в последовательности целых чисел определяет количество чисел, кратных 5 или 9. Программа получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чисел, кратных 5 или 9. Вариант 3 Составить алгоритм решения задач, используя основные алгоритмически конструкции. Каждый алгоритм должен содержать три этапа: 1. Постановка задачи; 2. Анализ решения; 3. Блок-схема алгоритма. 1. Дано значение температуры T F в градусах Фаренгейта. Определить значение этой же температуры в градусах Цельсия. Температура по Цельсию T C и температура по Фаренгейту T F связаны следующим соотношением: T C = (T F − 32)•5/9. 2. Дана длина L окружности. Найти ее радиус R и площадь S круга, ограниченного этой окружностью, учитывая, что L = 2•π•R, S = π•R2 . В качестве значения π использовать значение 3.14. 3. Дано четырёхзначное число. Найти число, полученное при перестановке первой и третьей цифр заданного числа. 4. Если среди трех чисел a, b, c имеется хотя бы одно число кратное 3, то найти максимальное число, иначе – минимальное. 5. Найти произведение первых двадцати нечетных чисел, кратных 8. 6. Напишите алгоритм, который в последовательности натуральных чисел определяет количество чисел, кратных 6 и оканчивающихся на 4. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чисел, кратных 6 и оканчивающихся на 4. Вариант 4 Составить алгоритм решения задач, используя основные алгоритмически конструкции. Каждый алгоритм должен содержать три этапа: 1. Постановка задачи; 2. Анализ решения; 3. Блок-схема алгоритма. 1. Даны координаты трех вершин треугольника: (x1, y1), (x2, y2), (x3, y3). Найти его периметр и площадь, используя формулу для расстояния между двумя точками на плоскости (см. задание Begin20). Для нахождения площади треугольника со сторонами a, b, c использовать формулу Герона: S =  , , где p = (a + b + c)/2 – полупериметр. 2. Дана площадь S круга. Найти его диаметр D и длину L окружности, ограничивающей этот круг, учитывая, что L = 2•π•R, S = π•R2 . В качестве значения π использовать значение 3.14. 3. Дано четырёхзначное число. Найти число, полученное при перестановке второй и третьей цифр заданного числа. 4. Если среди трех чисел a, b, c имеется хотя бы одно число оканчивающееся на 7, то найти минимальное число, иначе –максимальное. 5. Найти сумму первых десяти натуральных чисел, кратных 5. 6. Напишите алгоритм, который в последовательности целых чисел определяет количество чётных чисел, кратных 7. Программа получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чётных чисел, кратных 7. |
