лекция. Лекция 5. 5 основы биомеханического контроля (2 часа)
 Скачать 449.63 Kb. Скачать 449.63 Kb.
|
|
1.4. Биомеханика передвижений с механическими преобразователями движения К механическим преобразователям движения относятся различные средства биотранспорта (по терминологии В.В. Тимошенкова) и гребные устройства. Под биотранспортом понимают устройства, имеющие специальный механизм – велопривод, с помощью которого мускульная энергия человека преобразуется в его передвижение вместе с устройством. В число устройств биотранспорта входят велосипеды, веломобили, водные велосипеды, мускулолеты. Наиболее распространенной и наиболее изученной локомоцией с точки зрения биомеханики двигательных действий является педалирование на велосипеде. Педалирование как процесс вращения шатунов велосипеда является результатом трех одновременно совершаемых вращательных движений звеньев нижних конечностей велосипедиста (рисунок 5.8): − бедра вокруг оси, проходящей через тазобедренный сустав; − голени относительно коленного сустава; − стопы относительно голеностопного сустава.  Рисунок 5.8 - Оси и направления вращения сегментов ног при педалировании на велосипеде (по Hay) Эффективность двигательных действий велосипедиста зависит от посадки и техники педалирования. Посадкой называют позу гонщика на велосипеде. В зависимости от наклона туловища различают низкую, среднюю и высокую посадку. Чем ниже посадка, тем горизонтальнее расположено туловище и тем меньше модель (т.е. наибольшая величина площади сечения, перпендикулярного воздушному потоку). Следовательно, меньше и сила лобового сопротивления воздуха. Поэтому гонщики, как правило, применяют низкую посадку. Но при низких скоростях (например, при езде на велосипеде в оздоровительных целях) привычнее и удобнее средняя и высокая посадка. В то же время посадка велосипедиста не должна мешать работе внутренних органов. Посадка велосипедиста на подъеме может быть такой: 1) кисти рук на тормозных рычагах; 2) кисти в центре руля, обхватывают его снизу; 3) положение, при котором переносится ОЦТ тела. При педалировании центры тяжести левой и правой ноги движутся по круговым траекториям, а вот совместный центр тяжести двух ног практически не перемещается относительно велосипеда. Из этого следует, что при езде по горизонтальной поверхности вертикальные перемещения ОЦТ практически отсутствуют и, следовательно, работа, направленная на вертикальные перемещения тела, близка к нулю. При педалировании целесообразно, чтобы и правая, и левая нога в каждый момент времени создавали положительный (продвигающий вперед) момент силы. Это неосуществимо при импульсном педалировании и возможно при круговом педалировании при наличии специальных приспособлений – туклипсов и велошипов. Туклипсы необходимы для подтягивания педали вверх, а шипы – для ее проводки, т.е. перемещения назад и вперед. Совместное действие мышц в режиме, близком к изометрическому, позволяет хорошо подготовленному велосипедисту развить силу 2500 – 3500 Н, а при проводке и подтягивании – 800 – 1100 Н (В.Л. Уткин, 1989). При езде на велосипеде приходится преодолевать три силы сопротивления: − силу лобового сопротивления; − силу трения качения; − сталкивающую силу при подъеме в гору. Внешним силам сопротивления спортсмен противопоставляет силу своих мышц, правильную посадку, экипировку и т.д. Главное препятствие для преодоления дистанции – сила сопротивления воздуха, которая зависит от следующих факторов: − [S] – величины поверхности сопротивления, которую можно изменить посадкой; − [C] – коэффициент сопротивления, который зависит от обтекаемости фигуры велосипедиста и величины поверхности одежды; − [ρ] – плотность воздуха, которая на равнине примерно постоянна, а в горных равнинах несколько ниже; − [ν2] – квадрат скорости. При встречном ветре сила сопротивления воздуха увеличивается, а при попутном – уменьшается. На скорость перемещения велосипедиста влияет сила трения качения (трение шин о покрытие шоссе). Чем тяжелее велосипедист, тем больше трение качения, а также чем толще шины и меньше они накачаны – тем больше трение качения. Влияют на скорость велосипедиста также качество покрытия шоссе, размер колес. Сила трения качения [Fкач] зависит от следующих факторов: − [N] – сила нормального давления – соответствует весу спортсмена с велосипедом, если он направлен перпендикулярно к поверхности, по которой происходит перемещение; − [r] – радиус колес; − [b] – расстояние между теоретической точкой опоры шины и фактической точкой встречи шины с поверхностью, по которой происходит перемещение. Во время подъема скорость небольшая, решающую роль приобретает сталкивающая сила, а сопротивлением встречного воздушного потока можно пренебречь. Для сталкивающей силы [Fc] решающими являются следующие факторы: − [G] – суммарный вес спортсмена с велосипедом; − [l] – длина пути; − [h] – высота подъема на 100 м пути. 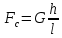 (5.2) (5.2)При выполнении поворота возникает центробежная сила, величина которой зависит от трех факторов: − чем больше скорость и вес спортсмена с велосипедом и чем меньше радиус закругления, тем больше центробежная сила; − для противодействия центробежной силе следует наклониться вместе с велосипедом в сторону закругления. На рисунке 5.9 показаны центробежная сила и направление взаимодействия других сил, возникающих при прохождении виража; − в зависимости от формы виража и скорости необходимо наклониться так, чтобы угол между велосипедом и поверхностью трека составлял от 700 до 1100. В идеальном варианте он должен быть равен 900. Но в некоторых ситуациях гонщик должен ехать по треку медленно, например, в спринте, парной групповой гонке и т.д. В этих случаях при слишком маленькой скорости можно упасть, т.к. колесо соскользнет вниз. При медленной езде или попытке полностью остановиться центробежные силы незначительны или даже равны нулю, а значит наклоняться на вираже нельзя. Чем тяжелее спортсмен и чем выше располагается он на вираже, тем больше сталкивающая сила. Преимущество будет на стороне гонщика, если при выходе из финишного виража он окажется в верхней его части на одном уровне с соперником (Дубровский В.И., 2008). 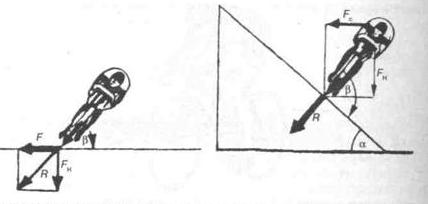 Рисунок 5.9 - Силы, действующие на велосипедиста при прохождении виража: [F] – центробежная сила, [Fн] – сила нормального давления, [R] – результирующая, [α] – угол крутизны трека, [Fс] – сталкивающая сила, [β] – угол наклона Эффективность езды на велосипеде зависит от частоты вращения педалей и выбора передачи. Чем больше передача, тем выше силы действия на педали и больше укладка – расстояние, преодолеваемое за один оборот педалей. При выборе режима педалирования следует учитывать индивидуальные особенности спортсмена и внешние условия. Чем ниже физическая работоспособность, значительнее утомление и сложнее условия (плохое покрытие дороги, встречный ветер и т.д.), тем выше оптимальный темп и меньше оптимальная передача. Вопрос 2. Биомеханические основы прыжков В прыжках расстояние преодолевается полетом. При этом достигается либо наибольшая длина прыжка (прыжок в длину с разбега, тройной прыжок), либо наибольшая высота (прыжок в высоту с разбега, прыжок с шестом), либо значительные и длина, и высота (опорный прыжок в гимнастике). Траектория ОЦТ тела спортсмена в полете определяется формулами: 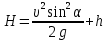 (5.3) (5.3) 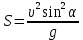 (5.4) (5.4) где [S] – длина и [h] – высота траектории ОЦТ (без учета его высоты в моменты вылета и приземления); [𝜐] – начальная скорость ОЦТ в момент вылета; [α] – угол наклона вектора скорости к горизонтали в момент вылета; [g] – ускорение свободно падающего тела. Как видно из формул, особенно важны величина начальной скорости ОЦТ и угол его вылета. Начальная скорость ОЦТ создается при отталкивании, а также при подготовке к нему. Таким образом, в спортивных прыжках различается подготовка к отталкиванию, отталкивание от опоры, полет и амортизация (после приземления). В подготовку входят разбег и подготовительные движения на месте отталкивания. Разбег. В разбеге решаются две задачи: − создание необходимой скорости к моменту прихода на место отталкивания; − создание оптимальных условий для опорного взаимодействия. Структура разбега, т.е. особенности достижения скорости, ритм, соотношение длины шагов в прыжках в длину и высоту, отличается. В прыжках в длину прыгун начинает разбег с максимальной частотой шагов, постепенно увеличивая длину шагов (как в спринте при беге с высокого старта). Главная задача разбега в прыжках в длину – набрать максимально возможную скорость. В прыжках в высоту прыгун начинает разбег максимально длинными шагами, постепенно повышая темп движений. Главная задача разбега в прыжках в высоту – подготовиться к отталкиванию, поэтому последние шаги разбега выполняются с вертикальным положением туловища, даже с его отклонением назад, что приводит к снижению скорости разбега. При подготовке к отталкиванию в разбеге в прыжках в высоту необходимо отвести руки назад для последующего одновременного маха и более быстрого движения таза (по отношению к плечам) на последних трех шагах разбега. В прыжках в длину и в тройном подготовка к отталкиванию сводится к понижению ОЦТ на последних шагах за счет сильного сгибания ног в коленных суставах в опорных фазах и уменьшения длины последнего шага. Точность разбега достигается за счет: 1) стандартного исходного положения в начале разбега; 2) стабильного выполнения первых шагов разбега; 3) устойчивого ритма последних шагов разбега. Наибольшее значение точность разбега имеет для прыжков в длину и в тройном, т.к. непосредственно влияет на результат (результат не засчитывается при заступе за планку). Отталкивание. Отталкивание от опоры в прыжках совершается за счет выпрямления толчковой ноги, маховых движений рук и туловища. Цель отталкивания – изменение направления движения ОЦТ тела. Это наиболее важная и характерная фаза прыжков. Во время отталкивания нога ставится впереди проекции ОЦТ и испытывает значительную нагрузку, величина которой зависит от скорости тела в момент постановки ноги на отталкивание, массы тела прыгуна и угла наклона ноги. Чем больше скорость и масса, а угол постановки ноги меньше, тем большую нагрузку испытывает нога. Под действием этой нагрузки при отталкивании нога сгибается в суставах. Часть отталкивания от момента постановки ноги до момента наибольшего сгибания в суставах принято называть фазой амортизации, а часть отталкивания от момента наибольшего сгибания опорной ноги в суставах до момента отрыва ноги от опоры – фазой активного отталкивания. Особенности выполнения отталкивания определяются угловыми характеристиками в моменты постановки ноги, окончания амортизации, отрыва ноги от опоры. При отталкивании опорные звенья неподвижны относительно опоры, а подвижные звенья под действием тяги мышц передвигаются в общем направлении отталкивания. На стопу как на опорное звено со стороны голени действует давление ускоряемых звеньев тела, направленное назад и вниз. Через стопу оно передается на опору. Противодействием этому давлению служит реакция опоры. Она приложена к стопе в направлении вперед и вверх. Реакция опоры и давление голени приложены к стопе в противоположных направлениях; они взаимно уравновешиваются и фиксируют стопу на опоре. Силы мышечных тяг толчковой ноги выпрямляют ее. Поскольку стопа фиксирована на опоре, голень и бедро передают ускоряющее воздействие отталкивания через тазобедренный сустав остальным звеньям тела. При ускоренном движении подвижных звеньев на них воздействуют тормозящие силы (тяжести и инерции) других звеньев, а также силы сопротивления мышц-антагонистов. Следовательно, звенья тела получают ускорение вследствие того, что имеются движущие силы, действие которых превышает сопротивление тормозящих сил. Чтобы ОЦТ изменил движение, необходимо (в соответствии с законом сохранения количества движения) наличие внешней силы приложенной к системе. Реакция опоры при отталкивании как раз и является такой необходимой внешней силой. Отталкивание в прыжках сопровождается маховыми движениями рук и свободной ноги. Маховые движения оказывают значительное влияние на отталкивания за счет: а) перераспределения количества движения; б) увеличения инерционного давления на мышцы толчковой ноги в момент окончания фазы амортизации (это способствует более сильному сокращению мышц); в) повышения ОЦТ во время отталкивания. Эффективность маховых движений зависит от согласованности и своевременности маха рук и ног. Особенности выполнения маховых движений могут влиять на скорость отталкивания: например, выполнение махового движения прямой ногой замедляет отталкивание, а согнутой – ускоряет. В прыжках в высоту маховые движения выполняются, как правило, одновременно двумя руками, а в прыжках в длину, как в беге, но с большей амплитудой. Отталкивание заканчивается полным выпрямлением толчковой ноги, при этом угол отталкивания (угол, образованный осью ноги и горизонтальной плоскостью в момент отрыва от опоры) в прыжках в высоту составляет 90°, а в прыжках в длину – 70–800. Бедро маховой ноги в момент отрыва от опоры поднимается до горизонтали в прыжках в длину и несколько выше в прыжках в высоту (это зависит от способа выполнения махового движения). Полет. Цель полета различна в прыжках в длину и высоту. Если в прыжках в длину цель полета – сохранить равновесие тела и подготовиться к приземлению, то в прыжках в высоту и с шестом – создать оптимальные условия для преодоления планки. После завершения отталкивания начинается фаза полета, в которой ОЦТ описывает определенную траекторию, зависящую от угла вылета и начальной скорости. Изменить эту траекторию прыгун не в состоянии, однако за счет соответствующих двигательных действий он может изменить расположение тела и его отдельных частей относительно ОЦТ. При этом перемещение некоторых частей тела в одном направлении вызывает компенсаторные движения его других частей в противоположном. В прыжках в высоту и с шестом спортсмену необходимо учитывать эти закономерности при переходе через планку, так как в некоторых случаях можно добиться такого положения, что прыгун, огибая планку, может пронести свой ОЦТ тела под ней. Поэтому спортсмену выгоднее переносить через планку тело не сразу, а последовательно, чтобы за счет активного опускания одних частей тела переносить другие. В прыжках в длину и тройным движения в полете позволяют сохранить устойчивое положение и создают благоприятные предпосылки для рационального приземления. Приземление. Значение приземления и характер его выполнения не одинаковы в различных видах прыжков. В прыжках в высоту и с шестом эта фаза уже никакого влияния на результат не оказывает, поэтому основное ее назначение – обеспечить безопасность спортсмена. В прыжках в длину и тройным, кроме обеспечения безопасности, способ приземления оказывает значительное влияние на результат. В связи с этим прыгунам необходимо стремиться, чтобы при приземлении пятки прыгуна коснулись грунта впереди точки приземления ОЦТ или совпадали с ней. Если точка приземления будет находиться сзади точки приземления ОЦТ, то это ухудшит результат. Если уже точка приземления будет находиться далеко впереди точки приземления ОЦТ, то спортсмен может упасть назад и ухудшить результат. Оптимальное расположение точки приземления достигается за счет одновременного выпрямления ног в конце полета, отведения рук назад и небольшого наклона туловища вперед. Во время приземления организм спортсмена испытывает хоть и кратковременную, но значительную нагрузку. Замедление движения происходит как за счет амортизационного сгибания в тазобедренных, коленных и голеностопных суставах, так и за счет деформации места приземления. С целью уменьшения напряжения мышц и профилактики травматизма спортсменам рекомендуется удлинять путь торможения тела при приземлении. Вопрос 3. Биомеханические основы перемещающих движений Перемещающими называются движения, в результате которых происходит перемещение человеком какого-либо тела. 3.1. Закономерности полета спортивных снарядов В значительном количестве видов спорта результат определяется либо по перемещению снаряда определенной формы и веса на максимальное расстояние (толкание ядра, метание копья, молота и диска), либо по попаданию снаряда в определенное место или зону пространства (спортивные игры, стрельба). В обоих случаях важнейшее значение имеет учет закономерностей, в соответствии с которыми происходит полет спортивных снарядов в пространстве. Рассмотрим особенности полета тел в чистом виде, т.е. при отсутствии сопротивления со стороны окружающей среды. Закон движения ОЦТ брошенного в плоскости ХОУ под углом к горизонту тела определяется уравнениями динамики, учитывающими, что по вертикали действует сила тяжести, а по горизонтали внешних сил нет. Уравнения движения тела для такого случая выглядят следующим образом: max = 0, (5.5) may = mg, (5.6) где [m] – масса тела; [ax] и [ay] – горизонтальное и вертикальное ускорение. Предположим, что в момент начала полета тело имело скорость [ν], направленную под углом [α] к горизонтали, и находилось на высоте [h0] от поверхности опоры. Решением системы уравнений являются следующие соотношения: OX = ν·cosα·t, (5.7) OY = h0 + ν·sinα ·t – gt2/2, (5.8) где [t]– текущее время, отсчитанное от начала движения. Анализ приведенных соотношений показывает, что перемещение по горизонтали (дальность полета) зависит не только от горизонтальной скорости, но и от времени нахождения тела в полете. Последнее зависит от вертикальной скорости тела в момент вылета. Время полета находится из второго уравнения последней системы, в которое подставляется условие соприкосновения тела с опорой в конце полета (OY = 0). Так, используя данное условие, имеем обыкновенное квадратное уравнение, общим решением которого будет следующее выражение: 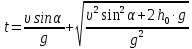 , (5.9) , (5.9) Дальность полета определяется из первого уравнения системы при подстановке в него полученного времени полета: 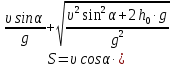 (5.10) (5.10)Анализ полученной формулы показывает, что дальность полета тела определяется тремя параметрами: значением скорости, сообщенной снаряду, углом вылета и высотой точки вылета. Наибольшее влияние на пролетаемое телом расстояние оказывает величина скорости вылета. Так, ее увеличение на 5% по отношению к исходному значению 10 м/с при постоянных значениях остальных двух параметров (например, α=450 и h0=1 м) вызывает соответствующее увеличение дальности полета приблизительно на 1 м. Оптимальным углом вылета спортивного снаряда при условии, что в момент вылета он расположен на поверхности земли (h0=0), является угол α=450. При наличии исходной высоты он несколько уменьшается. Так, при h0=1 м оптимальный угол вылета составляет 420, а при h0=1,5 м – 410. Учет силы сопротивления окружающей среды несколько изменяет описанную выше картину движения спортивного снаряда. При этом действие сил со стороны окружающей среды проявляется по нескольким направлениям. Так, на движущееся тело действует сила лобового сопротивления, подъемная сила (при расположении оси симметрии тела под углом к скорости движения ОЦТ или при движении несимметричного тела), а также силы, связанные с вращением тела относительно его ОЦТ во время полета (эффект Магнуса). Сила лобового сопротивления замедляет движение тела как в вертикальном, так и в горизонтальном направлениях. Результатом ее действия на полет спортивного снаряда является уменьшение дальности полета, по сравнению со случаем отсутствия сопротивления воздуха. Изменение высоты полета снаряда под действием сил сопротивления зависит от образования подъемной силы и влияния вращения тела. В случае снаряда типа ядра или молота действует только сила лобового сопротивления и в таком случае происходит постепенное замедление движения как по горизонтали, так и по вертикали. Учет действия подъемной силы (диск, копье) приводит к некоторому увеличению времени полета, поскольку при расположении продольной оси симметрии снаряда под углом к скорости движения ОЦТ (угол атаки) подъемная сила в некоторой степени компенсирует действие силы тяжести, уменьшая ускорение снаряда, направленное вниз. Поэтому пролетаемое расстояние, как правило, оказывается большим, чем при аналогичном перемещении симметричного тела с аналогичными исходными параметрами вылета, при отсутствии сопротивления воздуха. При анализе влияния сил, действующих со стороны окружающей среды, на дальность полета спортивного снаряда, следует учитывать их взаимную зависимость от угла атаки. Так, при нулевом значении указанного угла подъемная сила не образуется. При его увеличении происходит ее увеличение, вместе с тем изменяется площадь тела, перпендикулярная налетающему потоку воздуха, и, как следствие этого, возрастает сила лобового сопротивления. Например, для такого спортивного снаряда, как диск, существует оптимальное значение угла атаки, лежащее в пределах 25 – 300. При движении таких тел, как мячи, большое значение для дальности и высоты полета имеет их вращение относительно оси, проходящей через ОЦТ. В данном случае подъемная сила в виде, описанном выше, не возникает, поскольку мячи имеют симметричную форму (имеются в виду футбол, волейбол, теннис), однако вращение такого тела вызывает возникновение дополнительных сил, зависящих от его направления и угловой скорости. Механизм образования таких сил изображена на рисунке 5.10. 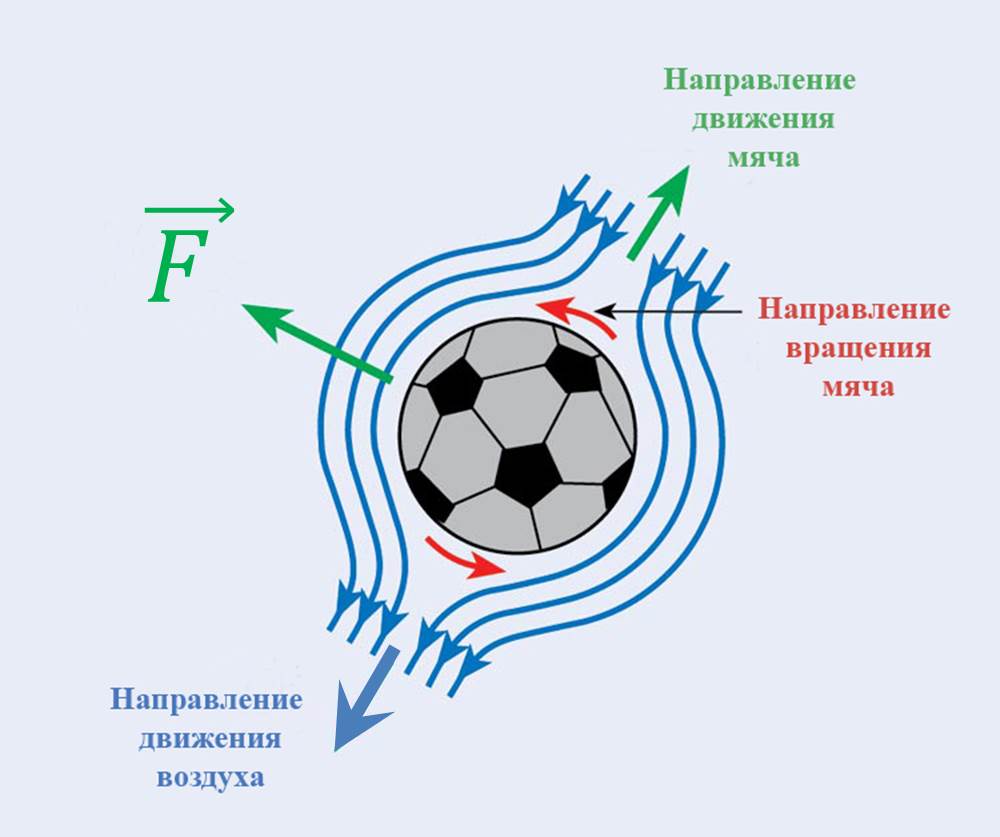 Рисунок 5.10 - Механизм образования дополнительных сил, связанных с вращением спортивного снаряда Представим, что мяч, находясь в полете, имеет вращение в направлении «против часовой стрелки». Перемещаясь в вязкой среде (в воздухе), мяч увлекает за собой частицы окружающей среды. Они как бы прилипают к поверхности мяча. При вращении мяча во время полета эти частицы участвуют в двух движениях: они перемещаются вместе с центром тяжести мяча и одновременно имеют линейную скорость вращения относительно его ОЦТ. При столкновении со встречным потоком воздуха снизу от мяча происходит некоторое замедление движения воздуха относительно ОЦТ мяча, поскольку налетающие частицы воздуха и частицы, увлекаемые мячом в ходе его вращения, имеют противоположные направления скорости. Сверху от мяча, в соответствии с описанными закономерностями, картина противоположна. Здесь скорость воздуха выше. По законам аэродинамики чем выше скорость воздушного потока, тем ниже в нем давление. Поэтому оказывается, что под мячом давление выше, чем над ним. Следствием этого является возникновение силы (в данном случае подъемной) в направлении от зоны высокого давления к зоне низкого. Возникновение такой силы, благодаря собственному вращению физического тела при перемещении в вязкой среде, называется эффектом Магнуса. Величина силы, связанной с вращением тела при движении, зависит от соотношения скорости набегающего потока и линейной скорости точек поверхности вращающегося тела. При этом, чем больше их разность, тем в большей степени проявляется эффект Магнуса. Образование дополнительных сил, связанных с вращением мяча, очень широко используется в теннисе, футболе и регби. Их следует учитывать при выполнении волейбольных ударов. В меньшей степени эффект Магнуса сказывается на движении баскетбольных мячей (из-за их более заметной массы). При выполнении удара по футбольному мячу можно обеспечить его вращение в различных плоскостях. При этом вращение в вертикальной плоскости позволяет (в зависимости от его направления) либо заставить мяч лететь выше и дальше, по сравнению с отсутствием вращения, либо резче падать вниз. Вращение мяча в горизонтальной плоскости приводит к соответствующему отклонению мяча от прямолинейного движения и искривляет его траекторию (крученые, обводящие удары) (Сотский Н.Б., 2002). 3.2. Сообщение движения спортивным снарядам При выполнении спортивных движений существует два способа сообщения скорости спортивным снарядам. Это – разгонперемещаемого объекта и удар. При разгоне скорость снаряда растет постепенно в течение конечного промежутка времени. Разгоном сообщается движение спортивному ядру, молоту, копью, диску, мячу при выполнении бросков в баскетболе, гандболе и в некоторых других случаях. При ударных взаимодействиях происходит изменение скорости в процессе очень коротких взаимодействий, для которых характерны значительные силы взаимодействия. Сообщение скорости спортивным снарядам путем удара характерно для волейбола, футбола, для некоторых хоккейных ударов. Кроме этого, следует учитывать ударный характер взаимодействия спортивных снарядов с опорой, игроками (Сотский Н.Б., 2002). Большинство движений, связанных с разгоном перемещаемых тел, выполняются с предварительным разгоном всего тела человека. Поэтому вращение звеньев в суставах будет обусловлено двумя механизмами: − действием моментов сил, создаваемых мышцами-сгибателями и мышцами-разгибателями; − движением самого сустава, т.е. движением оси вращения звена, что вызывает вращательное движение звена особенно при резкой остановке (например, на этом механизме построено такое вращательное движение, как «выхлест голени» при торможении коленного сустава маховой ноги в беге). Любое бросковое движение условно состоит из двух фаз. В первой фазе спортивный снаряд разгоняется в основном за счет действия ног. Во второй фазе разгон продолжается за счет действия мышц туловища и рук. Вторая фаза, дающая большее увеличение скорости снаряда, включает в себя последовательное возрастание угловых скоростей звеньев тела. В последовательности развития активности мышц различных звеньев тела проксимальные звенья начинают вращательное движение раньше дистальных. Затем проксимальные звенья начинают замедляться до того, как дистальные звенья достигли пика угловой скорости. Бросковое движение при проксимально-дистальной последовательности включения звеньев отличается тем, что скорость разгоняемого снаряда заметно не возрастает до последних этапов движения. Но она резко увеличивается к моменту выпуска снаряда, когда все предыдущие подготовительные движения звеньев обеспечивают хлестовое движение последнего контактирующего со снарядом звена. Последовательное вовлечение звеньев в работу, построенное на том, что проксимальное звено обгоняет дистальное, важно не только с точки зрения более эффективного растяжения мышц и их активации для разгона звеньев. Сгибание руки при замахе уменьшает момент инерции всей кинематической цепи, что по закону сохранения кинетического момента (момента количества движения) увеличивает угловую скорость вращения звена. Если задача бросания предмета требует точности (например, выполнение штрафного броска в баскетболе), движения в этом случае приближаются к плоскостным, а стратегия заключается в сведении к минимуму числа звеньев тела, участвующих в движении (Попов Г.И., 2005). При сообщении движения путем разгона спортивный снаряд может иметь одну или более точек взаимодействия с каким-либо звеном тела спортсмена. При выполнении разгона точки соприкосновения мяча и руки движутся с одинаковым ускорением и набирают одинаковую скорость. Движение мяча как целого зависит от направления ускорения точки контакта относительно ОЦТ. Так, при прохождении вектора ускорения через ОЦТ мяча последний набирает скорость при отсутствии вращательного движения относительно ОЦТ. Если же вектор ускорения упомянутой точки не проходит через ОЦТ мяча, сила взаимодействия мяча и руки (ее направление совпадает с направлением ускорения) образует момент относительно ОЦТ мяча, в результате действия которого, кроме ускорения, мяч получит вращательное движение тем большее, чем большее значение имеет указанный момент силы. Если при выполнении броска имеется не точечный контакт, а целая область взаимодействия мяча с рукой (например, бросок гандболиста), то мяч и звено, взаимодействующее с ним, можно считать единым целым и линейная скорость мяча будет определяться скоростью поступательного движения кисти, а угловая – угловой скоростью указанного звена в момент утраты контакта. При этом линейная и угловая скорости кисти, выполняющей бросок, определяются скоростью ОЦТ игрока, угловой скоростью вращения его тела как целого, а также угловыми скоростями звеньев, вращающихся при выполнении суставных движений. При сообщении движения спортивному снаряду путем удара, взаимодействие тел, как уже указывалось, происходит весьма кратковременно. При этом результат соударения тел в значительной мере зависит от соотношения их масс и направления скоростей в момент соприкосновения тел. В качестве примера рассмотрим ситуацию, представленную на рисунке 5.11. 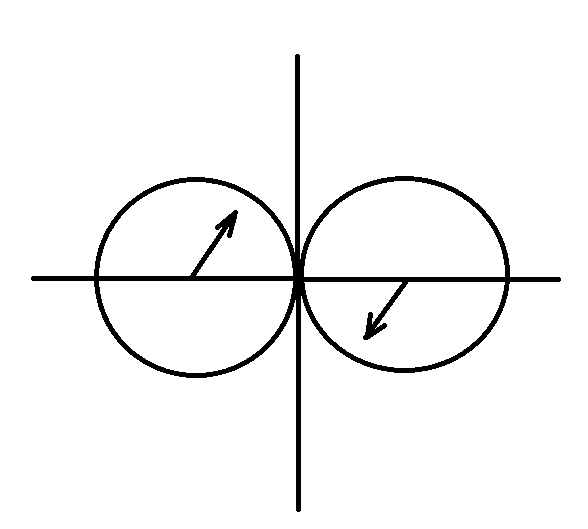 C G B A E D F υ2 υ1 Рисунок 5.11 - Характеристики ударного взаимодействия Предположим, что соударяющиеся тела с центрами тяжести А и В в момент удара контактируют в точке С. Проведем в последней касательную плоскость DE и линию FG, перпендикулярную к ней. Линия FG называется прямой удара. Если она проходит через центры тяжести соударяющихся тел, удар называется центральным. Если же хотя бы один из центров тяжести не лежит на указанной прямой, – нецентральным. Кроме этого, ударное взаимодействие тел может быть прямым или косым. В первом случае скорости центров тяжести в момент начала удара направлены вдоль прямой удара, а во втором – хотя бы одна из них имеет другое направление. На степень упругости взаимодействия двух тел при ударе оказывает значение коэффициент [k]. Ударное взаимодействие может быть: - абсолютно упругим ([k] = 1); - абсолютно неупругим ([k] = 0); - не вполне упругим (0 < [k] < 1). В первом случае кинетические энергии соударяющихся тел до удара и после него равны. Во втором – после удара тела имеют одинаковую скорость в направлении прямой удара (линия FG, см. рис. 5.11). Здесь тела, участвующие в прямом центральном ударе, не разлетаются, а продолжают двигаться вместе с одинаковой скоростью. При не вполне упругих ударах кинетическая энергия уменьшается в зависимости от величины коэффициента [k]. В природе практически всегда имеют дело с не вполне упругими ударами, иногда встречаются абсолютно неупругие. Абсолютно упругий удар – абстрактное понятие, в природе при движениях тел макроскопических размеров встречаются лишь приблизительно упругие удары, например, при соударении стальных шаров и в некоторых других ситуациях. Наиболее часто в спорте имеют место ударные взаимодействия, связанные с сообщением движения различного рода мячам. В таких ситуациях наиболее характерным является случай, когда взаимодействуют два тела со значительно отличающимися массами. Например, тело спортсмена и мяч при ударе футболиста или волейболиста; при соударении мяча или шайбы с поверхностью опоры, бортиком, штангой ворот. В случае, когда мяч приближается к опоре, имея скорость перпендикулярную к ее поверхности (прямой центральный удар), и его вращение относительно ОЦТ отсутствует, в процессе соударения не возникает сил, вызывающих отклонение направления вектора скорости от первоначального. После удара мяч отскочит, имея скорость в направлении, противоположном первоначальному. Величина скорости отскочившего мяча зависит от степени упругости взаимодействия. Степень упругости при реальных ударных взаимодействиях часто определяется коэффициентом восстановления, связанным с параметром [Kв] и представляющим собой отношение скоростей до и после удара и имеющим численное значение в пределах от 0 (при абсолютно неупругом ударе) до 1 (при абсолютно упругом). Коэффициент восстановления часто можно определить как квадратный корень из отношения высоты [h1] на которую тело отскочило после удара, к высоте [h0] , с которой оно было отпущено без начальной скорости: 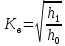 (5.11) (5.11) В случае ударного взаимодействия мяча с опорой при косом ударе поведение мяча после соударения с поверхностью зависит от степени упругости взаимодействия и наличия сил, действующих вдоль ударной плоскости (сил трения), а также, при наличии последних, и от скорости вращения мяча относительно его ОЦТ (Сотский Н.Б., 2002). Вопрос 4. Биомеханика движений вокруг осей 4.1. Вращательные движения тела при опоре Выполнение вращательных движений связано, прежде всего, с взаимодействием с опорой. Основное уравнение вращательного движения твердого тела: М = dL / dt, (5.12) где [M] – момент внешних сил относительно оси вращения; [L] – кинетический момент тела относительно оси вращения, равный произведению момента инерции тела на угловую скорость вращения относительно оси. В общем случае возникновение и изменение характера вращательного движения тела человека на опоре обусловлено действием момента внешних сил относительно оси вращения. Рассмотрим в качестве примера вращательное движение гимнаста вокруг перекладины из стойки на руках без изменения позы. Если пренебречь силой трения, то можно считать, что на гимнаста действует только сила тяжести, равная его весу и приложенная к ОЦТ. Плечом этой силы [d] является расстояние (радиус) [r] от ОЦТ до вертикали, проходящей через точку опоры, расположенную на продольной оси грифа перекладины. В исходном положении (стойка на руках) вертикальная проекция ОЦТ гимнаста проходит через точку опоры. Плечо силы тяжести в этот момент равно нулю. При выходе из положения равновесия плечо становится отличным от нуля, т.к. d = r·sinα, (5.13) где [α] – угол между вертикалью и радиусом. Относительно точки опоры, расположенной на оси вращения, возникает момент силы тяжести. Тело гимнаста начинает вращаться вокруг грифа перекладины с угловым ускорением, обратно пропорциональным величине его момента инерции относительно оси вращения. В процессе перемещения по окружности плечо силы тяжести начинает увеличиваться. Соответственно увеличиваются момент силы и угловое ускорение. Чем ускорение больше, тем быстрее растет угловая скорость вращения тела гимнаста. Плечо силы достигает своего максимума в горизонтальном положении. В крайних верхнем и нижнем положениях плечо равно нулю. При движении сверху вниз по окружности угловое ускорение соответственно увеличивается, достигает максимума в горизонтальном положении, затем уменьшается до нуля в крайнем нижнем положении. С началом вращательного движения вверх момент силы меняет свой знак на противоположный. Отрицательное ускорение растет по своей абсолютной величине, достигая максимума в горизонтальном положении – вращение тормозится. В соответствии с этим при движении сверху вниз скорость вращения все время растет и становится максимальной в крайнем нижнем положении, а при движении снизу вверх она все время уменьшается. Быстрее всего скорость изменяется в момент прохождения горизонтального положения, когда возникает ее максимальный (по абсолютной величине) прирост. В крайних нижнем и верхнем положениях он равен нулю. Если пренебречь силой трения и сопротивлением воздуха, то тело в этом случае выполнит полный оборот и скорость его вращения при возвращении в исходное положение будет равна исходной. Если не пренебрегать силой трения рук гимнаста о перекладину, то при совершении вращательного движения без изменения позы он снова в вертикальное положение не выйдет. Рассмотрим, каким образом то или иное изменение позы отразится на характере вращательного движения (Курысь В.Н., 1994). Согласно формуле (5.12) своего максимального значения [d] достигает при горизонтальной ориентации тела в полностью выпрямленной позе с максимальной «оттяжкой» от опоры. В этой позе будет наибольший момент силы тяжести и, следовательно, наибольшее угловое ускорение при данной ориентации. Чем больше момент силы тяжести и чем дольше он действует, тем больше будет кинетический момент относительно оси вращения. Общее сгибание или прогибание тела за счет соответствующих движений в суставах (включая межпозвоночные) уменьшит величину [d] и соответственно [M] и [ε]. Поэтому при движении сверху вниз гимнасту выгодно сохранять полностью выпрямленную, вытянутую в линию осанку. При движении снизу вверх общее сгибание или прогибание тела приблизит ОЦТ гимнаста к оси вращения. В результате уменьшится абсолютная величина отрицательного момента силы тяжести, тормозящего вращение, за счет воздействия на гимнаста положительного момента сил Кориолиса. Приближение ОЦТ тела к перекладине, а значит, уменьшение момента инерции тела, ускоряет вращение гимнаста, а удаление замедляет его, что и следует из закона сохранения кинетического момента при условии пренебрежения силами трения между перекладиной и кистями рук спортсмена. Таким образом, изменяя позу и радиус инерции, гимнаст может управлять скоростью вращения тела вокруг опорной оси. При этом одинаковые движения, выполняемые в разных суставах, дают различный эффект. При прочих равных условиях движения в суставах, близких к оси вращения, наиболее эффективны. Например, сгибание на один и тот же угол в лучезапястных суставах (без прокручивания кистей) будет более эффективным, чем в плечевых, а в плечевых – более эффективным, чем в тазобедренных. Однако здесь следует учитывать целый ряд факторов: угловую скорость суставных движений; силовые возможности мышц для развития суставных моментов, требуемых для выполнения движения в конкретных суставах; фактор упругой опоры; действие центробежной силы инерции на связи. Один и тот же механический эффект при выполнении упражнений большим махом может быть получен за счет движения как в плечевых, так и в тазобедренных суставах. Во втором случае для этого требуется большая амплитуда движения, поэтому поза гимнаста изменится более заметно. Чем больше скорость движения в обоих случаях, тем больше эффект. Если же оба движения выполнить совместно, добавив к ним движение в межпозвоночных суставах, то суммарный эффект соответственно возрастет. Поэтому основное рабочее действие практически никогда не локализуется в каком-то одном суставе. Начинаясь с дистальных звеньев, оно всегда носит общий характер и осуществляется путем согласованного сокращения почти всех мышц той или иной поверхности тела. При вращении гимнаста в направлении сверху вниз сила тяжести его тела совершает положительную работу, при движении снизу вверх сила тяжести совершает уже отрицательную работу, замедляя движение. Кроме того, в реальном вращательном движении сила трения между перекладиной и руками гимнаста рассеивает часть кинетической энергии вращательного движения. Для выполнения гимнастом упражнений необходимо, чтобы положительная работа была больше отрицательной и компенсировала необратимые потери энергии. Для этого спортсмен уменьшает отрицательную работу за счет уменьшения момента силы тяжести в движении снизу вверх путем уменьшения плеча силы, т.е. притягиваясь к перекладине (Попов Г.И., 2005). 4.2. Основные способы управления движениями вокруг осей |
