КП_Тишинский. 5. Решение задачи линейного программирования вручную 10
 Скачать 5.67 Mb.
|
Метод искусственного базиса решения задач линейного программированияСимплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме. М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М - достаточно большое положительное число. В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные. В процессе решения М-задачи Искусственные векторы выходят из базиса, в результате чего будет получен опорный план. В противном случае исходная задача неразрешима.
При откорме, каждое животное должно получить не менее 9 ед. белка, 8 ед. протеина, и 10 ед. углеводов. Для составления рациона используется 2 вида корма, состав которых приведён в таблице. Стоимость 1 кг. Первого составляет 4 ден. ед., а второго 6 ден. ед.. Составьте дневной рацион питательности, имеющий минимальную стоимость. Таблица 2 Состав питательных веществ в кормах
Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многообразны и сложны, что лучшим способом изучения часто является построение модели, отражающей лишь какую-то часть реальности. В любом случае модель строится с целью узнать про объект что-либо новое или сохранить об объекте информацию, которая может стать недоступной в будущем. Как правило, процесс изучения, связанный с использованием моделей и называемый моделированием не заканчивается созданием одной модели. Построив модель и получив с её помощью, какие-либо результаты, соотносят их с реальностью, и если это соотношение даёт неудовлетворительные результаты, то в построенную модель вносят коррективы или даже создают другую модель. В случае достижения хорошего соответствия с реальностью выясняют границы применения модели. Это очень важный вопрос, он решается путём сравнения модели с оригиналом путём сравнения предсказаний, полученных с помощью компьютерной модели. Если это сравнение даёт удовлетворительные результаты, то модель принимают на вооружение, если нет, приходится создавать другую модель. Математическое моделирование относится к классу знакового моделирования, при этом модели могут создаваться из любых математических объектов, чисел, функций, уравнений, графиков, графов. Практически во всех науках построение и использование моделей является мощным орудием познания. Цель задачи заключается в нахождение рациона питания, который бы восполнял минимальный набор питательных веществ. При минимальных денежных затратах. Пусть  число килограммов корма 1-го вида, а  число килограмм корма 2-го вида необходимых для составления рациона.Цель задачи: Минимизировать расход, при соблюдение нормы рациона. Следовательно,  Состав питательных веществ в рационе не должен быть меньше необходимой дневной нормы. Отсюда следует система неравенств: 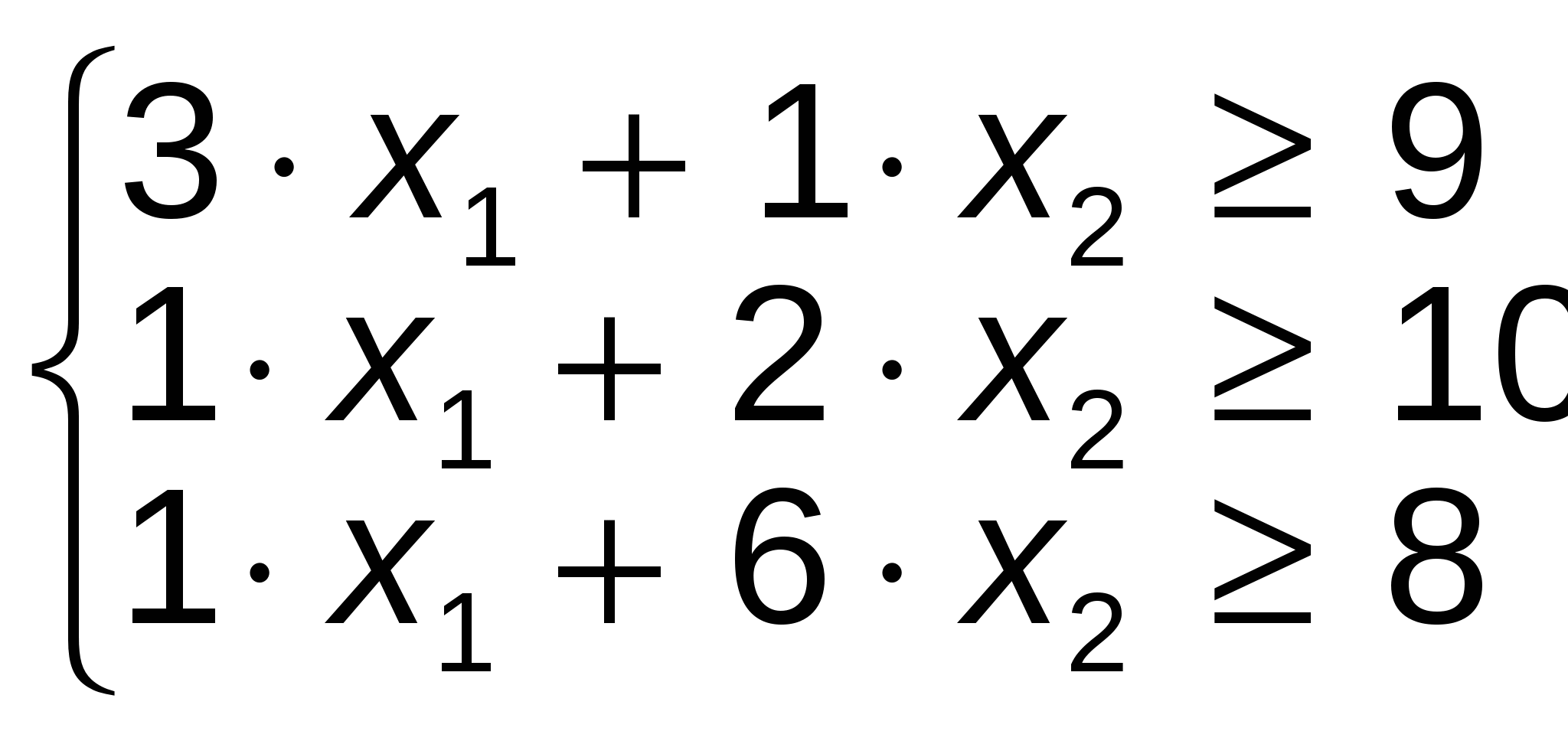 | ||||||||||||||