Решение простейших однокритериальных задач. Сведение произвольной задачи линейного программирования к основной задаче линейного. Практическая работа 1 Решение простейших однокритериальных задач. Сведение произвольной задачи линейного программирования к основной задаче линейного программирования, решение задач линейного программирования различными методами Цель работы

• Название: Практическая работа 1 Решение простейших однокритериальных задач. Сведение произвольной задачи линейного программирования к основной задаче линейного программирования, решение задач линейного программирования различными методами Цель работы
• Анкор: Решение простейших однокритериальных задач. Сведение произвольной задачи линейного программирования к основной задаче линейного
• Дата: 29.09.2022
• Размер: 338.24 Kb.
• Имя файла: п1.docx
• Тип: Практическая работа; #704951

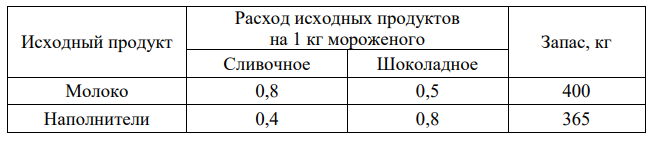
Практическая работа №1

Решение простейших однокритериальных задач. Сведение произвольной задачи линейного программирования к основной задаче линейного программирования, решение задач линейного программирования различными методами

Цель работы: приобрести умения сведения произвольной задачи к задачи линейного программирования, решения задач линейного программирования различными методами.

Оборудование: Ms Excel, выход в Интернет

Источники:

1. 
   Графический метод решения задач линейного программирования. https://youtu.be/FCMjnTuxKGA
   
2. 
   Симплекс-метод. https://youtu.be/FCMjnTuxKGA
   
3. 
   Использование инструмента Excel «Поиск решения» для решения задач однокритериальных задач. https://youtu.be/tFnEvcm3EAQ
   
4. 
   Презентация к уроку «Понятие решения. Множество решений, оптимальное решение. Показатель эффективности решения. Общий вид и основная задача линейного программирования. Симплекс – метод»
   

ТРЕБОВАНИЯ К СОДЕРЖАНИЮ ОТЧЕТА ПО ПРАКТИЧЕСКОЙ РАБОТЕ:

Отчет должен содержать:

1. 
   Номер, название, цель практической работы, использованное оборудование и/или программное обеспечение
   
2. 
   Условие задач, решение задач, ответ
   
3. 
   Выводы по практической работе
   

ЗАДАНИЯ К ПРАКТИЧЕСКОЙ РАБОТЕ

1. 
   Внимательно изучите принцип решения задач графическим методом, симплекс-методом и с использованием инструментов Excel.
   
2. 
   Сведите предложенную экономическую задачу к основной задаче линейного программирования. (постройте математическую модель согласно выданного преподавателем варианта).
   

Варианты заданий

1	Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида - 10 м, третьего вида - 16 м. Выпуск одного изделия типа А приносит доход 400 д.ед., одного изделия типа В - 300 д.ед. Составьте план производства, обеспечивающий фирме наибольший доход.
2	Для производства двух видов кормовых биодобавок можно использовать витамины трех групп. При этом на изготовление биодобавки «Телец» расходуется 16 кг витамина А, 8 кг витамина В1 и 5 кг витамина Е. На изготовление биодобавки «Овен» расходуется 4 кг витамина А, 7 кг витамина В1 и 9 кг витамина Е. На складе фирмы имеется всего 784 кг витамина А, 552 кг витамина В1 и 567 кг витамина Е. От реализации добавки «Телец» фирма имеет прибыль 4 тыс. руб., а от добавки «Овен» — 7,2 тыс. руб. Определить максимальную прибыль от реализации обеих биодобавок.
3	Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице: Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного мороженого 14 ден. ед. Требуется определить, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
4	Ремонтный завод «Хоперский» выпускает насосы двух типов: топливные и водяные. В комплектацию этих изделий входят четыре основных вида деталей: корпус, платик, манжета, шестерня. Для изготовления топливного насоса требуется один корпус, четыре платика, четыре манжеты и одна шестерня, для изготовления водяного насоса — 1, 2, 4 и 3 комплектующих деталей, соответственно. 13 От реализации одного топливного насоса завод имеет прибыль 50 руб., а от одного водяного — 200 руб. На складе завода имеется следующий запас комплектующих: корпусов — 6 шт; платиков — 8 шт; манжет — 12 шт; шестерней — 9 шт. Составить план производства, обеспечивающий заводу наибольший доход
5	В 1996 г. ОАО «Прицеп» производит совковые и штыковые лопаты. Для их изготовления требуется листовой металл и древесина. Для изготовления одной совковой лопаты требуется 0,04 листа металла и 0,004 м3 древесины, для изготовления одной штыковой лопаты — 0,02 листа металла и 0,004 м3 древесины. Розничная цена одной совковой лопаты 60 руб., а штыковой — 50 руб. Изучение рынка сбыта показало, что спрос на штыковые лопаты превышает спрос на совковые не более, чем на 3 тыс. штук в месяц. Кроме того, спрос на совковые лопаты не превышает 15 тыс. штук в месяц. Сколько лопат каждого вида должно изготовлять АООТ «Прицеп» в месяц, если оно располагает 300 листами металла и 60 м3 древесины и хочет получить максимальный доход от реализации своей продукции?
6	Фирма выпускает два набора удобрений «Купрум-I» и «Купрум-II». В «Купрум-I» входит 3 кг азотных, 1 кг калийных и 1 кг медных удобрений. В «КупрумII» — 1 кг азотных, 2 кг калийных и 6 кг медных удобрений. После осушения торфяных болот для внесения в почву потребовалось по меньшей мере 9 кг азотных, 8 кг калийных и 12 кг медных удобрений. «Купрум-I» стоит 4 усл. ден. ед., а «Купрум-II» — 6 усл. ден. ед. Какие и сколько наборов удобрений необходимо внести, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

3. 
   Решите задачу графическим методом
   
4. 
   Решите задачу с использованием поиск решения в Excel
   
5. 
   Сравните результаты, сделайте выводы по практической работе.
   

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Дана задача: Для производства компьютерных столов I-го и II-го видов требуются три типа ресурсов: дерево, пластик и трудозатраты. Потребности в ресурсах для производства одного стола каждого вида, запасы ресурсов, а также прибыль от реализации одного стола каждого вида, заданы в следующей таблице: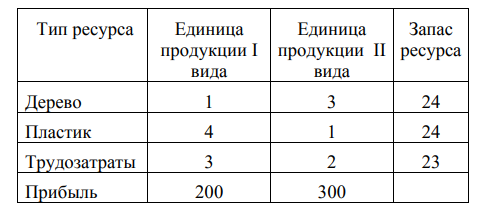



Найти такой оптимальный план производства продукции, который доставляет максимум функции прибыли

Для решения поставленной задачи необходимо:

1. 
   Свести предложенную экономическую задачу к основной задаче линейного программирования
   
2. 
   Решить задачу графическим способом
   
3. 
   Решить задачу с использованием инструмента «Поиск решения» в Excel
   

Решение:

1. 
   Сведем задачу к задаче линейного программирования:
   

Обозначим х – количество выпущенной продукции I вида;

y – количество выпущенной продукции II вида.

Тогда для изготовления х единиц продукции I вида и у единиц продукции II вида нам необходимо (х + 3 у) м ² дерева, но это количество дерева не должно превышать имеющийся запас ресурса, поэтому имеем неравенство (х + 3 у) ≤ 24.

Аналогично делаем выводы по остальным типам ресурсов, т. о. систему ограничений можно записать, используя данные таблицы: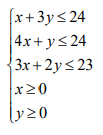



По условию задачи необходимо найти оптимальный план производства продукции, т.е. такой план (х, у), который доставляет максимум функции прибыли. Таким образом, целевая функция F = 200 х + 300 y→max.

Решение задачи графическим способом

2. 
   Найдем область решений задачи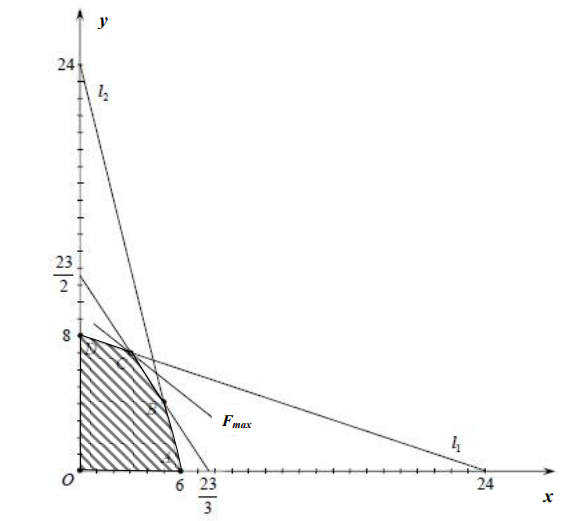
   

Многоугольник ABCDO – область решений системы ограничений.

3. 
   Построим график целевой функции.
   

Для этого рассмотрим вектор N  (2;3) с началом в точке О (0; 0), параллельный вектору (200; 300), нормальному прямой 200 х + 300 y = 0. Построим Fmax y x линию нулевого уровня прибыли F = 0, т.е. прямую 200 х + 300 y = 0. При движении этой прямой в положительном направлении вектора N она пройдет через вершины области решений и станет опорной. В одной из вершин целевая функция примет наименьшее значение, в одной – наибольшее.

4. Найдем оптимальный план задачи.

Для этого найдем координаты вершин пятиугольника: А (6; 0); B(5,4); O(0,0); D(0,8); C = (3;7). Вычислим для точек значение целевой функции:

F(О) = F(0; 0) = 200 · 0 + 300 · 0 = 0;

F(A) = F(6; 0) = 200 · 6 + 300 · 0 = 1200;

F(B) = F(5; 4) = 200 · 5 + 300 · 4 = 2200;

F(C) = F(3; 7) = 200 · 3 + 300 · 7 = 2700;

F(D) = F(8; 0) = 200 · 8 + 300 · 0 = 1600.

Таким образом, наибольшая прибыль достигается в точке C(3; 7), и оптимальный план имеет вид (х, y) = (3; 7).

Ответ. Наибольшая прибыль 2700 рублей достигается при выпуске 3-х компьютерных столов I-го вида и 7 компьютерных столов II-го вида

Решение задачи в Excel с использованием инструмента «Поиск решения»

1. 
   Постройте в Excel таблицу вида (таблица дана с примерами ввода формул):
   

2. После заполнения таблиц формулами, выделить ячейки A3:B3 и вызвать «Поиск решения» [лента Данные]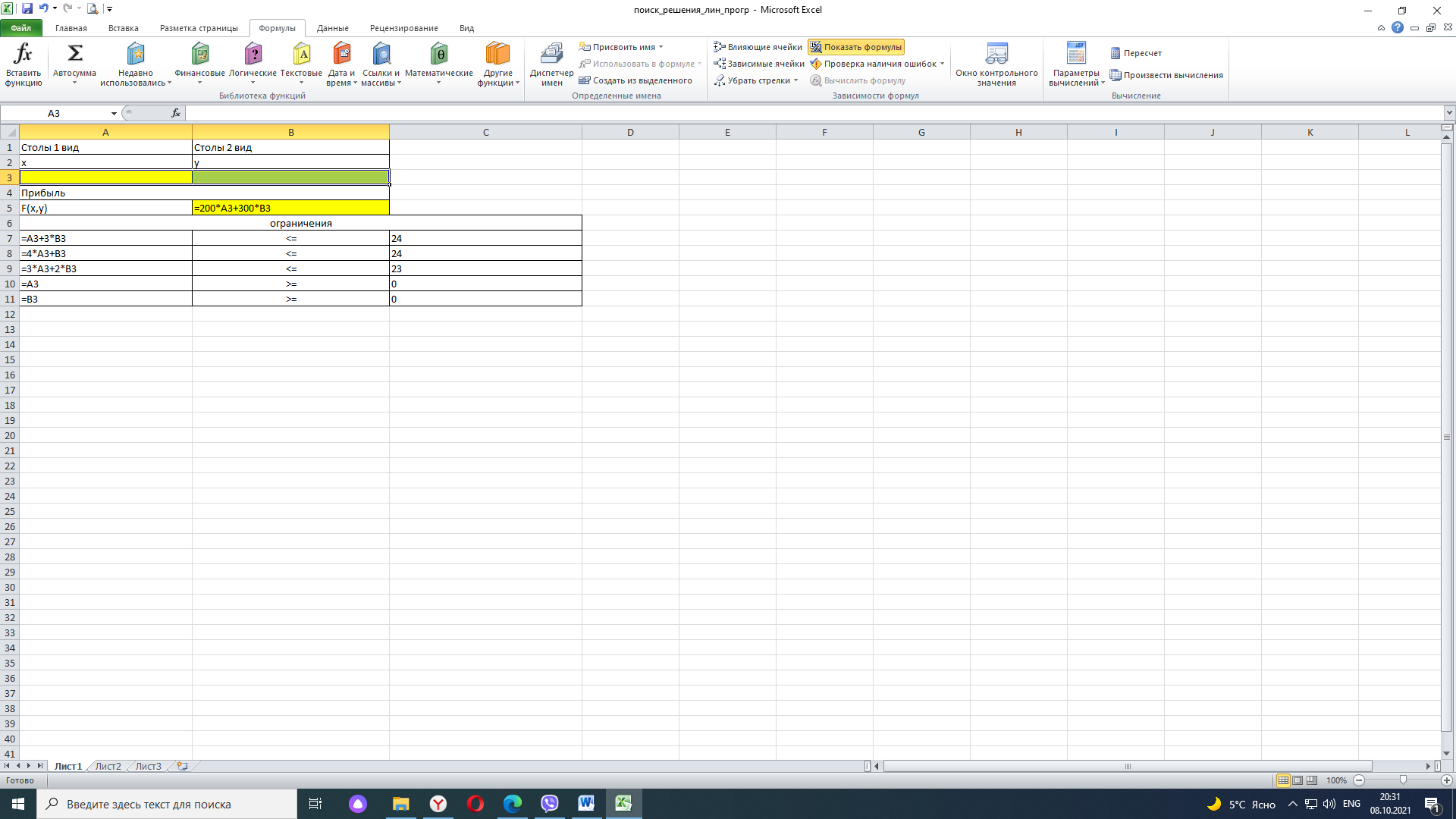

3. 
   Заполнить окно «Поиск решения по образцу»: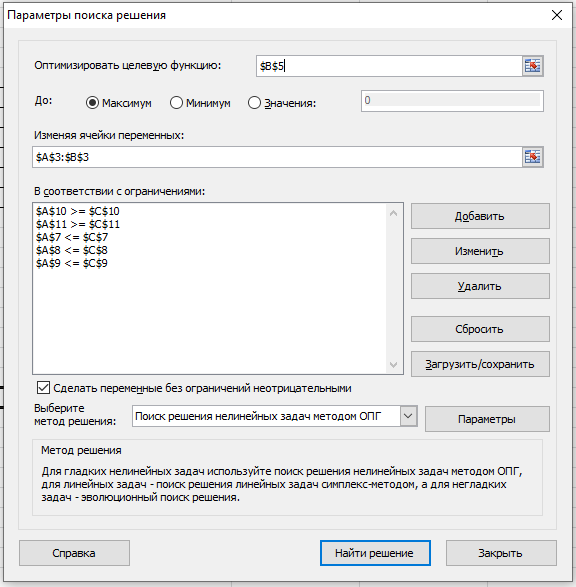
   

3. 
   Оцените полученный результат: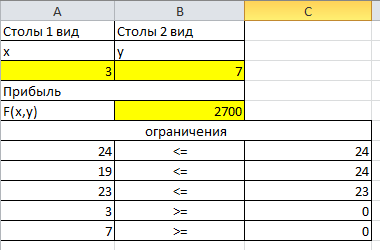
   

Ответ. Наибольшая прибыль 2700 рублей достигается при выпуске 3-х компьютерных столов I-го вида и 7 компьютерных столов II-го вида