моделирование экономических процессов. Матвеева. Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения
 Скачать 272.25 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Моделирование экономических процессов Группа Бк18Э171 Студент Н.Ю. Матвеева МОСКВА2020 Практические занятия№ 1. Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения.Исходные данные представлены в таблице 1. Таблица 1. Линейная оптимизация
Решение: Пусть 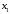 ,  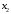,  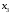– искомые объемы производства продукции. Ограничения имеют вид: Суммарная прибыль от продажи продукции должна быть максимальной:  .Экономико-математическую модель задачи:  Найдем значения переменных  , которые удовлетворяют системе ограничений и дают максимальное значение целевой функции.Для упрощения вычислений умножим систему ограничений на 10. Получим: 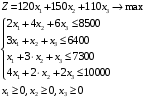 Решим исходную задачу симплексным методам. Приведем модель к каноническому виду: введем дополнительные переменные 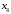 ,  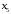,  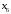, , означающие остатки ресурсов. 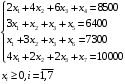Преобразуем целевую функцию – перенесем правую часть влево:  В качестве базисных переменных выбираем 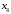, ,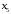 , 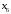. Строим первую симплексную таблицу (начальный опорный план).
Опорный план определяется столбцами базисных переменных и базисных координат): 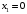 ,  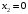,  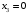, ,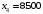 , 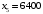 ,  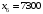.  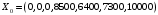. Построенный опорный план X0 не является оптимальным, так как в строке целевой функции есть отрицательные элементы. Необходимо перейти к новому базису и построить новый опорный план. Из всех отрицательных элементов в строке целевой функции выбираем наименьший -150. Столбец, в котором находится этот элемент, называется разрешающим. Вычислим симплексные отношения. Из всех симплексных отношений выбираем наименьшее, и соответствующую строку назовем разрешающей. На пересечении разрешающего столбца и разрешающей строки получаем разрешающий элемент. Получим:
Строим новый опорный план, т. е. составляем новую симплексную таблицу. Переменная, стоящая в разрешающем столбце, переходит в базис (вместо x4 пишем x2). Заполняем столбцы базисных переменных: на месте разрешающего элемента делаем 1, выше и ниже нули, получим:
Данный план не является оптимальным, так как в последней строке есть отрицательный элемент, строим новый опорный план.
Строим новый опорный план, т. е. составляем новую симплексную таблицу. Переменная, стоящая в разрешающем столбце, переходит в базис (вместо x5 пишем x1). Заполняем столбцы базисных переменных: на месте разрешающего элемента делаем 1, выше и ниже нули, получим:
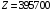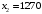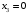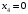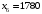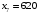Полученный в таблице план является максимальным, так как в последней строке нет отрицательных значений. Максимальное значение функции равно  и достигается оно при  ,  , ,  ,  ,  ,  .Таким образом, следует выпускать 1710 ед. продукта 1 и 1270 единиц продукта 2, при этом прибыль будет максимальной и составит 395700 ден. ед. Ответ: предприятие может выпускать 1710 ед. продукта 1 и 1270 ед. продукта 2, при этом прибыль будет максимальной и составит 395700 ден. ед. № 2. Распределить план перевозок однотипного груза от трёх поставщиков к четырём потребителям, обеспечив минимальные затраты на перевозку.Исходные данные представлены в таблице 2. Таблица 2. Транспортная задача.
Решение: Проверим сбалансированность задачи: Общее число запасов 400+550+300=1250, Общая потребность 450+250+200+350=2500. Задача является сбалансированной. Построим оптимальный план методом минимального элемента. Получим:
Минимальный элемент находится в клетке (2;1). Ее загружаем min(550;450)=450. Минимальный элемент находится в клетке (1;4). Ее загружаем min(400;350)=350. Минимальный элемент находится в клетке (1;2). Ее загружаемmin(400-350;250)=min(50;250)=50. Минимальный элемент находится в клетке (3;3). Ее загружаем min(300;200)=200. Минимальный элемент находится в клетке (3;2). Ее загружаем min(300-200;250-50)=min(100;200)=100. Минимальный элемент находится в клетке (2;2). Ее загружаемmin(550-450;250-50-100)=min(100;100)=100. Проверим опорный план на невырожденность. Количество заполненных клеток равно 6, должно быть: n+m–1=4+3–1=6, значит план невырожденный. Общие затраты равны: 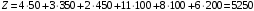 .Проверим оптимальность плана методом потенциалов. Пусть 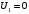 , тогда для занятых клеток имеем  . 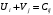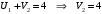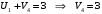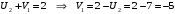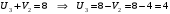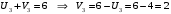, , , , , .Вычислим оценки для незанятых клеток: 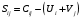 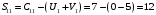 , ,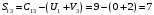 , ,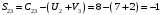 , 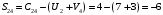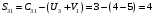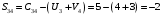.Так как есть оценка 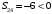 , то план не оптимален. Для клетки (2;4) строим цикл.Помечаем эту клетку знаком «+». Получим:
Перемещать по циклу будем min( 350;100)=100 единиц. В клетке со знаком «+» прибавляем 100 единиц, со знаком «−», вычитаем 100 единиц. Получим новый опорный план:
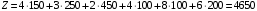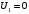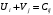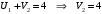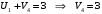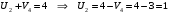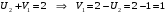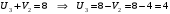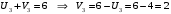Значение целевой функции:  Задача является невырожденной, так как занятых клеток 6. Проверим оптимальность методом потенциалов. Пусть , тогда для занятых клеток имеем . , , , , , .Вычислим оценки для незанятых клеток: 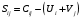 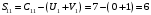, ,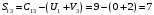 , ,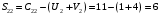 , 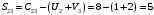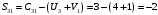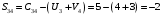.Так как есть оценка 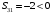 , то план не оптимален. Для клетки (3;1) строим цикл.Помечаем эту клетку знаком «+». Получим:
Перемещать по циклу будем min( 450;250;100)=100 единиц. В клетке со знаком «+» прибавляем 100 единиц, со знаком «−», вычитаем 100 единиц. Получим новый опорный план:
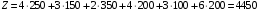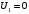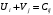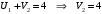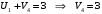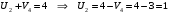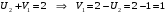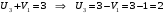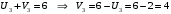Значение целевой функции:  Задача является невырожденной, так как занятых клеток 6. Проверим оптимальность методом потенциалов. Пусть , тогда для занятых клеток имеем . , , , , ,  .Вычислим оценки для незанятых клеток: 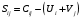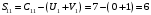, , , ,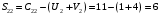 , 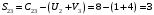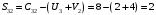.Так как все оценка  , то план оптимален.Ответ: 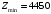 Распределение ресурсов:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
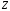
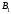
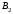
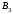
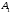
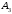
4