Лабораторная работа 1 Решить задачу линейного программирования графическим способом

• Название: Лабораторная работа 1 Решить задачу линейного программирования графическим способом
• Дата: 12.01.2022
• Размер: 201.26 Kb.
• Имя файла: LR1_Metody_optimizatsii_Mukhametyanova_N_PI-312z.docx
• Тип: Лабораторная работа; #329004

ФГБОУ ВО

Уфимский Государственный Авиационный Технический Университет

Кафедра АСУ

Отчет по лабораторной работе №1 по дисциплине

«Методы оптимизации»

Вариант: 33
Выполнила:

ст. гр. ПИ-312з

Мухаметьянова Н.А.
Проверила:

Кондратьева О.

Уфа 2021

Лабораторная работа №1

Решить задачу линейного программирования графическим способом

Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается А1кг сырья первого вида, А2кг сырья второго вида и А3кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается Б1кг сырья первого вида, Б2кг сырья второго вида и Б3 кг сырья третьего вида. Запасы сырья первого вида составляют Запасы1 кг, второго – Запасы2 кг, третьего – Запасы3 кг. Прибыль от реализации единицы продукции первого вида составляет С1 ден.ед., прибыль от реализации единицы продукции второго вида составляет С2 ден.ед. Определить оптимальный план выпуска продукции, чтобы прибыль от реализации была максимальной.

Сырье	Расход сырья на ед. продукции		Запасы сырья
	П1	П2
А1/B1	6	3	230
A2/B2	9	12	210
A3/B3	10	8	250
Прибыль	18	20	690

Ход работы:

1. 
   Идентифицируем переменные задачи:
   

Обозначим х1 – количество продукции П1 и х2 – количество продукции П2, которые нужно производить предприятию.

2. 
   Производство продукции ограничено запасами сырья А1, А2, А3, В1, В2, В3. Также учтем, что количество производства не может быть отрицательным. Запишем ограничения по ресурсам математически: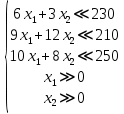
   

3. 
   Цель задачи состоит в получении максимальной прибыли, поэтому целевая функция будет выглядеть: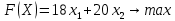
   

4. 
   Получим пять уравнений прямых, заменив знак неравенства на равенство: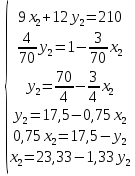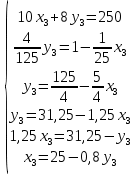
   

5. 
   
   

5. Построим эти прямые на координатной плоскости:



6. Найдем полуплоскости, определяемые каждым из ограничений задачи в соответствии со знаком неравенства:



7. Найдем область допустимых решений, т.е. многоугольник решений и заштрихуем его.



8. Построим направляющий вектор по двум точкам – (0;0) и (18;20) и найдем точку оптимума, для этого построим прямую через начало координат и перпендикулярно вектору , будем передвигать эту прямую параллельно самой себе в направлениях вектора (вверх и вправо) до тех пор, пока прямая не коснется крайней точки многоугольника решений, то есть точки R.



9. Найдем координаты точки R. Решим систему уравнений:







Ответ: предприятию необходимо производить 23,33 ед. продукции вида П1 и 0 ед. продукции вида П2, при этом прибыль от реализации будет максимальной и равна 420 ден.ед.