Графическое решение уравнений и систем уравнений в Excel

• Название: Графическое решение уравнений и систем уравнений в Excel
• Дата: 18.12.2021
• Размер: 274.09 Kb.
• Имя файла: Laboratornaya_12.docx
• Тип: Отчет; #308332

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС


отчет

по лабораторной работе №12

по дисциплине «Информатика»

Тема: Графическое решение уравнений и систем уравнений в Excel

Студент гр. 1408		Матвейцов А.Е.
Преподаватель		Пожидаев А.К.

Санкт-Петербург

2021

Цель работы: ознакомиться с графическими методами решения уравнений и систем уравнений.

Ход работы:

Задание 1. Решить графически уравнение y = cos²(pi*x) на интервале [0; 1].
1. Открыл Excel;

2. Составил таблицу значений переменных для уравнения. Значения переменной «x» взяты на интервале x∈[0; 1] с шагом Δх = 0,1. Значения переменной «y» вычислил при помощи формулы (=COS(A3*С$3)^2).

4. В решение потребуется значение числа «π». Ввёл его значение как «3,1415».

5. Получил таблицу: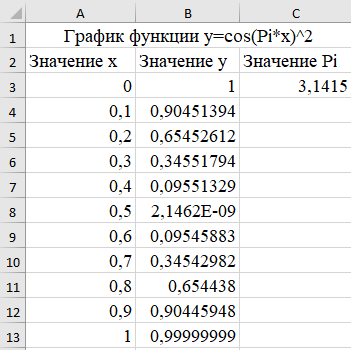


6. С помощью данной таблицы построил график функции: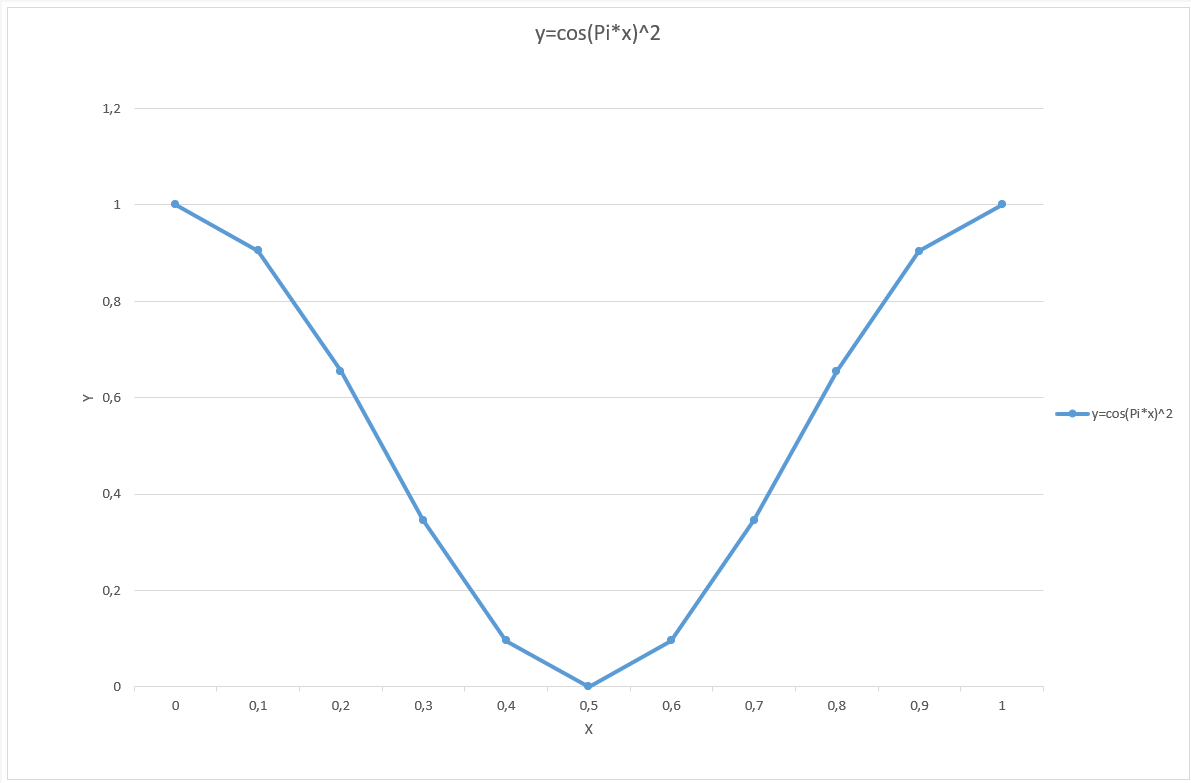



Задание 2. Решить графически уравнение х³ – 4х² – 3х + 6 = 0.

1. Изменил вид данного уравнения, тем самым выполнив построение двух графиков, пересечения которых будут являться решением уравнения;

2. Аналогично первому задания построил таблицу, при помощи которой можно графически решить уравнения. Кубическое уравнение будет иметь 3 корня. Для поиска этих корней нужно выбрать подходящий интервал значений переменной «x». Значение переменной «x» взято на интервале x∈[-2; 4,8] с шагом Δх=0,4, а значения для первого (y₁=x³) и второго (y₂=4x²+3x-6) графика вычислил при помощи соответствующих формул (=A3^3 и 4*A3^2+3*A3-6 соответственно).

3. В итоге получил таблицу: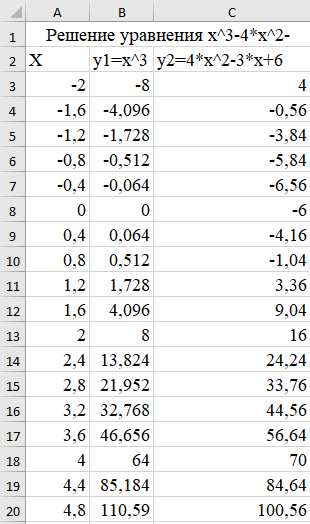



4. С помощью данной таблицы построил график функции: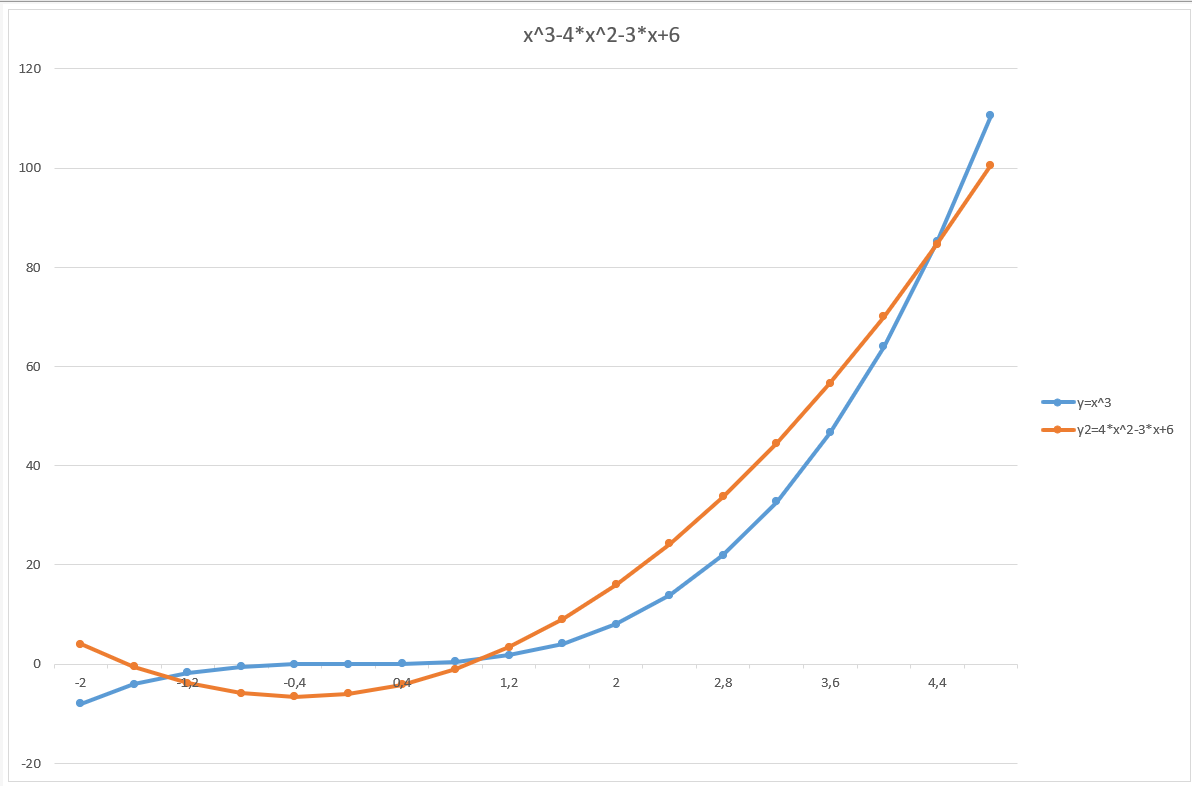



5. Точки пересечения графиков будут являться корнями заданного уравнения (x₁=-1,2; x₂=1,2; x₃=4,4);

Задание 3. Решить графически систему уравнений 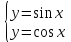в диапазоне х ∈ [0; 3] с шагом Δх = 0,2.

1. Аналогично второму заданию нужно найти пересечения двух графиков функции, т.к. точки пересечения графиков – корни уравнения.

2. Построил таблицу для графического решения системы. Значения переменной взяты в диапазоне x∈[0; 3] с шагом Δх = 0,2. Значения первого (y₁=sin(x)) и второго (y₂=cos(x)) графиков нашёл с помощью формул (: =SIN(A3) и =COS(A3));

3. Получил таблицу: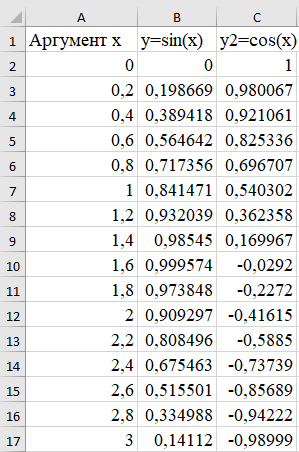



4. С помощью составленной таблицы построил график данной системы: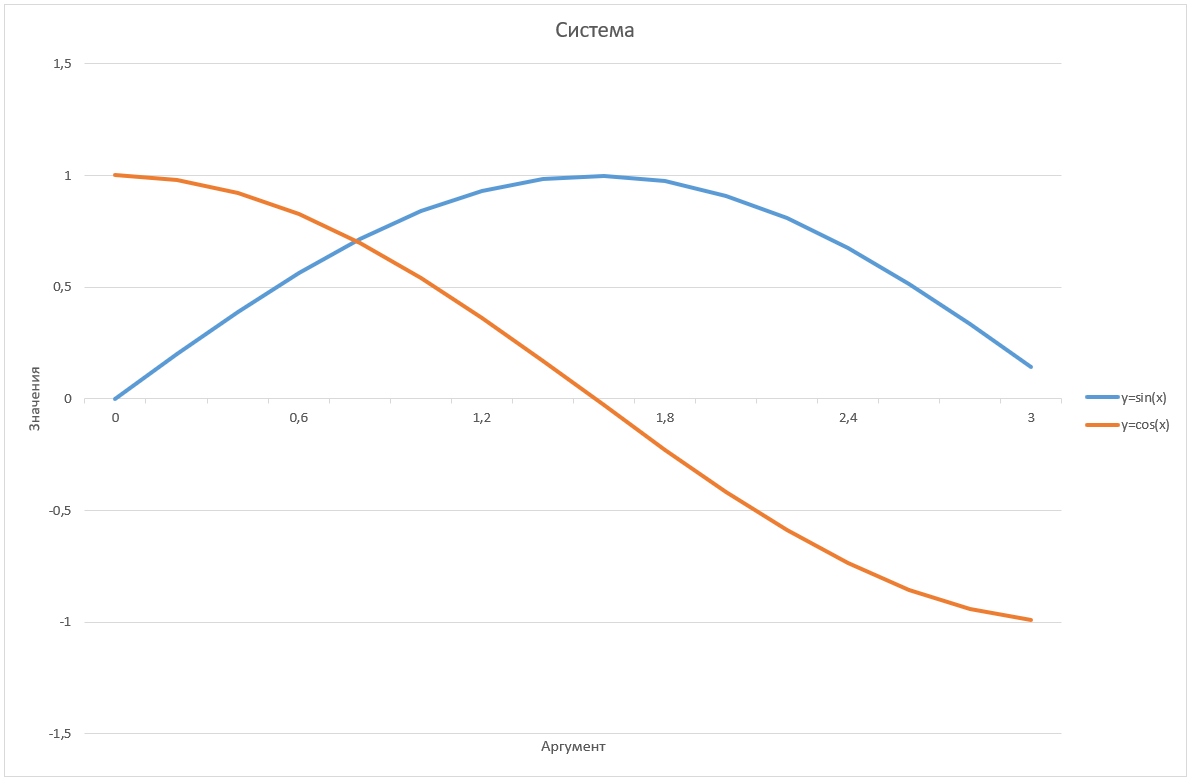



5.Точка пересечения графиков x=0,8; y=0,697 – решение уравнения.

Задание 4. Решить систему уравнений согласно индивидуальному заданию (вариант 5).

20. Аналогично третьему заданию составил таблицу по решению системы уравнений и построил график по данной таблице;

21. Система задана двумя графиками y=cos(x) и y=2x в диапазоне x∈[0,2;3] с шагом Δх=0,1. Значения графиков нашёл с помощью специальных формул ( =СOS(A3) и =2*A3 соответственно);

22. Получил таблицу: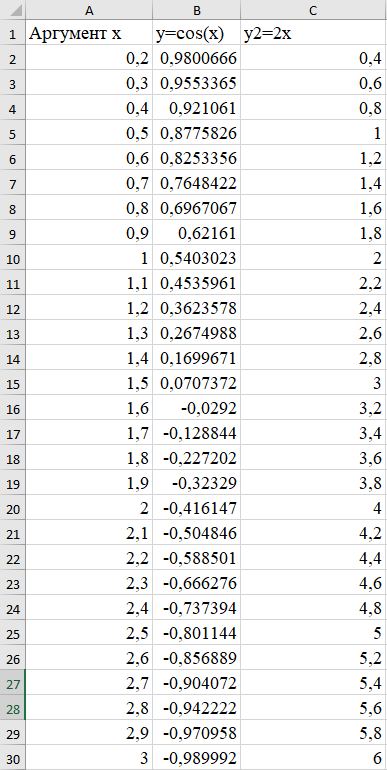



23. По составленной таблице построил графики функций: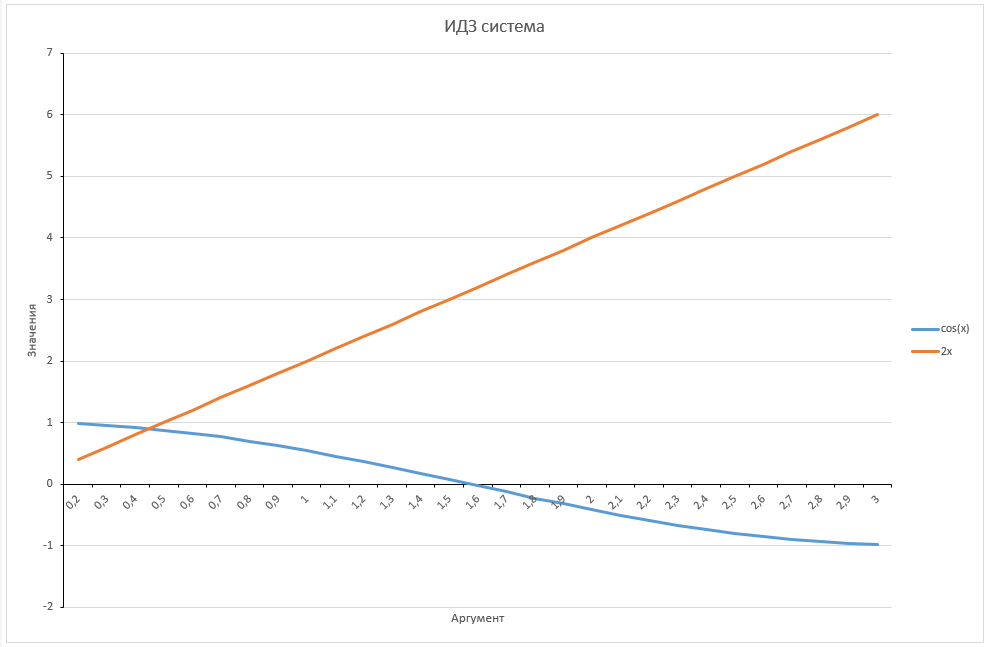



24. Решением системы конкретно в этом диапазоне являются координаты x=0,5 и y=1.

Вывод: в ходе выполнения данной лабораторной работы ознакомился с графическими методами решения уравнений и систем уравнений в программе Excel.