основы геохимии. 5. Вычисление коэффициента остаточной продуктивности
 Скачать 3.83 Mb. Скачать 3.83 Mb.
|
|
Геометризация интенсивности рудообразующего процесса Для оценки интенсивности накопления и перераспределения химических элементов в отдельных точках пространства существует множество различных коэффициентов, наиболее ранним из которых является предложенный Н.И.Сафроновым (1978) показатель энергии рудообразования, отражающий изменение энтропии системы: Е = (ККi* ln(ККi), где ККi – кларк концентрации в пробе элемента i. Этот показатель отражает концентрационную зональность рудообразующей системы, причем фиксирует он не только зоны привноса, но и зоны выноса элементов. Различные модификации коэффициентов аномальности, учитывающих только привнос элементов, обычно сводятся к формуле типа:  , , где КК – кларк концентрации элемента i, m – число элементов с КК>1. Такие показатели обычно используют при анализе вторичных геохимических полей, поскольку применение показателя «энергии рудообразования» в этом случае не вполне корректно. Индивидуальное задание. Вычислить и геометризовать значения показателя энергии рудообразования в плоскости разрезов по линиям скважин 150-96 и 322-50. Оценить положение золоторудных тел в структуре концентрационной зональности аномального геохимического поля. Геометризация значений коэффициентов зональности В основе исследования зональности первичных ореолов лежит представление о различной подвижности элементов в процессе рудоотложения. Ряд вертикальной зональности носит статистический характер, поэтому для конкретных типов оруденения следует опытным путем вычислять этот ряд на эталонных месторождениях и рассчитывать наиболее информативные коэффициенты зональности. Этой процедуре посвящена лабораторная работа № 6. В случаях, когда результатов исследований по эталонным месторождениям нет, можно вычислять коэффициенты зональности на основе общетеоретических представлений. Наиболее широко используются отношения геохимически родственных элементов, подвижность которых в гидротермальных процессах различна, например: Ag/Au, Pb/Zn, Co/Ni. Индивидуальное задание. Вычислить и геометризовать значения показателей Ag/Au, Pb/Zn, Co/Ni в плоскости разрезов по линиям скважин 150-96 и 322-50. Оценить положение золоторудных тел в структуре выявленной зональности аномального геохимического поля. Метод факторного анализа Факторный анализ связан с разделением общей многомерной дисперсии на составные части, каждая из которых связана с воздействием своего фактора. Если полную дисперсию представить в виде многомерного эллипсоида, то длины осей этого эллипсоида отражают силу вклада каждого из факторов в общую дисперсию. 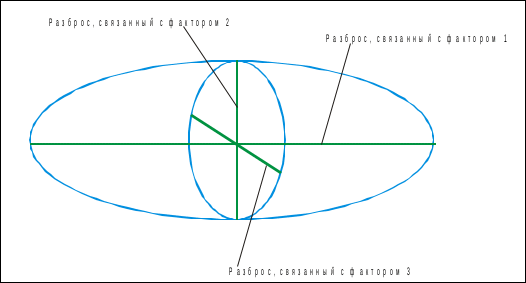 Рис. 1 Геометрическая интерпретация факторного анализа. В категориях матричной алгебры направления главных осей эллипсоида соответствуют собственным векторам корреляционнй матрицы, а длина этих осей соответствует корню из величины собственных значений корреляционной матрицы. Эти величины можно вычислить, следовательно, можно количественно оценить вклад каждого фактора в общую дисперсию и степень влияния каждого фактора на распределение значений конкретной переменной. В программе Statistica результат такого вычисления представляется в виде матрицы факторных нагрузок. В этой матрице отражаются коэффициенты корреляции каждого из факторов с каждой из переменных и показан вклад (в % или долях единицы) каждого из факторов в общую дисперсию. По сути дела, факторный анализ позволяет вычленить из общей корреляционной матрицы новую матрицу корреляций, но не отдельных переменных друг с другом, а групп переменных с общими факторами. Поскольку корреляция означает синхронность поведения переменных, мы получаем таким образом информацию о неких процессах, под воздействием которых группы переменных ведут себя сходным образом. Например, матрица факторных нагрузок выглядит следующим образом: Матрица факторных нагрузок W
Как видим, 1-й фактор значимо влияет на все элементы. Такой фактор обычно называют генеральным. Генеральный фактор отрицательно сказывается на контрастности корреляционной матрицы, обуславливая перекрытие выделяемых групп. "Очистка" связей осуществляется с помощью анализа факторных нагрузок 2-го и 3-го факторов. Дать главным факторам геологическую интерпретацию не всегда возможно, но когда это удается, информативность метода резко возрастает. В частности, в рассмотренном примере со 2-м фактором, очевидно, связано проявление щелочного метасоматоза. Понятно, что геометризация на площади участка значений 2-й главной компоненты позволит в этом случае оконтурить зоны щелочного метасоматоза. Дать интерпретацию 1-му фактору сложнее. Возможно, это влияние расстояния от контакта с гранитоидной интрузией. С 3-м фактором, видимо, связан процесс карбонатизации пород. Окончательную интерпретацию факторам можно дать после геометризации значений факторов на геологической основе. Рассмотрим пример. Выполним факторный анализ по Батуринскому проявлению золота в Томском районе (файл batur_1.xls). Полученная матрица факторных нагрузок позволяет выделить три ассоциации элементов, связанных с процессами формирования аномального геохимического поля: 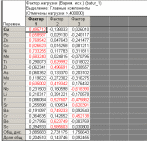 Рис. 2 Матрица факторных нагрузок Батуринского рудопроявления Первый фактор положительно влияет на концентрацию Cu, Pb, Zn, Co, Ni, Mn, то есть способствует их привносу. Поскольку это элементы-спутники золота, входящие в состав сульфидов (Mn входит в состав околорудной карбонатизации), этот фактор можно интерпретеровать как «рудный», то есть как процесс отложения золото-сульфидной минерализации. Второй и третий факторы включают в себя литофильные и сидерофильные элементы, роль которых в оруденении может быть различной, поэтому интерпретацию им дадим после геометризации значений факторов. Значения факторов вычислим, нажав кнопку Значения»:  Рис. 3 Вычисление значений факторов Результаты копируем, вставляем в исходный файл и геометризуем с использованием программы SURFER (файл Батур.srf): 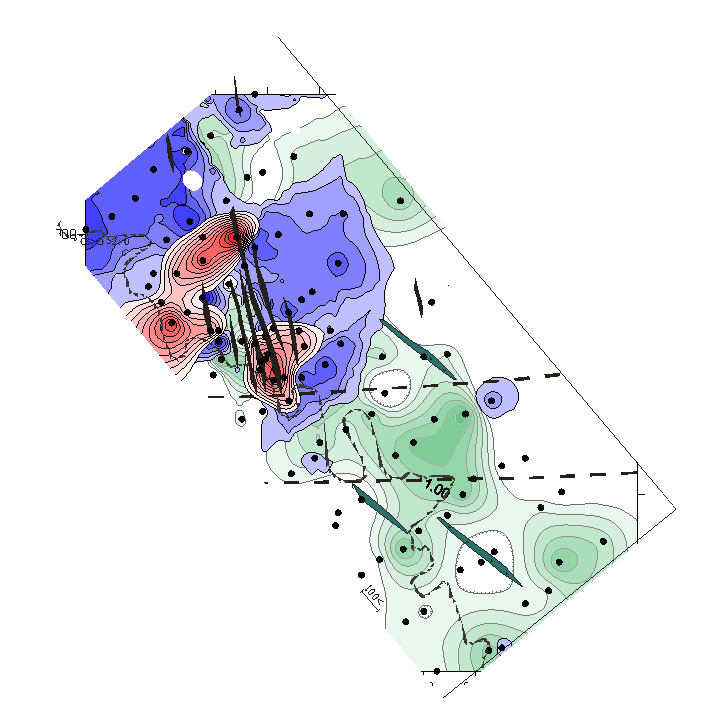 Рис. 4 Распределение аномалий значений факторов на площади рудопроявления Полученная картина показывает, что аномалии фактора 2 окаймляют «рудную» ассоциацию, а повышенными значениями фактора 3 трассируются, видимо, рудоподводящие зоны северо-западного простирания. Входящие в фактор 2 Ti и Zr являются элементами аксессорных минералов, связанных с гранитоидами (ильменит, циркон). Таким образом, подтверждается геофизическая гипотеза о наличии под рудопроявлением, на глубине 1-1,5 км выступа рудогенерирующих гранитоидов: 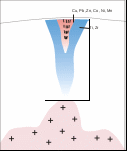 Рис. 5 Гипотетический разрез аномального геохимического поля рудопроявления Батуринского Зоны северо-западного простирания, интерпретируемые как рудоподводящие, пространственно ассоциируются также с пучком даек «томских диабазов». Таким образом, участки сопряжения дайковых пучков с невскрытыми выступами гранитоидов, фикируемые зонально построенными аномальными геохимическими полями, являются благоприятными для поисков золоторудных месторождений в Томском районе. Индивидуальное задание. Провести факторный анализ для разреза по лини скважин 150-63 и 322-50 Синюхинского скарново-золоторудного месторождения (файлы разрез_150_63.xls, разрез_322_50.xls, разрез_150.srf, разрез_322.srf). Дать геологическую интепретацию полученным факторам и оценить возможность использования полученной информации в создании геолого-поисковой модели оруденения. Метод кластер-анализа Кластер-анализ основан на объединении объектов в группы таким образом, чтобы «расстояние» между объектами в группе было минимальным, а между группами – максимальным. В качестве объединяемых объектов могут выступать как переменные, так и наблюдения. Соответственно, при этом выделяются либо ассоциации элементов (минералов), либо ассоциации проб с близкими характеристиками. При обработке геохимических данных, в том и другом случае, исходные многомерные данные должны быть нормированы. Это обусловлено тем, что в кластеры объединяются не только коррелирующиеся между собой элементы, но и те, которые имеют близкий уровень содержаний, то есть, близкие кларки. Нормирование исходных данных можно выполнить по одной из формул: 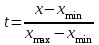 ; ; 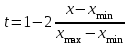 ; ; 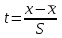 Число кластеров задается исходя из конкретных условий моделирования. Пробы, относящиеся к разным классам, оконтуривают в пространстве области со специфическими геохимическими параметрами. По каждому из выделенных классов рассчитывается геохимический спектр, что позволяет дать их содержательную интерпретацию. Для того, чтобы представлять кластерную структуру исходных данных сначала следует выполнить первый этап – построить дендрограмму:  Далее указать метод объединения в кластеры и метрику «расстояния»:  Полученная дендрограмма наглядно отражает группы родственных элементов и тесноту связи между группами и элементами в группах (расстояние по вертикальной оси):  Ориентируясь на дендрограмму, можно оценить, сколько кластеров следует выделять в последующем анализе. Дальнейший анализ с выделением кластеров, характеристикой их геохимического спектра и геометризацией пространственного распределения кластеров целесообразно проводить для наблюдений (проб), а не для переменных (элементов), поскольку кластер-анализ переменных дает результат, сходный с факторным анализом. Количество кластеров следует задавать больше, чем выделяется групп на дендрограмме, поскольку смесь проб из разных кластеров – это тоже новый кластер. Кроме того, интенсивность проявления конкретных геохимических ассоциаций в результатах кластер-анализа наблюдений напрямую не отражается, но пробы одного класса могут дополнительно разделиться на кластеры с разной интенсивностью процесса накопления элементов. Обычно оптимальным является выделение 8-10 кластеров. Состав кластеров можно оценить, вычислив опцию «Кластерные значения». Кластерам, как и факторам, необходимо дать геологическую интерпретацию. Предварительную – исходя из состава кластеров, окончательную – после геометризации областей распределения кластеров в пространстве. Поскольку интенсивность в результатах анализа не отражается, геометризацию следует производить не в виде изолиний, а в виде точек различного цвета. Каждый цвет соответствует своему кластеру. Принадлежность каждой пробы к определенному кластеру вычисляется в программе и доступна после нажатия кнопки «Сохранить результаты классификации». Индивидуальное задание. Провести кластер-анализ для разреза по линиям скважин 150-96 и 322-50 Синюхинского скарново-золоторудного месторождения (файлы разрез_150_63.xls, разрез_322_50.xls, разрез_150.srf, разрез_322.srf). Дать геологическую интепретацию полученным кластерам и оценить возможность использования полученной информации в создании геолого-поисковой модели оруденения. Общее задание по лабораторной работе № 7 Сформулировать параметры поисковой геохимической модели золотого оруденения синюхинского типа. Поисковая модель должна включать в себя: Вид объемной фигуры (плитообразная, объемная, стержневая); Форма в проекции на дневную поверхность (круглая, овальная, линейная); Положение оруденения в модели. Масштабы развития рудного процесса. Можно выделить три типа моделей по масштабам процесса: а) совокупность мелких изолированных рудопроявлений; б) группа относительно обособленных месторождений среднего масштаба; в) рудные поля с интенсивным развитием рудного процесса, включающие крупные месторождения с хорошо выраженными закономерностями их размещения в единых структурах. Неоднородности геохимического поля. Могут быть связаны как с концентрационной зональностью оруденения (постепенное уменьшение содержаний по мере удаления от руды), так и с сепарационной зональностью (дифференциальная подвижность элементов в гидротермальном процессе). |
