Лекция по авиационной электросвязи. 6. основы оптимального приёма радиосигналов
 Скачать 248.51 Kb. Скачать 248.51 Kb.
|
6. ОСНОВЫ ОПТИМАЛЬНОГО ПРИЁМА РАДИОСИГНАЛОВФункционирование РТС различного назначения, так или иначе, связано с задачей выделения нужных радиосигналов из всего многообразия существующих сигналов в условиях наличия всевозможных помех и воздействия многочисленных дестабилизирующих факторов, приводящих к искажениям передаваемой информации и, соответственно, к ошибкам при принятии решений на основе полученных сведений. Реализация этой задачи наилучшим образом (с минимумом ошибок при принятии решений) называется оптимальным приёмом сигналов. Следует отметить ряд предпосылок при рассмотрении задачи оптимального приёма радиосигналов: вероятностный характер полезных сигналов; случайных характер действия помех (теплового шума); сложность решаемых задач с требуемой достоверностью; применение элементов теории вероятностей и методов математической статистики. Важно учесть и два крайних случая: если о сигнале в месте приёма известно всё, то нет особой необходимости в его приёме; если о сигнале ничего не известно и его не отличить от помех, то приём такого сигнала невозможен. В действительности всегда есть некоторая априорная информация о параметрах сигнала, и поэтому приём сигнала должен увеличивать количество сведений (информации) о нём. Эта добавочная информация после приёма сигнала называется апостериорной. Таким образом, можно говорить о приёме сигналов с полностью или частично известными параметрами. 6.1. Понятие обнаружения радиосигналовС учётом указанных предпосылок и принятых допущений рассмотрим сущность задачи оптимального приёма (обнаружения) сигнала с полностью известными параметрами, которая возникает при приёме сигналов определённой формы в цифровых системах передачи информации, в системах радиолокации при приёме отражённых от объекта эхо-сигналов и предусматривает накопление сигнала и последующее сравнение с некоторым пороговым уровнем l0 (рис. 35). Предположим, что на передающей стороне известны основные параметры полезного сигнала (форма, длительность, период повторения, частота несущего высокочастотного колебания и т.д.). Задача обнаружения заключается в определении наличия полезного сигнала s(t) во входном воздействии y(t), которое при отсутствии сигнала представляет собой шум n(t), а при наличии сигнала – аддитивную смесь, сумму сигнала и шума y(t) = s(t) + n(t). Эта задача решается устройством, которое называется обнаружителем сигнала. Считается, что основные статистические характеристики шума также известны, например, плотность распределения p0(y)значений случайной величины y(t)при наличии на входе обнаружителя только шума n(t) (рис. 35 в). А при аддитивной модели воздействия на входе обнаружителя плотность распределения p1(y)значений случайной величины y(t), в ситуации наличия во входном воздействии полезного сигнала s(t), сместится вверх на величину амплитуды принимаемого полезного сигнала а (рис. 35 г). Сравнивая текущие значения входного воздействия y(t) с некоторым уровнем l0 в пороговом устройстве обнаружителя, выносится решение о наличии или отсутствии в нём полезного сигнала s(t). Однако вследствие случайного характера входного шума, способного как подавить полезный сигнал, так и принять его форму, функционирование обнаружителя может сопровождаться ошибками в принятии решений. 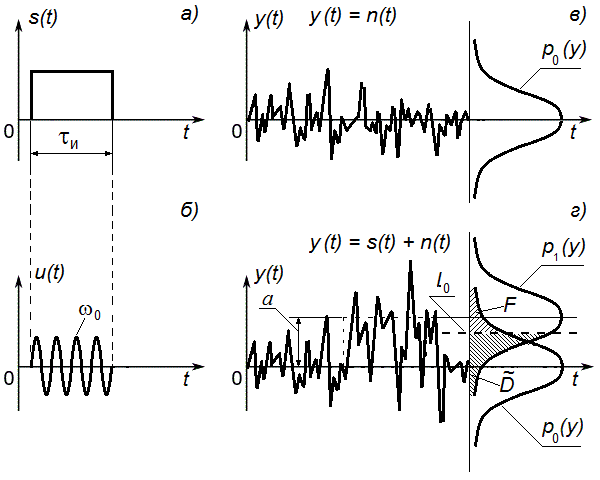 Рис. 35. Обнаружение сигнала с полностью известными параметрами: а) – форма и параметры полезного сигнала, б) – высокочастотное колебание, в) – входное воздействие при отсутствии полезного сигнала, г) – входное воздействие при наличии полезного сигнала В результате анализа принимаемого входного воздействия обнаружитель может принять одно из двух возможных решений: либо полезный сигнал во входном воздействии присутствует, либо он там отсутствует (рис. 36). Таким образом, в работе обнаружителя возможны четыре ситуации, каждая из которых характеризуется соответствующей вероятностью: правильное необнаружение отсутствующего сигнала, 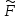 ; ;ошибочное обнаружение несуществующего сигнала («ложная тревога»), F; ошибочное необнаружение сигнала при его наличии («пропуск сигнала»), 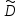 ; ;правильное обнаружение присутствующего сигнала, D. Указанные вероятности связаны между собой следующими соотношениями: 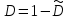 , , 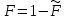 . (6.1) . (6.1)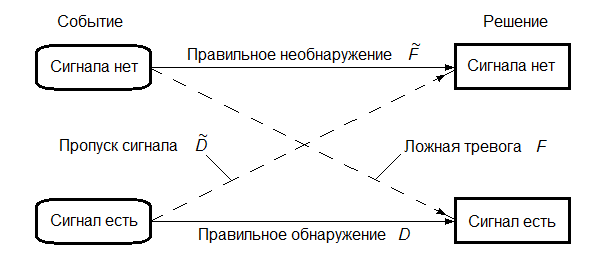 Рис. 36. Возможные ситуации при решении задачи обнаружения Рассмотрим два крайних случая: Вероятность «пропуска сигнала» 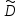 = 0, т.е. обнаружитель всегда будет принимать решение, что во входном воздействии сигнал есть. Тогда вероятность «ложной тревоги» будет максимальна. = 0, т.е. обнаружитель всегда будет принимать решение, что во входном воздействии сигнал есть. Тогда вероятность «ложной тревоги» будет максимальна.Вероятность «ложной тревоги» F = 0, т.е. обнаружитель всегда будет принимать решение, что во входном воздействии сигнала нет. В этом случае вероятность «пропуска сигнала» будет максимальна. Из сравнения этих крайних случаев следует, что требования к ситуациям «пропуска сигнала» и «ложной тревоги» противоречивы, но могут быть оптимизированы. Для этого необходимы некоторые критерии оптимизации. Из всех существующих критериев наиболее широко известны следующие критерии, используемые при решении задачи оптимального приёма (обнаружения) сигналов: минимума среднего риска (Байеса), общий критерий; идеального наблюдателя (Котельникова), применяется в системах передачи информации; Неймана-Пирсона, применяется в радиолокации. Критерий минимума среднего риска (критерий Байеса) предусматривает назначение некоторой стоимости (риска) ошибочным решениям в ситуациях «пропуска сигнала» и «ложной тревоги». Причём риск тем больше, чем опаснее последствия принятия ошибочных решений. При принятии правильных решений какой-либо риск отсутствует совсем, поскольку эти решения отрицательных последствий не имеют. Если назначить риски за принятие ошибочных решений как rпс и rлт, а за правильные решения положить риски равные нулю, то при априорных вероятностях отсутствия P0(y) и наличия P1(y) полезного сигнала во входном воздействии y(t) и случайном характере возникновения ошибочных ситуаций с соответствующими вероятностями «пропуска сигнала» 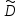 и «ложной тревоги» F, можно записать выражение для среднего риска в виде и «ложной тревоги» F, можно записать выражение для среднего риска в виде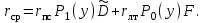 (6.2) (6.2)Оптимизация обнаружения по этому критерию будет заключаться в минимизации величины среднего риска rср подбором порогового уровня l0 (рис. 35, г), с которым производится сравнение входного воздействия y(t) в пороговом устройстве обнаружителя и выносится решение о наличии в нём полезного сигнала в случае превышения уровня l0, или о его отсутствии, когда значения y(t) не превышают этот пороговый уровень. Критерий идеального наблюдателя (критерий Котельникова) является частным случаем критерия Байеса, если назначить одинаковые риски за принятие ошибочных решений, т.е. rпс = rлт = 1. Такая ситуация характерна для систем передачи информации, где оптимизация обнаружения достигается одновременным уменьшением вероятностей «пропуска сигнала» и «ложной тревоги», поскольку в них одинаково нежелательны оба вида ошибочных решений (например, при передаче информации в цифровом виде – переименование символов «0» в «1» и «1» в «0»). Тогда средний риск (6.2) приобретает смысл суммарной вероятности ошибки 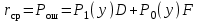 . (6.3) . (6.3)Если учесть, что в цифровых системах передачи информации вероятности появления «0» и «1» в принимаемом сигнале можно считать одинаковыми, т.е P0(y)= P1(y) =0.5, то выражение (6.3) примет вид 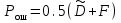 . (6.4) . (6.4)Таким образом, в системах передачи информации оптимизация обнаружения по критерию Котельникова предполагает минимизацию суммы вероятностей «пропуска сигнала» и «ложной тревоги», или, другими словами, минимизацию вероятности ошибки при принятии решения о том, какой символ присутствовал во входном воздействии. Критерий Неймана-Пирсона применяется, в основном, в системах извлечения информации (например, радиолокации), где предъявляются существенно различные требования к двум видам ошибочных решений – «пропуску сигнала» и «ложной тревоге». Ложная тревога является весьма опасным явлением, которое может вызвать крайне нежелательные и даже необратимые последствия, поэтому её вероятность должна быть весьма малой величиной. В радиолокации, например, величина вероятности ложной тревоги задаётся или фиксируется (F = const) на уровне 10-6…10-10, а оптимизация обнаружения по критерию Неймана-Пирсона достигается максимизацией вероятности правильного обнаружения (D → max), или, соответственно, минимизацией вероятности пропуска сигнала, так как D =1 – 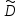 . .Вероятностными характеристиками обнаружения в радиолокации называют зависимость вероятности правильного обнаружения D от соотношения «сигнал/шум» q2 (по мощности) при заданной (фиксированной) вероятности ложной тревоги F, рассчитанные по критерию Неймана-Пирсона. На рис. 37 показаны вероятностные характеристики обнаружения сигналов с различной степенью неопределённости в их параметрах. Сравнение этих характеристик позволяет сделать вывод о том, что чем меньше априорных сведений о сигнале, тем большее отношение сигнала к шуму необходимо обеспечивать при решении задачи обнаружения с требуемой степенью достоверности (вероятностью правильного обнаружения), т.е. потребуются бóльшие затраты энергии в радиопередающем устройстве на излучение более мощного радиосигнала. 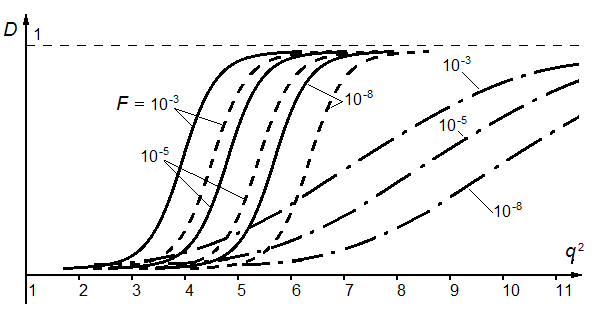 Рис. 37. Вероятностные характеристики обнаружения: ▬▬▬▬ – сигнал с полностью известными параметрами ▬ ▬ ▬ – сигнал с неизвестной и случайной начальной фазой ▬▬ ▪ ▬▬ – сигнал с неизвестной и случайной начальной фазой и амплитудой |
