6. Пирамида это многогранная объемная фигура, ограниченная плоским многоугольником основой
 Скачать 2.75 Mb. Скачать 2.75 Mb.
|
  6. Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания. 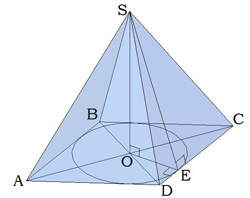 Свойства пирамиды Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга). Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами. Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность. Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр. Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны. 7. П Боковые грани: ABLK, BCML, CDNM, DEPN, EAKP. Основания: ABCDE, KLMNP. ризма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) - параллелограммы, что имеют общие стороны с этими многоугольниками. 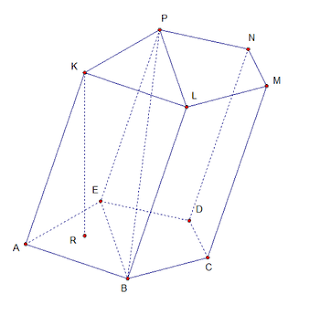 Основные свойства призмы Основы призмы - равные многоугольники. Боковые грани призмы - параллелограммы. Боковые ребра призмы параллельны и равны между собой. Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням. Высота прямой призмы равна длине бокового ребра. Высота наклонной призмы всегда меньше длины ребра. В прямой призме гранями могут быть прямоугольниками или квадратами. 8. Параллелепипедом называется призма, у которой в основании лежит параллелограмм. Все грани параллелепипеда являются параллелограммами. 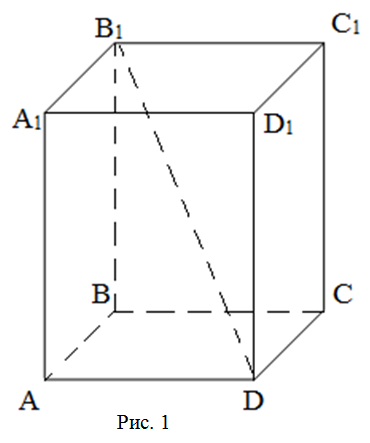 Грани параллелепипеда, не имеющие общего ребра, называются противоположными (АА1В1В и DD1C1C), в противном случае – смежные ( AA1B1B и B1BCC1). Свойства параллелепипеда Все грани параллелепипеда – параллелограммы. Противоположные грани параллелепипеда параллельны и равны. 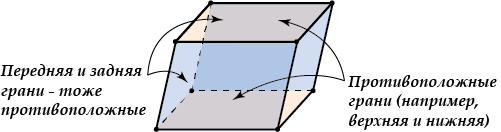 Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные. Боковые ребра параллелепипеда равны: 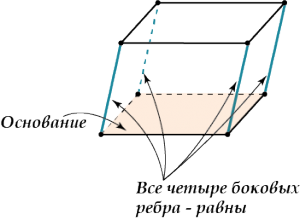 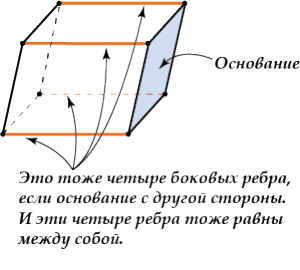 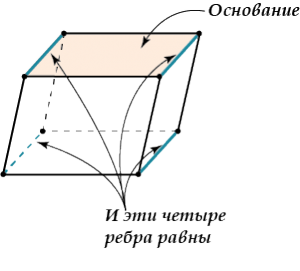 Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам. 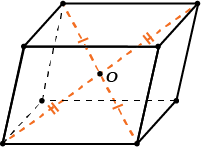 Точка пересечения диагоналей называется центром параллелепипеда. 9. Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра). 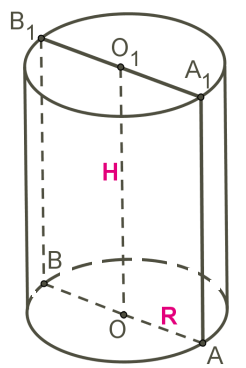 Прямоугольник AOO1A1 вращается вокруг стороны OO1. OO1 — ось симметрии цилиндра и высота цилиндра. AA1 — образующая цилиндра, длина которой равна длине высоты цилиндра. AO — радиус цилиндра. 10. К Треугольник POA вращается вокруг стороны PO. PO — ось конуса и высота конуса. P — вершина конуса. PA — образующая конуса. Круг с центром O — основание конуса. AO — радиус основания конуса. Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось PO конуса. Осевое сечение конуса — это равнобедренный треугольник. APB — осевое сечение конуса. ∡PAO=∡PBO — углы между образующими и основанием конуса. онус — это геометрическое тело, которое образовано совокупностью всех лучей, исходящих из точки и пересекающих любую плоскую поверхность. В месте пересечения образуется основание конуса. 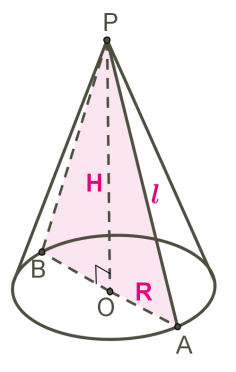 Основные свойства кругового конуса 1. Все образующие прямого кругового конуса равны между собой. 2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус. 3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус. 4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус) 5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3). 6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4). 7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение). 8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы. 11. Ш Основные свойства сферы и шара 1. Все точки сферы одинаково удалены от центра. 2. Любое сечение сферы плоскостью является окружностью. 3. Любое сечение шара плоскостью есть кругом. 4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности. 5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара. 6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара. 7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках. 8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг. ар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой). 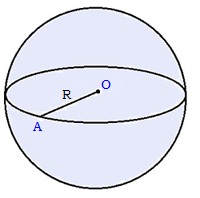       |
