Контрольные задания по лекциям темы 6-8. 6. Ряды динамики

Название	6. Ряды динамики
Дата	28.12.2022
Размер	48.41 Kb.
Формат файла
Имя файла	Контрольные задания по лекциям темы 6-8.docx
Тип	Решение #867809

Тема 6. Ряды динамики

Контрольные задания 6

Вариант 1

Определить абсолютные, относительные и средние показатели ряда динамики цепным и базисным способами, а также произвести непосредственное выделение тренда методом скользящей средней и аналитического выравнивания, используя статистические данные о производстве зерна за несколько лет:

Годы	2006	2007	2008	2009	2010	2011	2012	2013	2014
млн. т	55,5	66,6	65,2	67,2	78,1	78,2	78,6	81,8	83,6

Решение

1. Абсолютные изменения уровней базисным и цепным способами определяются по формулам: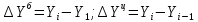

Относительные изменения уровней базисным и цепным способами определяются по формулам: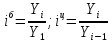

Темпы роста базисным и цепным способами определяются по формулам: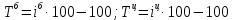

Результаты расчетов показателей представим в таблице.

Годы	Y	∆Y^б	∆Y^ц	i^б	i^ц	Т^б	Т^ц	Ῡ_i	t	t²	Yt	f(t)	(Y – Ῡ)²	(Y –f(t))²
2006	55,5	-	-	-	-	-	-	-	-4	16	-222	59,70	297,75	17,66
2007	66,6	11,1	11,1	1,200	1,200	20	20	62,43	-3	9	-199,8	62,97	37,89	13,21
2008	65,2	9,7	-1,4	1,175	0,979	17,5	-2,1	66,33	-2	4	-130,4	66,23	57,09	1,06
2009	67,2	11,7	2	1,211	1,031	21,1	3,1	70,17	-1	1	-67,2	69,49	30,86	5,25
2010	78,1	22,6	10,9	1,407	1,162	40,7	16,2	74,50	0	0	0	72,76	28,56	28,56
2011	78,2	22,7	0,1	1,409	1,001	40,9	0,1	78,30	1	1	78,2	76,02	29,64	4,76
2012	78,6	23,1	0,4	1,416	1,005	41,6	0,5	79,53	2	4	157,2	79,28	34,16	0,47
2013	81,8	26,3	3,2	1,474	1,041	47,4	4,1	81,33	3	9	245,4	82,55	81,80	0,56
2014	83,6	28,1	1,8	1,506	1,022	50,6	2,2	-	4	16	334,4	85,81	117,60	4,88
Итого:	654,8	-	28,1	-	1,506	-	-	-	0	60	195,8	654,8	715,36	76,40

2. Определим средний уровень ряда динамики по формуле: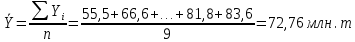

3. Определим среднее абсолютное изменение уровней по формуле: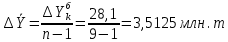

Таким образом, имеет место рост производства зерна в среднем на 3,5125 млн. т в год.

4. Определим среднее относительное изменение уровней по формуле: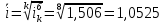

Таким образом, имеет место рост производства зерна в среднем на 5,25% в год.

5. Проведем выделение тренда методом скользящей средней.

Определим трехуровневую скользящую среднюю по формуле: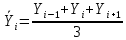

Результаты расчета скользящей средней представлены в таблице.

Фактический ряд динамики и скользящую среднюю представим в виде статистического графика.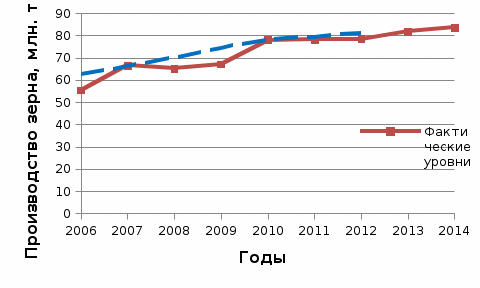

Ряд динамики и линия тренда производства зерна, млн. т

Таким образом, имеет место основная тенденция к увеличению производства зерна в год.

6. Проведем выделение тренда методом аналитического выравнивания.

Определим параметры линейного уравнения тренда по формулам: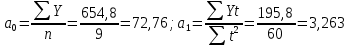

Построим линейное уравнение тренда: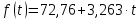

Построим ряд динамики и линию тренда в виде статистического графика.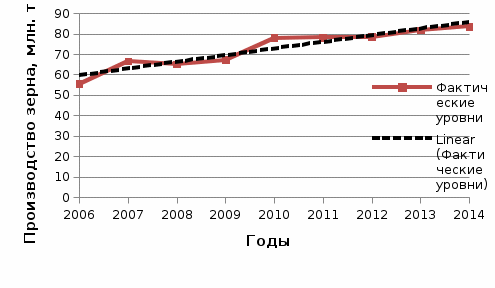

Ряд динамики и линия тренда производства зерна, млн. т

7. Определим расчетное значение критерия Фишера по формуле: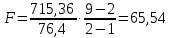

Сравним с табличным значением критерия Фишера 5,59, которое определяем для α = 0,05, а также 1 и 7 степеней свободы. Так как расчетное значение больше табличного, построенное уравнение тренда является надежным.
Тема 7. Индексы

Контрольные задания 7

Вариант 1

Определить индексы и выполнить факторный индексный анализ выручки по следующим данным:

Предприятие	Базисный период		Отчетный период
Предприятие	Количество товара, тыс. ед.	Цена, руб./ед.	Количество товара, тыс. ед.	Цена, руб./ед.
1	180	32	150	35
2	220	51	270	48
3	200	19	240	15

Решение

1. Определим среднюю цену товара в отчетном и базисном периоде по формуле: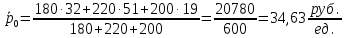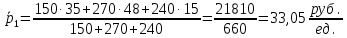

2. Определим выручку от продажи товара каждого предприятия в базисном и отчетном периодах по формуле: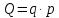

3. Определим долю каждого предприятия в общем количестве товара в базисном и отчетном периодах по формуле: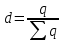

4. Результаты расчетов представим в таблице.

Предприятие	Базисный период				Отчетный период
Предприятие	q₀	p₀	Q₀	d₀	q₁	p₁	Q₁	d₁
1	180	32	5760	0,3	150	35	5250	0,2273
2	220	51	11220	0,3667	270	48	12960	0,4091
3	200	19	3800	0,3333	240	15	3600	0,3636
Итого	600		20780	1	660		21810	1

5. Определим индивидуальные индексы по предприятиям по формулам: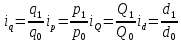

6. Определим общие индексы количества товара, средней цены и общей выручки по формулам: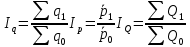

7. Результаты расчетов представим в таблице.

Предприятие	Индексы
Предприятие	q	p	Q	d
1	0,8333	1,09375	0,9115	0,7576
2	1,2273	0,9412	1,1551	1,1157
3	1,2	0,7895	0,9474	1,0909
Итого	1,1	0,9542	1,0496

Таким образом, на предприятии 1 имеет место снижение количества товара на 16,67%, рост цены на 9,375%, снижение выручки на 8,85%, а также доли предприятия на 24,24%. На предприятии 2 имеет место рост количества товара на 22,73%, снижение цены на 5,88%, рост выручки на 15,51%, а также доли предприятия на 11,57%. На предприятии 3 имеет место рост количества товара на 20%, снижение цены на 21,05%, снижение выручки на 5,26%, а также рост доли предприятия на 9,09%.

В целом по трем предприятиям имеет место рост количества товара на 10%, снижение средней цены на 4,58% и рост общей выручки на 4,96%.

8. Определим общий количественный индекс Ласпейреса по формуле: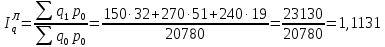

9. Определим общий ценовой индекс Пааше по формуле: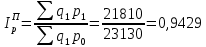

10. Определим общий ценовой индекс Ласпейреса по формуле: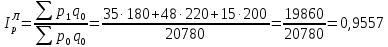

11. Определим общий количественный индекс Пааше по формуле: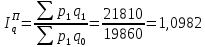

12. Определим общий количественный индекс Фишера по формуле: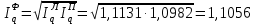

13. Определим общий ценовой индекс Фишера по формуле: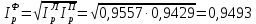

14. Для контроля используем формулу: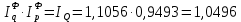

Таким образом, общая выручка увеличилась на 4,96% в связи с увеличением общего количества товара на 10,56% и снижением общего уровня цен на 5,07%.

15. Определим общий индекс выручки по формуле: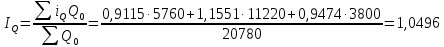

16. Определим общий индекс выручки по формуле: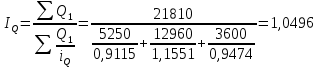

17. Определим индекс переменного состава по формуле: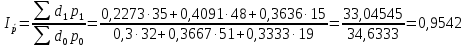

18. Определим индекс структурных сдвигов по формуле: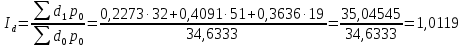

19. Определим индекс постоянного состава по формуле: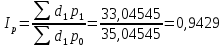

Таким образом, имеет место снижение средней цены товара на 4,58%, в том числе рост на 1,19% за счет структурных сдвигов и снижение на 5,71% за счет динамики цены товара по каждому предприятию.

20. Для контроля используем формулу: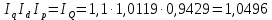

21. Итоговое абсолютное изменение общей выручки: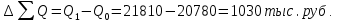

22. Факторные абсолютные изменения общей выручки определим по формулам: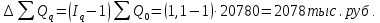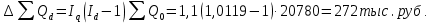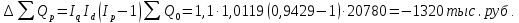

23. Для контроля используем формулу: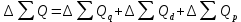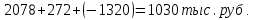

24. Итоговое абсолютное изменение выручки по предприятиям.

предприятие 1: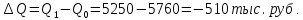

предприятие 2: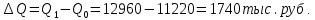

предприятие 3: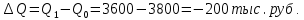

25. Факторные абсолютные изменения выручки по предприятиям.

предприятие 1: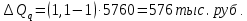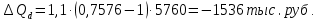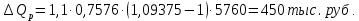

предприятие 2: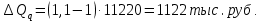

предприятие 3: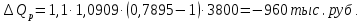

26. Для контроля используем формулу: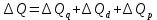

предприятие 1: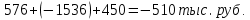

предприятие 2: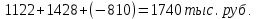

предприятие 3: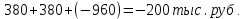

Результаты факторного анализа представлены в таблице.

Предприятие	Абсолютное изменение выручки, тыс. руб.	В том числе по факторам:
Предприятие	Абсолютное изменение выручки, тыс. руб.	количество товара	структура	цена
1	-510	576	-1536	450
2	1740	1122	1428	-810
3	-200	380	380	-960
Итого	1030	2078	272	-1320

Тема 8. Статистическое изучение взаимосвязей

Контрольные задания 8

Вариант 1

1. Определить линейный коэффициент корреляции и построить уравнение регрессии, используя следующие статистические данные по торговым предприятиям:

Товарооборот, млн. руб.	70	100	150	200	300	450	600	800	800	910
Издержки обращения, млн. руб.	10,7	10,9	11,1	11,2	11,9	12,6	13,2	14,0	13,6	14,5

Решение

1. Составим вспомогательную таблицу.

№	X	Y	XY	X²	Y²	Y_X	(Y_X – Ῡ)²	(Y_X – Y)²
1	70	10,7	749	4900	114,49	10,8	2,5604	0,005
2	100	10,9	1090	10000	118,81	10,9	2,1600	0,000
3	150	11,1	1665	22500	123,21	11,1	1,5682	0,000
4	200	11,2	2240	40000	125,44	11,3	1,0709	0,018
5	300	11,9	3570	90000	141,61	11,8	0,3601	0,017
6	450	12,6	5670	202500	158,76	12,4	0,0027	0,032
7	600	13,2	7920	360000	174,24	13,1	0,4962	0,016
8	800	14,0	11200	640000	196	13,9	2,4776	0,003
9	800	13,6	10880	640000	184,96	13,9	2,4776	0,118
10	910	14,5	13195	828100	210,25	14,4	4,2121	0,006
Итого:	4380	123,7	58179	2838000	1547,77		17,3857	0,215

Х – товарооборот, млн. руб. (факторный признак).

Y – издержки обращения, млн. руб. (результативный признак).

2. Определим линейный коэффициент корреляции по формуле: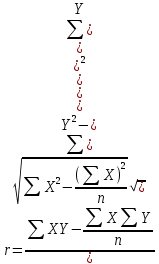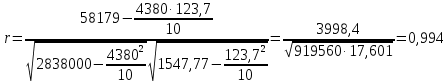

Таким образом, значение коэффициента корреляции свидетельствует о прямой тесной связи между изучаемыми признаками.

3. Определим параметры уравнения парной линейной регрессии по формулам: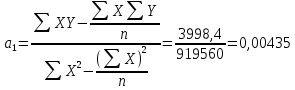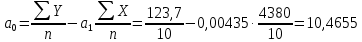

4. Построим уравнение парной линейной регрессии по формуле: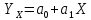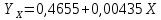

5. Определим теоретические значения регрессии Y_X и занесем в таблицу.

6. Построим фактические значения результативного признака и функцию регрессии в виде статистического графика (эмпирическая и теоретическая линия регрессии).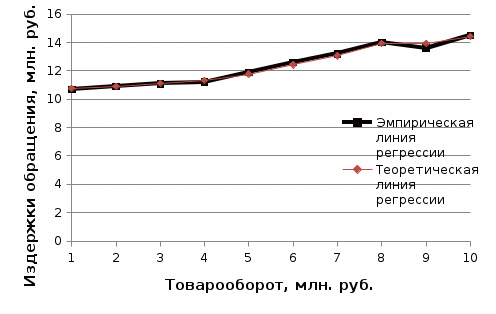

Эмпирическая и теоретическая линия регрессии

7. Определим расчетное значение критерия Стъюдента для линейного коэффициента корреляции по формуле: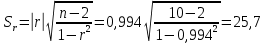

8. Сравним расчетное значение критерия Стъюдента с табличным 2,306, которое определяем для α = 0,05, а также 8 степеней свободы. Так как расчетное значение больше табличного, линейный коэффициент корреляции является значимым параметром взаимосвязи.

9. Определим расчетные значения критерия Стъюдента для каждого из параметров уравнения парной линейной регрессии по формулам: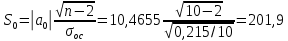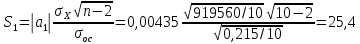

10. Сравним расчетные значения критерия Стъюдента с табличным 2,306, которое определяем также для α = 0,05, а также 8 степеней свободы. Так как расчетные значения больше табличного, то каждый из параметров уравнения парной линейной регрессии является значимым параметром взаимосвязи.

11. Определим расчетное значение критерия Фишера по формуле: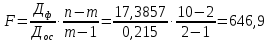

12. Сравним расчетное значение критерия Фишера с табличным 5,32, которое определяем для α = 0,05, а также 1 и 8 степеней свободы. Так как расчетное значение больше табличного, можно сделать вывод о правильности выбора вида взаимосвязи, а также значимости построенного уравнения регрессии.
2. Определить ранговые коэффициенты корреляции по следующим статистическим данным:

Предприятие	Цена спроса на акцию, р./шт.	Цена предложения акции, р./шт.
А	83,6	60,6
Б	83,0	40,7
В	30,3	33,8
Г	13,6	22,1
Д	13,9	33,8
Е	26,5	33,8
Ж	18,1	20,9
З	28,7	35,9
И	19,8	21,7
К	19,0	22,5

Решение

1. Построим единицы совокупности по возрастанию цены спроса на акцию X с соответствующими наименованиями предприятий, а также с присвоением порядковых номеров R_X и R_Y.

Результаты представлены в таблице.

Предприятие	X	Y	Ранги предприятий				Баллы
Предприятие	X	Y	R_X	R_Y	d	d²	Q	P
Г	13,6	22,1	1	3	-2	4	7	2
Д	13,9	33,8	2	6	-4	16	5	3
Ж	18,1	20,9	3	1	2	4	7	0
К	19,0	22,5	4	4	0	0	5	1
И	19,8	21,7	5	2	3	9	5	0
Е	26,5	33,8	6	6	0	0	4	0
З	28,7	35,9	7	8	-1	1	2	1
В	30,3	33,8	8	6	2	4	2	0
Б	83,0	40,7	9	9	0	0	1	0
А	83,6	60,6	10	10	0	0	0	0
Итого			55	55	-	38	38	7

2. Определим расчетные значения d = R_X – R_Y.

3. Определим ранговый коэффициент корреляции Спирмена по формуле: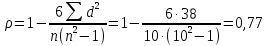

4. Определим расчетные значения баллов Q и P, т.е. случаев, когда ранг признака Y у всех последующих единиц совокупности соответственно больше и меньше, чем у конкретной единицы совокупности.

5. Определим ранговый коэффициент корреляции Кендэла по формуле: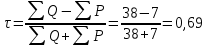

Таким образом, коэффициенты свидетельствуют о прямой тесной связи между изучаемыми признаками.