Задание 1. Задание1 Простейшая обработка данных. Линейная регрессия. Коэффициент корреляции. Его значимость

• Название: Задание1 Простейшая обработка данных. Линейная регрессия. Коэффициент корреляции. Его значимость
• Дата: 25.05.2021
• Размер: 0.74 Mb.
• Имя файла: Задание 1.docx
• Тип: Документы; #209640

Задание№1

Простейшая обработка данных. Линейная регрессия.
Коэффициент корреляции. Его значимость
Цель: научиться находить коэффициент корреляции и определять его значимость; находить коэффициенты регрессии и строить уравнение регрессии.

Основные сведения

Парная регрессия – это уравнение связи двух переменных у и х:

y=f(х),

где у – зависимая переменная (результат, отклик);

х – независимая, объясняющая переменная (фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия: .

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических у_х минимальна.

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и в:



Можно воспользоваться готовыми формулами, которые вытекают из этой системы:



где














Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy для линейной регрессии (—1 <_ r_xy <_ 1):



Теснота линейной связи между переменными может быть оценена на основании шкалы Чеддока:

Теснота связи	Значение коэффициента корреляции при наличии:
	Прямой связи	Обратной связи
Слабая	0,1–0,3	(–0,3)–(–0,1)
Умеренная	0,3–0,5	(–0,5)–(–0,3)
Заметная	0,5–0,7	(–0,7)–(–0,5)
Высокая	0,7–0,9	(–0,9)–(–0,7)
Весьма высокая	0,9–1	(–1)–(–0,9)

Положительное значение коэффициента корреляции говорит о положительной связи между х и у, когда с ростом одной из переменных другая тоже растет. Отрицательное значение коэффициента корреляции означает, с ростом одной из переменных другая убывает, с убыванием одной из переменной другая растет.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 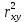, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y , объясняемую регрессией, в общей дисперсии результативного признака.

Соответственно величина характеризует долю дисперсии y , вызванную влиянием остальных, не учтенных в модели, факторов.

Оценку статистической значимости коэффициента корреляции проводят с помощью t-критерия Стьюдента. Выдвигают гипотезу Н₀ о статистически незначимом отличии коэффициента от нуля. Оценка значимости коэффициента корреляции с помощью t-критерия Стьюдента проводится путем сопоставления его значения с величиной случайной ошибки:



Стандартная (случайная) ошибка коэффициента корреляции определяется по формуле:



Сравнивая фактическое и табличное (критическое) значения t-статистики – tтабл и tфакт – принимает или отвергаем гипотезу Н₀.

Если tтабл <tфакт, то гипотеза Н₀ отклоняется, коэффициент корреляции не случайно отличается от. Если tтабл > tфакт , то гипотеза Н₀ не отклоняется и признается случайная природа формирования коэффициента корреляции.
Порядок выполнения работы.

По заданной выборке исследовать зависимость результата у от фактора х. Для этого

2. 
   Создать таблицу данных.
   
3. 
   Найти средние значения 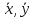, выборочные дисперсии , исправленные средние квадратические отклонения .
   
4. 
   Найти коэффициент корреляции и проверить его значимость.
   
5. 
   Найти коэффициенты линейного уравнения регрессии.
   
6. 
   Построить график прямой регрессии.
   

Пример выполнения задания.

В табл. 1.1 приведены данные об объеме производства у (тыс.ед.) в зависимости от численности занятых х (тыс.чел.) некоторой фирмы.

Таблица 1.1.

Исходные данные

х	11	13	15	18	20	22	24	25	27
у	25	27	31	30	38	43	44	42	49

1. 
   В диапазоне В3:C11 подготовим исходные данные.
   
2. 
   Вводим следующие формулы:
   

Ячейка	Формула	Примечание
D3	=B3*C3	Копируем в диапазон D3:D11
E3	=B3*B3	Копируем в диапазон E3:E11
F3	=C3*C3	Копируем в диапазон F3:F11
B12	=СРЗНАЧ(В3:В11)	Копируем в диапазон В12:F12
А17	=E12-B12*B12	Выборочная средняя фактора
В17	=F12-C12*C12	Выборочная средняя результата
А20	=СТАНДОТКЛОН(B3:B11)	Исправленное среднее квадратическое отклонение фактора
В20	=СТАНДОТКЛОН(C3:C11)	Исправленное среднее квадратическое отклонение результата

Получим следующие результаты (см. рис. 1.1).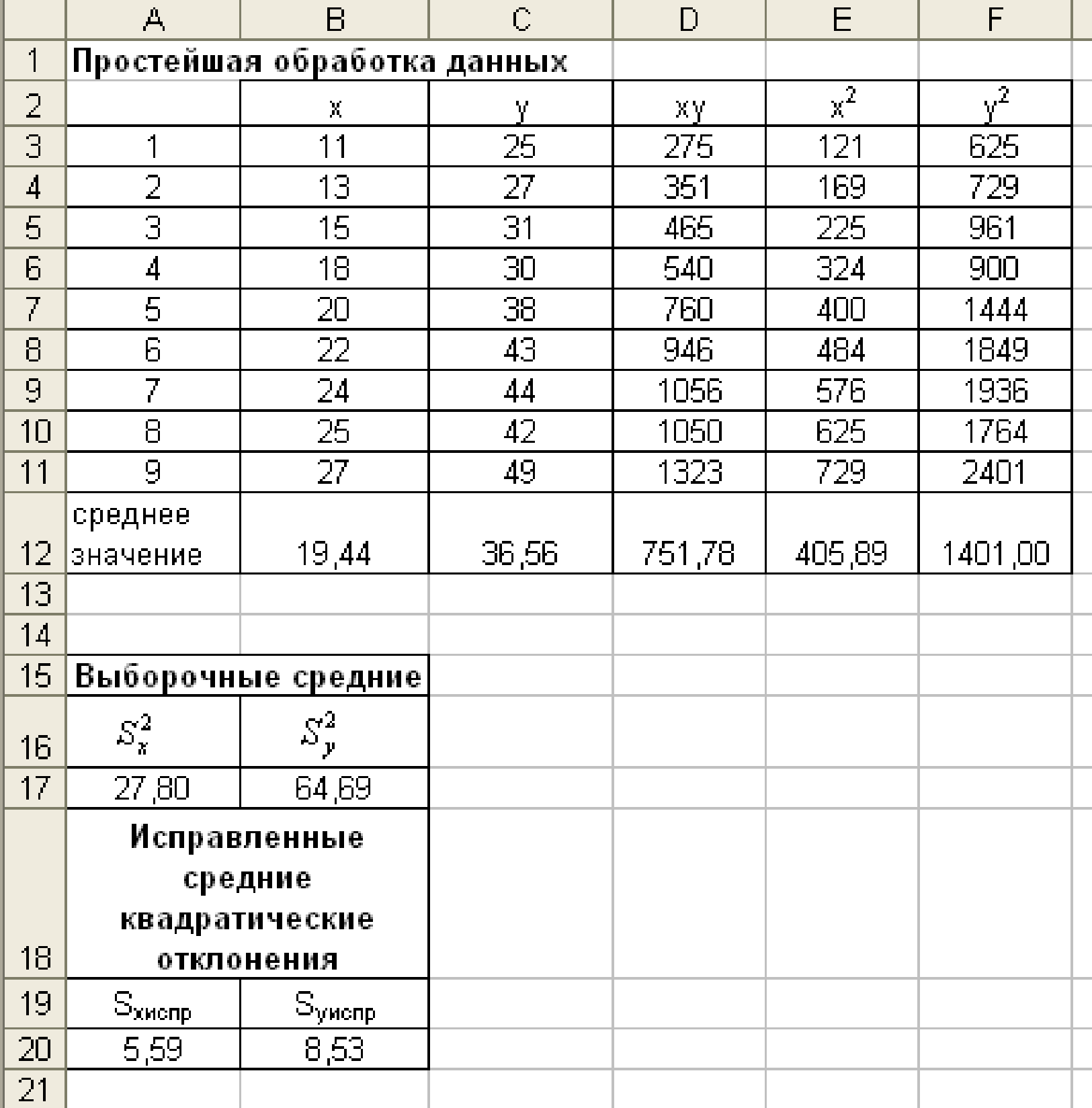


Рис. 1.1. Результаты простейшей обработки данных

3. Для определения коэффициента корреляции воспользуемся формулой 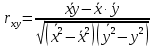. Для этого в ячейку Е16 вводим формулу =(D12-B12*C12)/КОРЕНЬ(A17*B17)

Из расчетов следует, что коэффициент корреляции r=0,97. Это свидетельствует о том, что связь между объемом выпуска продукции и численностью занятых весьма высокая и положительная.

4. Для проверки значимости коэффициента корреляции введем вспомогательные данные:

Ячейки

К16 9 число предприятий;

К17 0,05 уровень значимости.

5. Далее вводим следующие формулы:

Н19	=КОРЕНЬ((1-E16*E16)/(K16-2))	Стандартная ошибка
Н20	=E16/H19	t-статистика
Н21	=СТЬЮДРАСПОБР(K17;K16-2)	Критическое значение t-статистики
Н22	=ЕСЛИ(ABS(H20)>H21;"Значим";"Незначим")	Вывод

Таким образом, получим данные, представленные на рис. 1.2.



Рис. 1.2. Анализ значимости коэффициента корреляции

6. Для определения коэффициентов уравнения линейной регрессии на основе формул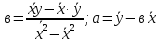



следует в ячейки I3, I4 ввести соответственно следующие формулы: =(D12-B12*C12)/A17;

=C12-I3*B12.

Уравнение регрессии у=7,9+1,47х.

Значение коэффициента b=1,47 говорит о том, что при увеличении численности занятых на 1 тыс.чел. объем продукции увеличится на 1,47 тыс.ед.

Результаты расчетов приведены на рис.1.3.



Рис. 1.3. Результаты расчетов

7. Для построения графика выделим диапазон В3:С11. Вызовем Мастер диаграмм. Чтобы ось отражала фактические данные, выберем тип диаграммы Точечная. После чего нажмем кнопку Готово. На построенной диаграмме выделим график функции, щелкнув по нему левой кнопкой мыши. Выделение обозначается светлыми маркерами на функции. Нажав правую кнопку мыши, выведем контекстно-зависимое меню, в котором выберем опцию Добавить линию тренда. В окне Линия тренда по вкладке Тип выберем тип функции Линейная, а во вкладке Параметры – установим флажок показывать уравнение на диаграмме. В результате на диаграмме появиться вид теоретической кривой – тренда и ее уравнение (рис.1.4).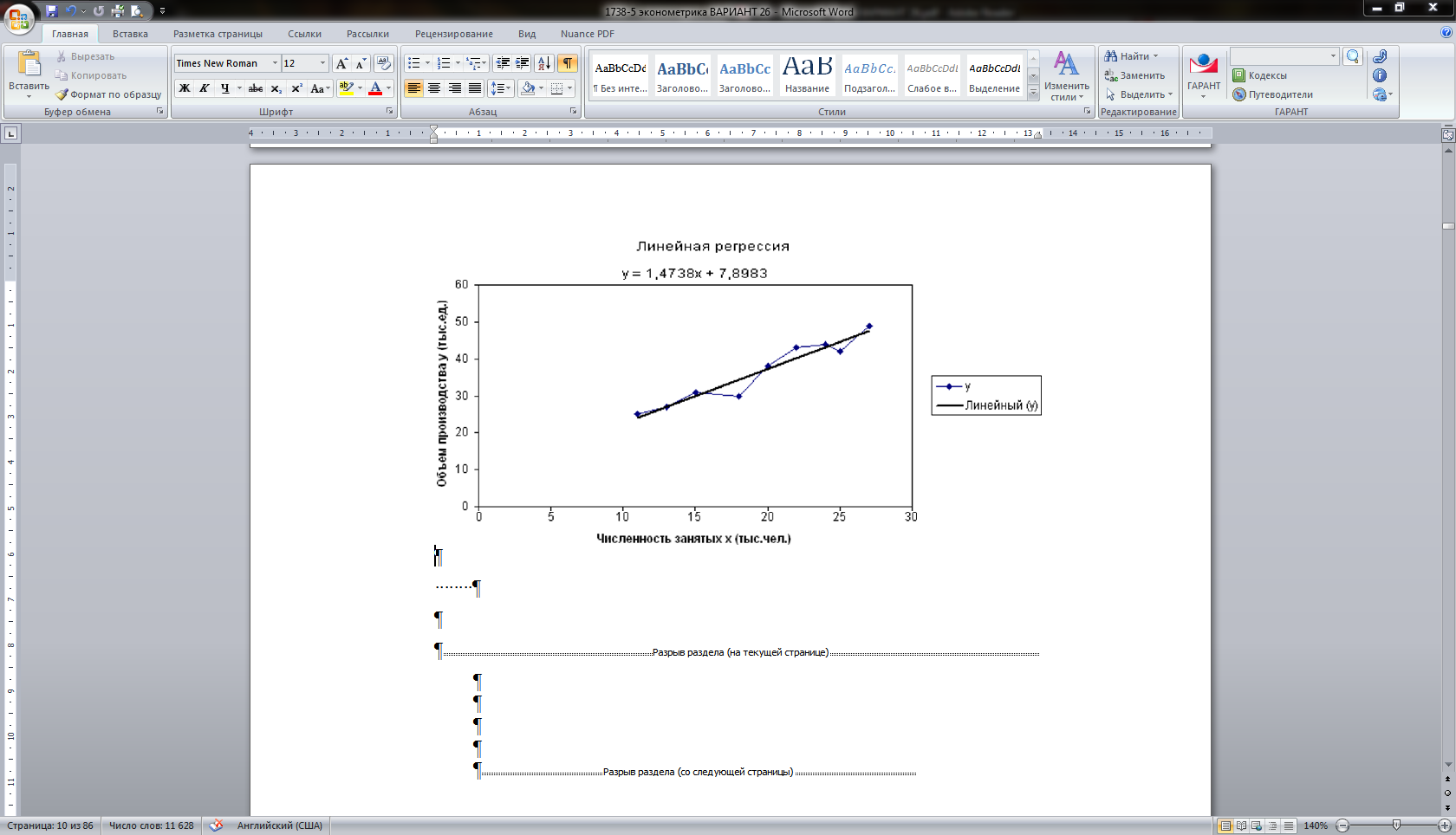



Рис. 1.4. Графики фактических данных и построенной регрессии
8. Вычисление параметров регрессии с помощью статистических функций Excel:

КОРРЕЛ(массив1;массив2) вычисляет коэффициент корреляции между двумя переменными; значения первой из них приведены в диапазоне массив1, значения второй – в диапазоне массив2;

НАКЛОН(известные_значения_y;известные_значения_х) служит для определения коэффициента b;

ОТРЕЗОК(известные_значения_y;известные_значения_х) служит для определения коэффициента а.

Вводим формулы:

С27	=КОРРЕЛ(B3:B11;C3:C11)	Коэффициент корреляции
С28	=НАКЛОН(C3:C11;B3:B11)	Коэффициент b
С29	=ОТРЕЗОК(C3:C11;B3:B11)	Коэффициент а

Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии. Порядок вычислений следующий:

1. 
   выделите область пустых ячеек 5х2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики (А27:В31);
   
2. 
   в главном меню выберите Вставка/Функция;
   

1. 
   
   
   
   в строке Категория (рис.1.5) выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните ОК.
   

Рис. 1.5. Диалоговое окно «Мастер функций»
4) Заполните аргументы функции (рис.1.6.):

Известные_значения_y – диапазон, содержащий данные результативного признака;

Известные_значения_x – диапазон, содержащий данные факторов независимого признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0.

Статистика – логическое значение, которое указывает выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводится только оценки параметров уравнения. Далее ОК.



Рис.1.6. Диалоговое окно ввода аргументов функции ЛИНЕЙН

5) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL+SHIFT+ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента а
Среднеквадратическое отклонение b	Среднеквадратическое отклонение а
Коэффициент детерминации R2	Среднеквадратическое отклонение у
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов.

Результаты регрессионного анализа представлены на рис.1.7.


Рис. 1.7.Результаты регрессионного анализа

Отчет по заданию

Используя данные из приложения 1, требуется:

1. 
   Запишите уравнение линейной парной регрессии для своего варианта и поясните экономическую сущность параметров уравнения.
   
2. 
   Что является показателем тесноты связи в парной линейной регрессии?
   
3. 
   Каково значение коэффициента корреляции?
   
4. 
   Каково значение коэффициента детерминации и что он характеризует?
   
5. 
   Как оценивается значимость коэффициента корреляции?
   
6. 
   Является ли коэффициент корреляции для вашего варианта значимым и почему?